Decimal numbers are numbers written in decimal notation. They are a very common way of writing fractions in a compact manner. You will encounter them everywhere in your daily life: on price tags, sizes, or on the display of your calculator.
In this article, you learn how you can put decimal fractions into place value charts or convert them into ordinary fractions.
Structure of decimal numbers
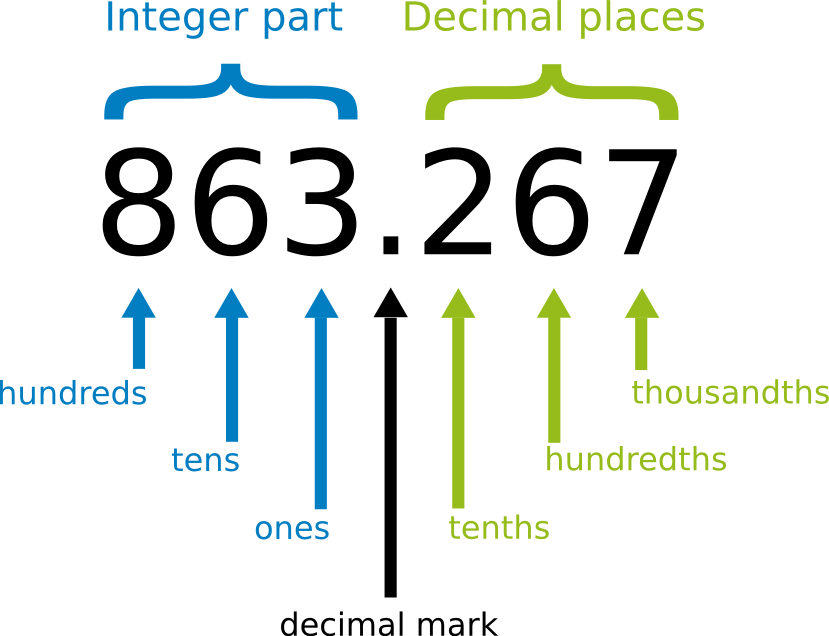
Every decimal numbers constructed in the following way: integer - decimal mark - decimal places:
The decimal mark - written like a full stop - separates the integer part from the decimal places.
In front of the decimal mark the integer part is written. (Ones, tens, hundreds etc.)
After the decimal mark the decimal places are written. (tenths, hundredths, thousandths etc.)
The decimal number shown in the figure will look like this when written in detail:
Decimal numbers in everyday life
You may encounter decimal numbers very often in everyday life, for instance if you want to buy something and look at the price tag.
Actually, decimal numbers work a bit like currencies: The number to the left of the decimal mark is "worth 1", just like a $1-bill.
The tenths digit is "worth 0.1" and works like a 10 cent coin. You need 10 of them to get a $1-bill.
The hundredths digit is "worth 0.01" and works like a 1 cent coin. You need 10 of them to get a 10 cent coin.
However, unlike currencies, there are also smaller units available given by the further digits, which are worth 0.001, 0.0001 and so on.
Decimal numbers in the place value chart
You may representing decimal numbers within a place value chart. To do so, you break down the number into its digits, corresponding to ones, tens, hundreds and so on.
The columns are accordingly labelled Th (thousands), H (hundreds), T (tens) and O (ones).
Perhaps the following picture will help to visualise the meaning of decimals: Imagine a one (O) as a single coin and a ten (T) as a bag which contains 10 coins. A hundred (H) is then a bag that contains 10 bags of tens (T). So in total, an (H) contains 100 coins.
For instance, the number 207 is composed of 2 hundreds, 0 tens and 7 ones. In the place value chart, it looks like this:
Th | H | T | O |
|---|---|---|---|
0 | 2 | 0 | 7 |
You may now extend this representation to numbers smaller than 1.
To do so, you add new digits on the right of the chart:
the tenth or , abbreviated as t
the hundredth or , abbreviated as h
the thousandth or , abbreviated as th.
In principle, you could add even more of them, depending on how many you need. For us, three digits will be OK for the moment. The extended place value chart now looks as follows:
Th | H | T | O | . | t | h | th |
|---|---|---|---|---|---|---|---|
0 | 0 | 0 | 0 | . | 0 | 0 | 0 |
To represent decimal fractions, the number is again split into its digits. As an example, let us consider the decimal fraction 1.83. This number can be split into
Th | H | T | O | . | t | h | th |
|---|---|---|---|---|---|---|---|
0 | 0 | 0 | 1 | . | 8 | 3 | 0 |
Since there is no thousandth in , you put a 0 into the t column.
Decimal numbers and fractions
Note that you can also write any decimal number as a fraction.
For instance, the decimal number0.1 can be written in different ways:
1 tenths, i.e., or
10 hundredths, i.e., or
100 thousandths, i.e.,
Does it make a difference whether we write or or even ? To see this, let's look at decimal fractions as fractions:
The fractions are identical, since you can shorten and to , respectively. Therefore, the decimal numbers and and are identical.
Now, how do you transform a decimal number into a fraction?
First, we start with the number to the left of the decimal mark, which represents an integer number.
The first digit after the decimal mark indicates how many tenths (t) are added to the integer. Each tenth corresponds to .
The second digit after the decimal mark indicates how many hundredths (h) are added to the integer. Each hundredth corresponds to .
The third digit after the decimal mark indicates how many thousandths (th), corresponding to are added to the integer, and so on...
We will consider the number 5.086 as an example.
The integer is 5. Then, the decimal mark is followed by 0 tenths (t), 8 hundredths (h) and 6 thousandths (th), i.e.
Periodic and non-periodic decimal numbers
You may distinguish between terminating and periodic decimal numbers. A terminating decimal numbers corresponds to a fraction whose denominator is a product of 2 and/or 5 or powers thereof. The number then terminates after finitely many digits.
By contrast, a periodic decimal number contains infinitely many digits, where a certain block will repeat infinitely often.
How to pronounce decimal fractions
In everyday life, when you pay at the checkout, you say, for example, "three dollars ninety-eight". This is because there are 98 cents in addition to the 3 dollars. There is a preference for spelling out the number of hundredths, since a hundredth of a dollar (= 1 cent) is a currency sub-unit.
However, in mathematics, all decimal places (tenths, hundredths, thousandths) are treated equally, so you spell out each digit separately. For instance, is mathematically pronounced as "three point nine eight dollars".
Still want more?
You can find more content on this topic here:
