If a decimal number has a lot of decimal places and thus becomes unwieldy, one often uses a rounded value instead of the exact number.
Example:
if we want to round the number to two decimal places.

(The symbol means "is approximately equal")
Basic principle
When rounding, the original "long" decimal number with many decimal places is replaced by a "shorter" number with fewer decimal places. This is done such that the shorter number has approximately the same value as the long number.
While rounding, you make sure that the rounded (short) number is as close as possible to the original (long) number. Just "truncating" the decimal number (dropping decimal places) does not suffice.
Example:
rounded to the first decimal place is and not , because is closer to than to .
Procedure
Step 1
Identify how many decimal places the resulting, rounded number should have.
Rounding to the nearest integer means that the rounded number does not have any decimal places left.
Rounding to the nearest tenth means that the rounded number has one digit after the decimal mark.
Rounding to the nearest hundredth means that the rounded number has two digits after the decimal mark.
Rounding to the nearest thousandth means that the rounded number has three digits after the decimal mark.
and so on...
Step 2
Separate the number into two parts:
The first part includes everything up to and including the digit to which the number should be rounded.
Everything afterwards constitutes the second part.
Example:
To round to the nearest hundredth, you need to split the number after the second decimal place:
Step 3
Look at the first digit of the second part of the number (the decimal place immediately after the one to which the number should be rounded.
If this digit is a or you need to round down - the rounded number is the same as the first part of the original one.
Example:
Rounding to the nearest thousandth yields the number because the digit after the third decimal place is a .
If this digit is a or you need to round up by increasing the last digit of the first part of the number by . (If the last digit was a before rounding, you need to adjust the other decimal places accordingly)
Examples
Rounding to the nearest tenth yields .
Rounding to the fourth decimal place yields .
Rounding to the nearest thousandth yields - in this example, multiple decimal places need to be adjusted.
Rounding to the nearest hundredth yields .
Rounding to integers
Rounding to integers means finding the integer that is closest to the given decimal number. If the decimal number is an integer, then the closest integer is the integer itself.
You round down if the digit before the decimal point (tenth) is between 0, 1, 2, 3 or 4.
You round down if the digit before the decimal point (tenth) is between 5, 6, 7, 8 or 9.
Examples in the place value chart
O | t | h | |
|---|---|---|---|
decimal number | 0. | 7 | 3 |
decimal number | 1. | 2 | 6 |
rounded number | 1. | 0 | 0 |
0.77 is rounded to 1 because the tenth digit is a 7.
1.26 is rounded down to 1 because the tenth digit is a 2.
O | t | h | |
|---|---|---|---|
decimal number | 1. | 5 | 0 |
rounded number | 2. | 0 | 0 |
1.5 is rounded up to 2 because the tenth digit is a 5.
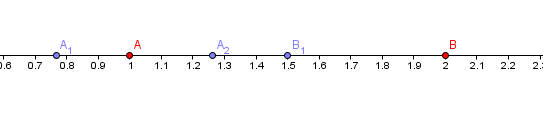
Examples on the number line
and are rounded to , is rounded to .
Calculation examples
Because the tenths digit 3 lies between 0 and 4, it is rounded down,
i.e. the 2 is left standing.
Because the tenths digit 7 lies between 5 and 9, it is rounded up,
i.e. the 3 becomes the 4.
Because the tenths digit 4 lies between 0 and 4, it is rounded down,
i.e. the 2 is left standing.
You must never round in two or more steps! Only one step is allowed.
For instance, the following two-step rounding would be wrong: .
The correct one-step rounding reads: .
Reasonable rounding
Frequently, you need to round without anyone telling you, to which digit. Often, this happens when calculating with units of measurement or currencies. So what is a reasonable choice for the digit you round to?
For currencies, it is common to round to integers (₹) or hundredths ( ), depending on what is the smallest amount that you can pay with coins.
For units of measurement, there are often several reasonable rounding options, depending on the situation. Typically, 2-3 digits in total are OK. If you need high-precision results, also 4 or even 5 diigits may be required. Sometimes, also 1 digit is OK for a rough estimate.
Sample task:
Peter drives 20 minutes by car. He consistently drives 100 km/h. How far did Peter drive? Round the result reasonably.
Solution:
20 minutes are hour. In one hour it covers 100 kilometers, so in hour kilometers. So there are infinitely many digits, down to meters, millimeters, nanometers, and so on. For long distances covered by car, it is not useful to specify the distance in millimeters or even more precise! Typically, it is OK to round to full kilometers, since this is how distances are indicated on road signs.
Peter has driven kilometers.
But depending on the situation, it would also be OK, to round to or or kilometers (if you really want to be precise) or to kilometers (as a rough estimate).
Exercises
You can find more exercises in the following folder::
Exercises: rounding decimal numbers
