Powers

Powers are a shortened notation for multiplying a number by itself several times.

Example: You may write $\underbrace{2\cdot2\cdot2}_{3~\text{factors}}$ as $2^3$ (with power 3).

The exponent, in this example $3$ , describes how often a number is multiplied by itself.

In general, any number without an exponent has automatically an exponent of 1 (beacuase if you multiply $x$ one time by itself, you exactly get $x$ ).

That is, $x=x^1$ .

The exponent is usually omitted in this case.

Example: $3^1=3$

If you exponentiate any number $x$ by $0$ , you always get $x^0=1$ . The only exception is $x=0$ . In some books, " $0^0$ " is not defined. In others, it is set $0^0=1$ . We will also adopt the convention $0^0=1$ .

Attention

The convention $0^0=1$ is a bit dangerous, since one could also argue that for any natural number $a$ , we have $0^a = \underbrace{0 \cdot \ldots \cdot 0}_{a \text{ times}} = 0$ . So there are also arguments to define that $0^0$ is equal to $0$ . However, this definition is usually not used.

Why do people like to set $0^0=1$ and not $0$ ?

If in more advanced mathematics, you want to write polynomials using summation signs, for example, for a third degree polynomial, then you get

\displaystyle a_3x^3+a_2x^2+a_1 x+a_0=\sum\limits_{n=0}^3 a_nx^n

Here, for $n=0$ the corresponding summand is $a_0x^0$ and should be equal to $a_0$ . In order for obtaining $a_0x^0 = a_0$ also for $x=0$ , it is convenient to set $0^0=1$ .

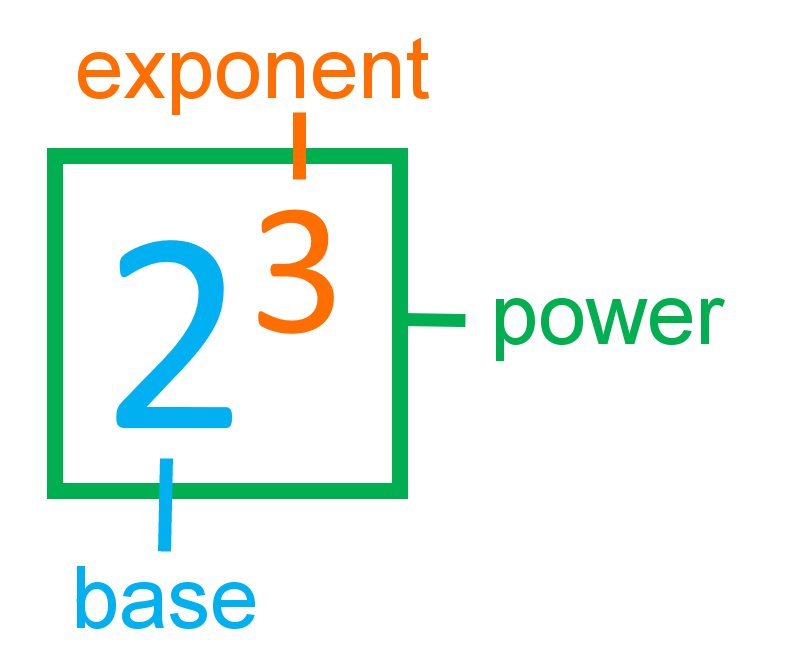
Base and exponent

The number to be multiplied by itself is called the base, the number of self-multiplications is called the exponent. Both together are called a power. If the exponent is $n$ , it is also common to speak of an " $n$ -th power" or to say that the base is taken "to the power $n$ " or "to the $n$ ".

Powers with negative base

If you take a power of a negative number, the result may be positive or negative:

If the exponent is even, then the result becomes positive.
if the exponent is odd, then the result stays negative.

Examples:

$\left(-2\right)^2=\left(-2\right)\cdot\left(-2\right)\ =\ +4\$

$\left(-2\right)^3=\left(-2\right)\cdot\left(-2\right)\cdot\left(-2\right)\ =\ -8$

Why is that the case?

Let's calculate $(-a)^b$ explicitly:

\displaystyle a_3x^3+a_2x^2+a_1 x+a_0=\sum\limits_{n=0}^3 a_nx^n

The term $a^b$ is positive because the number $a$ is greater than zero. For the term $(-1)^b$ , we can use that "minus times minus equals plus":

$(-1)^1 = (-1) = -1$

$(-1)^2 = (-1)\cdot (-1) = +1$

$(-1)^3 = (-1)\cdot (-1)\cdot (-1) = -1$

$(-1)^4 = (-1)\cdot (-1)\cdot (-1)\cdot (-1) = +1$

$\vdots$

So generally,

$(-1)^{\text{even number}}=1$

$(-1)^{\text{odd number}} = -1$

Now if $b$ is an even number, then $(-1)^b$ is positive, and if $b$ is an odd number, then $(-1)^b$ is negative. Thus, $(-1)^b\cdot a^b=(-a)^b$ is also positive if $b$ is even, and negative if $b$ is odd.

Powers with negative exponents

How can you interpret $a^{-x}$ ?

\displaystyle a_3x^3+a_2x^2+a_1 x+a_0=\sum\limits_{n=0}^3 a_nx^n

Why is that the case?

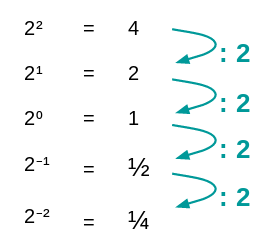
If the exponent is reduced by one, that means that the number is divided by the base. For positive exponents you already know this, and it is also true for negative exponents.

Here you see the division procedure for a general number $a$ . Starting from $a^0=1$ , after $k$ division steps, you will find the above formula.

Examples:

$2^{-1}=\dfrac12$

$4^{-2}=\dfrac1{4^2}=\dfrac1{16}$

$\frac{3}{25}=3\cdot\frac{1}{25}=3\cdot5^{-2}$

Rational Exponents

Numbers thathave a rational number (i.e., a fraction) as an exponent can be identified as a root:

\displaystyle a_3x^3+a_2x^2+a_1 x+a_0=\sum\limits_{n=0}^3 a_nx^n

Thus, for the "standard" square root:

\displaystyle a_3x^3+a_2x^2+a_1 x+a_0=\sum\limits_{n=0}^3 a_nx^n

Examples:

\displaystyle a_3x^3+a_2x^2+a_1 x+a_0=\sum\limits_{n=0}^3 a_nx^n

\displaystyle a_3x^3+a_2x^2+a_1 x+a_0=\sum\limits_{n=0}^3 a_nx^n

Calculating with powers

In the article Power Laws you can learn some useful rules that allow you to do calculations with powers.

Exercises

Content is loading…

You can find more exercises in the following folder::
Exercises: Simple fractions

This content is licensed under
CC BY-SA 4.0 → Info