Exercises: systems with two variables
- 1
Test your knowledge!
Put the steps of the equation system solving process in the correct order!
To do this, enter the numbers of the steps in the solution field one after the other without spaces (e.g. 123).
Plug the variable into an equation.
Set equal the equations and .
Solve the resulting equation for one variable.
Which of the following describes an intersection point?
What do you need llnear systems of equations for?
- 2
Solve the following systems of equations!
For this task you need the following basic knowledge: Elimination by equating coefficients
Solving linear systems by equating coefficients
1. solve both equations for y
Solve both equations for one variable. In this case, is already singled out, so it is easier to solve for .
2. Set equal
Equate and .
3. Solve equation for x
4. Plug in x to find y
Plug into or .
Write down the solution set.
For this task you need the following basic knowledge: Elimination by equating coefficients
Solving linear systems by equating coefficients
1. Solve both equations for x
Solve both equations for one variable. For example, for .
2. Set equal
Set equal and .
3. Solve for y
4. Plug in y to find x
plug into
Write down the solution set
For this task you need the following basic knowledge: Elimination by equating coefficients
Solving linear systems by equating coefficients
1. Solve both equations for one variable (for instance y)
2. Set equal
Set equal and .
3. Solve for that one variable
Solve for .
4. Plug into one equation to find the other variable
Plug into .
Now, you can write down the solution set again
- 3
Solve the linear systems of equations using the substitution method.
For this task you need the following basic knowledge: Substitution method
First you have to solve one of the two equations for one variable. In the present case you can see that equation is already solved for .
Plug from equation into
Multiply out the parenthesis and solve for .
Plug from into
And finally write down the solution set.
.
For this task you need the following basic knowledge: Substitution method
First you have to solve one of the two equations for or . It is, for instance, a good idea to solve equation for .
Solve equation for .
Plug from into
Multiply out the parenthesis and solve for .
Substitute into the transformed second equation to determine .
And finally, write down the solution set.
.
- 4
Solve the following system of equations using the addition method!
For this task you need the following basic knowledge: Addition method
Step 0: Tidying up the equations and selecting a variable
Since the equations are already nicely ordered this point is not needed.
In this case it is the same effort to solve the problem, no matter if you select or .
The solution is calculated for the variable .
Step 1: Multiply the equations
In equation there are , in equation there are . So a common multiple is . Multiply the first equation by and the second equation by .
Equation 1
Equation 2
Step 2: Elimination of a variable by addition/subtraction.
The signs of the selected variable are the same both times. Therefore you have to subtract.
Step 3: Determine the values of both variables.
Determine the value of
Determine the value of by plugging into
So the solution is given by and : .
- 5
Test your knowledge! Which method is useful to solve the following systems of equations?
For this task you need the following basic knowledge: System of linear equations
The equation is already solved for . Therefore, the substitution method is advisable.
The other two methods also get you to the goal, but they require further transformation steps.
For this task you need the following basic knowledge: System of linear equations
All three methods can be applied directly and are useful for this reason.
For this task you need the following basic knowledge: System of linear equations
Equation contains , equation contains . So the will drop out when adding both lines, which makes the addition method suitable.
With the other two procedures, you have to take further transformation steps, before one can apply them.
- 6
Solve with the most appropriate method.
For this task you need the following basic knowledge: System of linear equations
For this exercise, the addition method is most suitable, as occurs in both equations.
Solve for
Plug into one of both equations, for instance
Write down the solution set
For this task you need the following basic knowledge: System of linear equations
You get a very nice solution with the substitution method.
The equation is solved to and in equation there is . You can even use the substitution method without doing any transformation.
Transform equation
Plug from into
Conclude and solve for
As you can see now, the entries in the last line are not the same, which results in a contradiction. Hence, the system has no solution, since no number can be assigned for , such that is satisfied.
For this task you need the following basic knowledge: System of linear equations
You best use the addition method, since you can see with a sharp eye (this is what math lessons shall train you for) that is times .
Multiply the first equation by 4
As you can see now, both equations are identical. It follows that the system has an infinite number of solutions. Graphically, this corresponds to two straight lines lying on top of each other.
Solve the equation for one more variable to obtain the solution set.
- 7
Determine the solution sets of the following systems of equations.
For this task you need the following basic knowledge: System of linear equations
In this case, the substitution method is useful, since the second equation is already solved for one variable.
Plug equation into
Solve for y
Plug into and solve for x
For this task you need the following basic knowledge: System of linear equations
In this case, the substitution method is useful, since the second equation is already solved for one variable.
Plug equation into
Solve for
Plug into and solve for
For this task you need the following basic knowledge: System of linear equations
In this case, the substitution method is useful, since the second equation is already solved for one variable.
Plug equation into
Solve for
Plug into and solve for x
For this task you need the following basic knowledge: System of linear equations
In this case, the substitution method is useful, since the second equation is already solved for one variable.
Divide by 2 and solve for
Plug into
plugged into :
Then, solve for
Finally, plug into and solve for
plugged into :
Alternative solution: equating coefficients
Another option is to use the method of equating coefficients, because on the left side of and on the right side of there is almost the same term.
Multiply by to get a on the right hand side.
Set the right side of equal to the left side of and solve for .
Plug into (or ) and solve for .
Alternative solution: combining addition and substitution method
The addition method can also be used here. To apply it, the equations are first transformed, so that the appropriate terms are placed one below the other:
Subtract the second equation from the first equation.
Since the first equation is now solved for , we can use the substitution method again.
Plug into and solve for .
Plug into and solve for .
- 8
Solve the following systems of equations with 2 equations and 2 variables first graphically and then by computation.
For this task you need the following basic knowledge: System of linear equations
Linear system with two variables
A linear system of equations is composed of several linear equations with common unknowns (variables), all of which are to be satisfied.
Graphical solution
To solve the system of equations graphically, you can resolve the individual lines for and draw the corresponding lines into a coordinate system. Then you only need to read off the coordinates of the intersection of the two lines.

The intersection point is at and . Thus the solution set is .
Solution by computation
In this case, the elimination by equating coefficients is a good choice, since you have already solved both equations for in order to solve them graphically.
Set and equal and solve for .
Plug the obtained value for into one of the equations, e.g. .
Now, you can write down the solution set.
For this task you need the following basic knowledge: System of linear equations
Linear system with two variables
A linear system of equations is composed of several linear equations with common unknowns (variables), all of which are to be satisfied.
Graphical solution
To solve the system of equations graphically, you can resolve the individual lines for and draw the corresponding lines into a coordinate system. Then you only need to read off the coordinates of the intersection of the two lines.

The intersection is at and . Thus the solution set is .
Solution by computation
In this case, the elimination by equating coefficients is a good choice, since you have already solved both equations for in order to solve them graphically.
Set and equal and solve for .
Plug the obtained value for into one of the equations, e.g. .
Now, you can write down the solution set.
For this task you need the following basic knowledge: System of linear equations
Linear system with two variables
A linear system of equations is composed of several linear equations with common unknowns (variables), all of which are to be satisfied.
Graphical solution
To solve the system of equations graphically, you can resolve the individual lines for and draw the corresponding lines into a coordinate system. Then you only need to read off the coordinates of the intersection of the two lines.
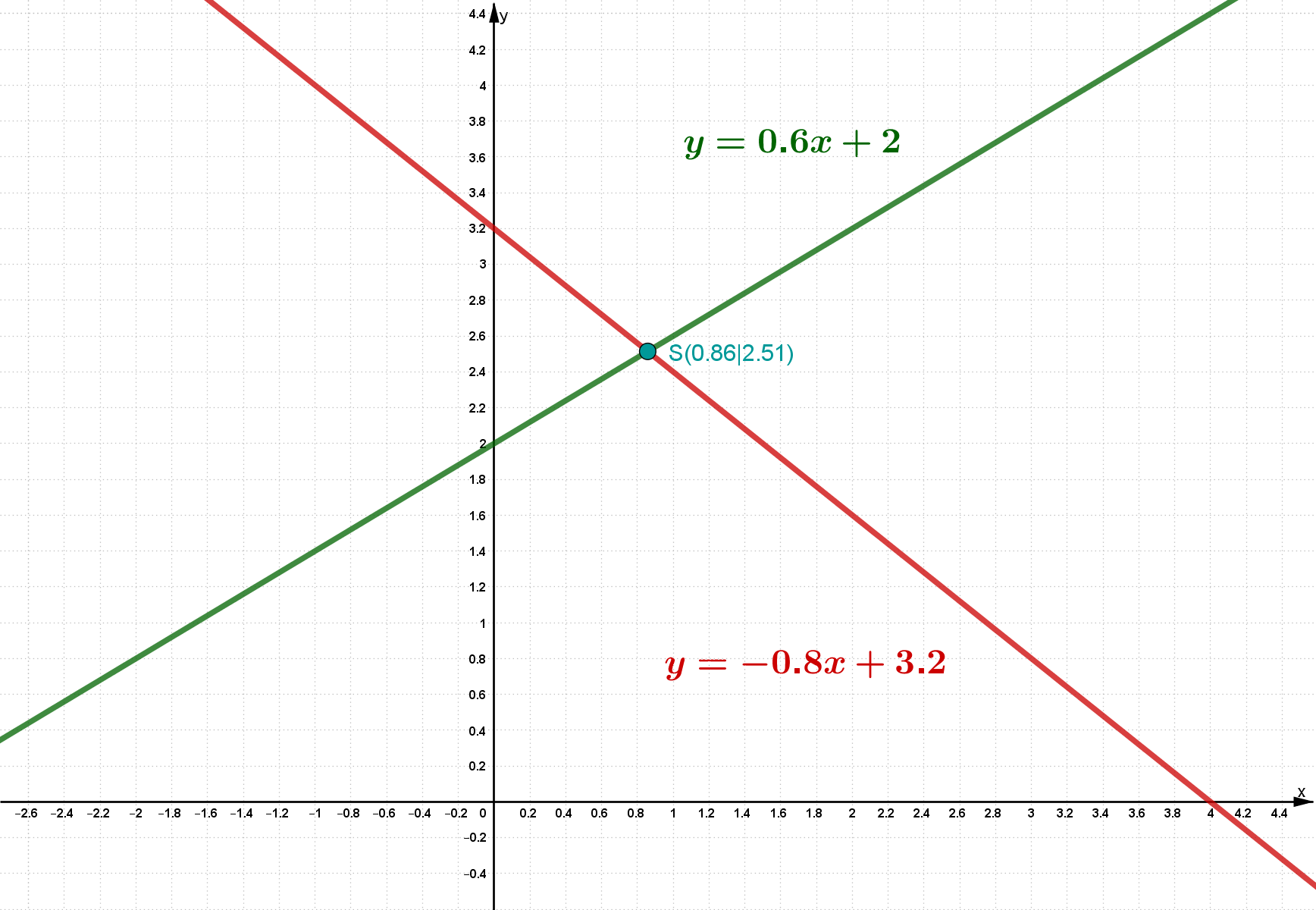
The intersection is at and . Thus the solution set is .
Solution by computation
In this case, the elimination by equating coefficients is a good choice, since you have already solved both equations for in order to solve them graphically.
Set and equal and solve for .
Plug the obtained value for into one of the equations, e.g. .
Now, you can write down the solution set.
- 9
Test your knowledge!
Which of the following is a system of linear equations? Check all the answers that apply.
For this task you need the following basic knowledge: System of linear equations
We have a linear system of equations if and only if:
We have several equations that have to be fulfilled at the same time.
Those equations are linear, that means every variable occurs at most with power 1
Now, let's check:
Is not a linear system, since and have power in the first line.
Is not a linear system, since has power in the second line.
All other systems are indeed linear, since and only appear with power .
How many solutions has the following linear system of equations?
For this task you need the following basic knowledge: Solvability of linear systems
You may show that the equations and cannot be satisfied at the same time. The best way to do this is by subtraction.
Subtract equation from .
The equation is obviously wrong. Thus, the given system of equations is also "wrong" and has no solution.
Thus the solution set is .
How many solutions does the following system of equations have?
For this task you need the following basic knowledge: Solvability of linear systems
You need to show that equations and are equivalent. That is, any and that solves equation also solves equation (and vice versa).
One way to show this is by the substitution method.
First, solve for y .
Now substitute into equation . You get the new equation .
Summarize the left side of the equation.
The equation is true and independent of . So there are infinitely many solutions.
How many solutions does the following linear system of equations have?
For this task you need the following basic knowledge: Solvability of linear systems
A linear system of equations has exactly one solution, if it can be solved unambiguously for and .
In order to find this out, the substitution method is useful, because for example equation can be solved for very easily.
First solve equation for .
Now plug into . You get the new equation .
Summarize the left side.
Solve for .
Plug into , in order to get .
Solve for .
So there is exactly one solution.
- 10
Determine the solution sets of the following systems of linear equations.
For this task you need the following basic knowledge: System of linear equations
You can solve linear systems of equations using the substitution method, the addition method, or by equating coefficients.
The substitution method is best suited here.
Substitution method
Given is:
Equation is solved for . This term also appears in equation . So plug equation into .
↓ from eq , plug in
↓ multiply out the bracket
↓ solve for
To find , plug the value of into .
↓ plug in
Write down the solution set.
Solution by other methods
For this task you need the following basic knowledge: System of linear equations
You can solve linear systems of equations using the substitution method, the addition method, or by equating coefficients.
The substitution method is best suited here.
Substitution method
Given is:
Rewrite such that is on one side.
Plug into and solve for .
↓ plug in
↓ compute the fractions
plug into .
↓ plug in
Write down the solution set, first the solution for , then for .
Solution by other methods
- 11
A hotel has 105 beds, which are located in 40 two- and three-bed rooms. How many two-and-three-bed rooms does the hotel have?
Solve the problem by using a system of equations!
For this task you need the following basic knowledge: System of linear equations
Extracting equations from the problem setting
What is known? The sum of the number of two-bed rooms and the number of three-bed rooms is 40. This statement gives you equation :
In a double room there are two beds. Thus, there are beds in two-bed rooms and correspondingly, there are beds in the three-bed rooms. In total, the hotel has 105 beds, so you can set up equation :
You have now obtained the following system of linear equations with two equations and two unknowns:
Solve the system
To solve this system of equations, you have three solution methods at your disposal:
Solving by substitution method
Solve equation for one of the two variables and substitute this variable into equation . It doesn't matter whether you solve for or .
. plugged into
Plug into equation :
So the solution set of the linear system is :
Answer: The hotel has 15 two-bed rooms and 25 theree-bed rooms.
Solving by equating coefficients
Solve both equations for the same variable. You have already solved the equation for in the substitution method:
. Now, also must be solved for :
Now set equal the two right sides of the equations and :
Plug into :
So the solution set of your system of equations is :
Answer: The hotel has 15 two-bed rooms and 25 theree-bed rooms.
Solvin by the addition method
The goal is that by adding the two equations, one of the unknown variables cancels out. In this system of equations you can, for instance, multiply equation by , which gets you . By adding and , you get the solution for :
Plug into :
So the solution set of the linear system is :
Answer: The hotel has 15 two-bed rooms and 25 theree-bed rooms.
Construct a linear system of equations from the problem setting.
Tip: Choose the variable for the number of two-bed rooms and the variable for the number of three-bed rooms.
- 12
A farmer keeps chickens and rabbits in his barn. He counts a total of 120 legs. There are three times more chickens than rabbits. How many chickens and rabbits does the farmer have?
Solve by suing a system of equations!
For this task you need the following basic knowledge: System of linear equations
Transforming the problem setting into equations
You may denote the number of chickens by some variable and the number of rabbits by a variable . What is known? A chicken has two legs, a rabbit has four legs. Thus chickens have legs and rabbits have legs. This statement gives you equation :
"There are three times more chickens than rabbits" must also be cast into an equation. Since is the number of rabbits, you must multiply by to get the number of chickens. So equation reads:
You have now obtained the following system of linear equations with two equations and two variables:
To solve this system of equations, you have three methods at your disposal:
Here the substitution method is suitable, since the equation is already solved for .
Solution by substitution
Plug equation into :
Plug into equation :
So the solution set of your system of equations is :
Answer: The farmer has chickens and rabbits.
When solving systems of equations, a verification is useful at the end of the calculation. In this case: chickens have legs and rabbits have legs. The sum of the legs is , as indicated in the problem setting. The number of chickens was supposed to be three times the number of rabbits. This statement is also correct, since . So the given solution set is indeed a solution of the linear system.
Construct a linear system of equations from the problem setting.
Hint: Choose the variable for the number of chickens and the variable for the number of rabbits.
- 13
Determine the solution sets of the following systems of nonlinear equations.
where
For this task you need the following basic knowledge: System of linear equations
You may solve linear systems of equations using the substitution method, the addition method or by equating coefficients. Such methods can also be effective for some non-linear system of equations.
Here the addition method is suitable. If you transform the two equations so that the terms with or are identical, you can subtract the two transformed equations from each other and only have to solve one equation with one variable.
Solution by addition method
Using the addition method you get to the following solution:
Given is:
The equation contains a term and equation is a multiple of , namely . So you can multiply by and add both equations to eliminate .
So the new system of equations is:
:
Now solve the new equation for .
↓ invert the fractions
Now, plug into one of the above equations, e.g. , and solve for .
↓ plug in
Write down the solution set. .
Try to solve these non-linear equations using the methods you already know for linear systems of equations.
where
For this task you need the following basic knowledge: System of linear equations
You may solve linear systems of equations using the substitution method, the addition method or by equating coefficients. Such methods can also be effective for some non-linear system of equations.
Here the addition method is suitable. If you transform the two equations so that the terms with or are identical, you can subtract the two transformed equations from each other and only have to solve one equation with one variable.
Solution by the addition method
Using the addition method you get to the following solution:
Given is:
Transform such that on one side you have only variables and on the other side only numbers.
The new system of equations is now:
Now, equation contains the term and equation is a multiple of , namely . So you multiply by and add both equations in order to eliminate .
:
Now, you solve , by inverting the fraction.
↓ shorten
Now, plug into one of the above equations, for instance , and solve for .
↓ plug in
↓ invert the fraction
Write down the solution set.
Try to solve these non-linear equations using the methods you already know for linear systems of equations.
where and
For this task you need the following basic knowledge: System of linear equations
This non-linear system of equations can be transformed into a linear system of equations. And you may solve linear systems using the substitution method, the addition method or by equating coefficients.
Given is:
Transform and , such that both equations no longer contain a fraction.
↓ multiply by the denominators
↓ multiply by the denominators
Thus, the linear system of equations is:
Now you can use the known procedures for solving the system of equations.
Solution by the substitution method
With the substitution method you get this solution:
Given is:
Transform , such that appears only one one side.
Plug into .
↓ plug in
↓ Solve for
Plug into , in order to find .
↓ plug in
Write down the solution set.
Additionally: Check your solution
Plug and into equations and and check if the equation is satisfied.
↓ plug in and
↓ plug in and
Both equations are satisfied, so our solution is correct.
Try to solve these non-linear equations using the methods you already know for linear systems of equations.
where and
For this task you need the following basic knowledge: System of linear equations
You may solve linear systems of equations using the substitution method, the addition method or by equating coefficients. Such methods can also be effective for some non-linear system of equations.
Here the addition method is suitable. If you transform the two equations so that the terms with or are identical, you can subtract the two transformed equations from each other and only have to solve one equation with one variable.
Solution using the addition method
Given is:
The equation contains the term and contains a multiple of , namely . So you multiply by and add both equations in order to eliminate .
So the new system of equations is:
:
Now solve the equation resulting from the addition for .
↓ invert the fractions
Now, plug into one of the above equations, e.g., , and solve for .
↓ plug in
↓ invert the fractions
Write down the solution set, using first the solution for , then for .
Try to solve these non-linear equations using the methods you already know for linear systems of equations.