Applications of linear systems
- 1
There are 30 children at a birthday party.
You know that there are four times as many girls as boys.
How many girls and how many boys are on the party?
Solve with a system of equations!

- 2
Mick and Max go shopping. Mick buys chocolate bars and ice creams and pays , Max buys a chocolate bar and ice creams for .
Now, Stephen drops by with . Can he buy an ice cream with that?

- 3
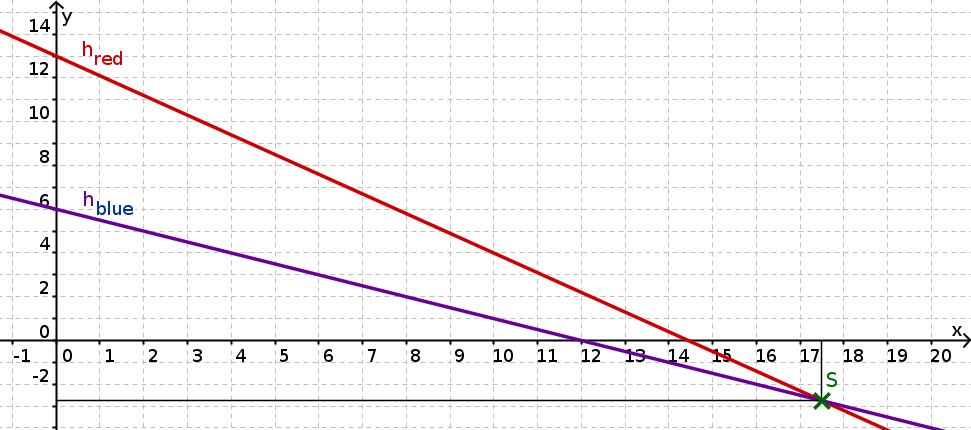
Two burning candles

Here, you can see two candles, which burn down slowly. Since the red candle is much thinner than the blue one, it will burn down faster. At the beginning, the blue candle is tall, and the red one is tall. By watching similar candles of the same kind, you know already that in one hour, the blue one burns down by and the red one by .
Write down a function equation for each of the two candles that represents its height as a function of time . So you end up with two equations.
Now, compute after how many hours the candles will be the same length by turning the two functions into equations with the variables and .
The result from b) is not very realistic. Do you know, why?
- 4
Dave once filled up his bike with a mixture of premium and regular gasoline. He paid in total for gallons of this mixture.
How many gallons of each type did he load if gallon of premium gasoline is and 1 gallon of regular gasoline is ?
Set up a system of equations from the given information.
Solve the system of equations using the equation method. Do only consider numbers and not their meanings.
What does the numerical solution in b) tell us about the solution of the original problem (with gallons and dollars)?
- 5
Your friend buys a wild mix of hamburgers and cheeseburgers at a fast food restaurant. The number of all burgers is and together they cost \$ 12.68 .
You also know taht a hamburger costs and a cheeseburger .
Using the information from the text, set up a system of linear equations.
Show that hamburgers and cheeseburgers is a solution to the system of equations.
Why is there exactly one solution?
- 6
Father and son are 34 years old together. How old is each of them if the difference in their ages is 26 years?