Trigonometry on the unit circle

If you apply the angle $α$ to the $x$ -axis, you can read off the values of the sine and cosine of $α$ on the unit circle.

If you look at the right triangle with angle $α$ in the unit circle, the hypotenuse has length $1$ :

$\cos (α) = adjacent cathetus$
$\sin (α) = opposite cathetus$

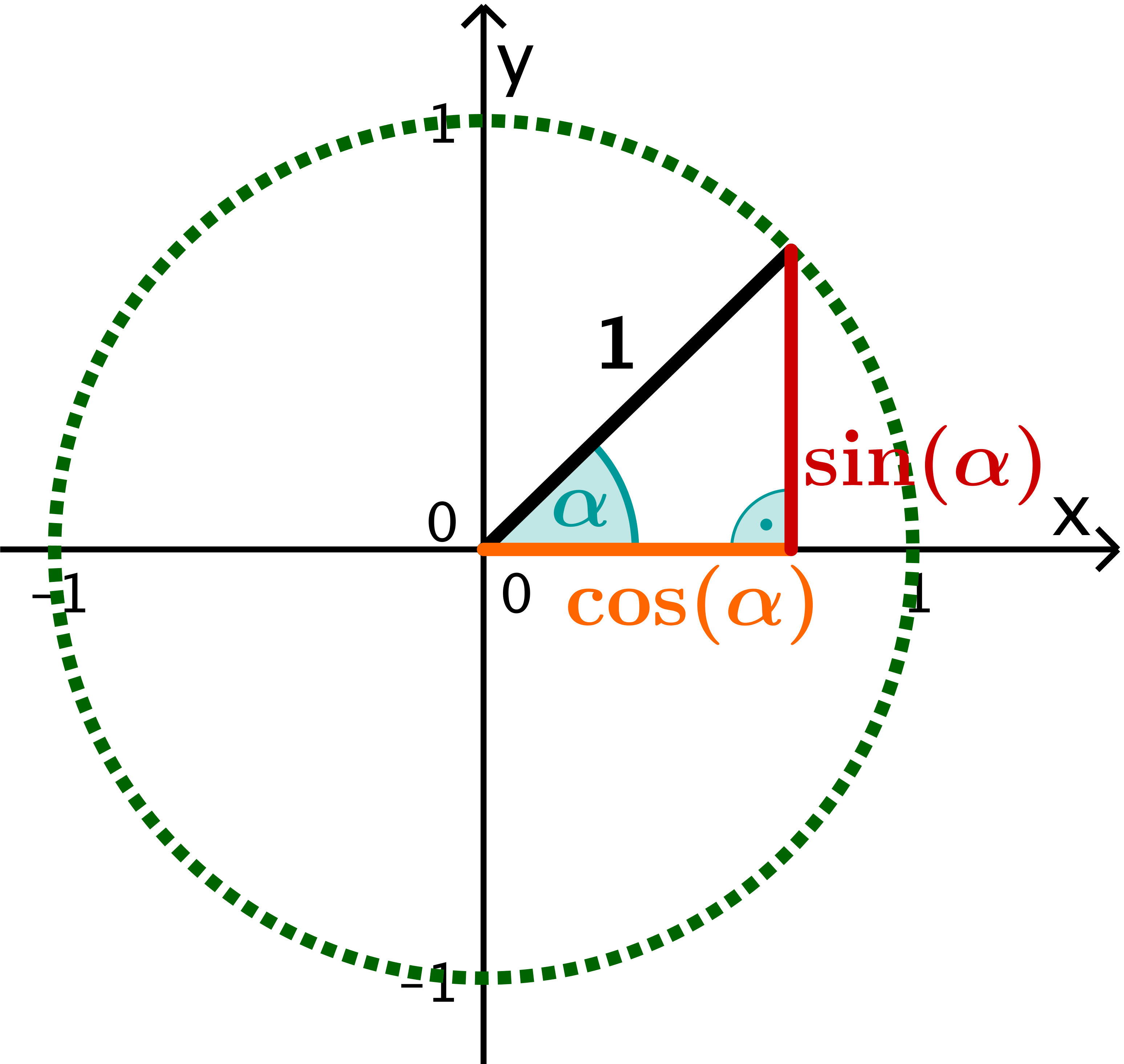
Presign

The trigonometric functions can change their sign when passing from one quadrant to the next. The change is illustrated in the following graphs.

Sine

Cosine

Tangent

Important values

The table below lists some important values for the trigonometric functions. For the first five values of the sine and cosine, there is an easy way to remember the values. They have the general form $\frac{1}{2} \sqrt{n}$ , where you put the numbers $0$ to $4$ in ascending order for the sine and in descending order for the cosine.

Angle	$0 °$	$30 °$	$45 °$	$60 °$	$90 °$	$180 °$	$270 °$	$360 °$
$\sin (α)$	$\frac{1}{2} \sqrt{0} = 0$	$\frac{1}{2} \sqrt{1} = \frac{1}{2}$	$\frac{1}{2} \sqrt{2}$	$\frac{1}{2} \sqrt{3}$	$\frac{1}{2} \sqrt{4} = 1$	$0$	$- 1$	$0$
$\cos (α)$	$\frac{1}{2} \sqrt{4} = 1$	$\frac{1}{2} \sqrt{3}$	$\frac{1}{2} \sqrt{2}$	$\frac{1}{2} \sqrt{1} = \frac{1}{2}$	$\frac{1}{2} \sqrt{0} = 0$	$- 1$	$0$	$1$
$\tan (α)$	$0$	$\frac{\sqrt{3}}{3}$	$1$	$\sqrt{3}$	$*$	$0$	$*$	$0$

$*$ : At these points the tangent does not exist, because the tangent is defined as "sine over cosine" and at these points the cosine is equal to zero.

Visualization by an applet

By clicking on image or button above you agree that external content from GeoGebra will be loaded. Also personal data may be transferred to this service in accordance with our privacy policy.

Video about the tangent on the unit circle

Exercises

This content is licensed under
CC BY-SA 4.0 → What does that mean? serlo.org