Quadratic Function

A quadratic function is a polynomial of the second degree, i.e. a function of the form: $𝒇 (𝒙) = 𝒂 𝒙^{𝟐} + 𝒃 𝒙 + 𝒄$ with $\begin{array}{l} a \neq 0 \end{array}$

Graph

The graph of a quadratic function is always a parabola.

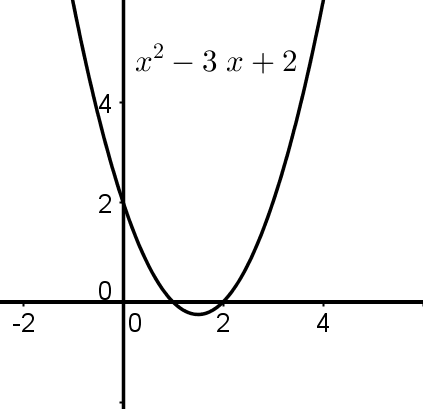
Zeros

Quadratic functions are polynomials of the second degree and therefore have at most two real zeros.

The number of zeros is given by the discriminant $D = b^{2} - 4 a c$ of the function:

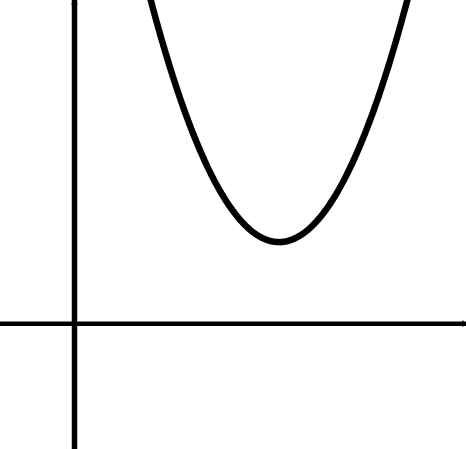
For $D < 0$ , the quadratic function has no zero.

For $D = 0$ , the quadratic function has exactly one zero.

For $D > 0$ , the quadratic function has two zeros.

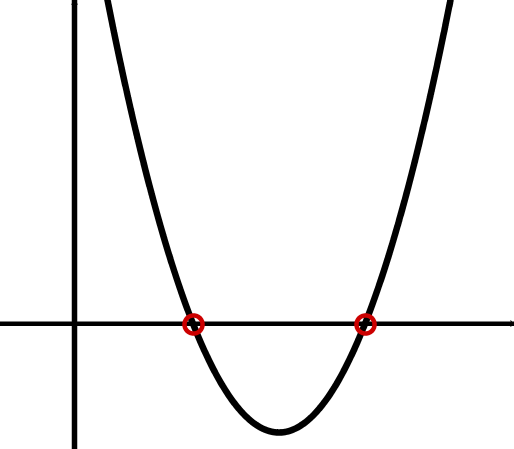
To determine the location of the zeros, one must solve a quadratic equation, e.g. using the quadratic solution formula, where the function must be set equal to $0$ .

Vertex

The vertex of a parabola is always at its extremum. It always lies at $x = - \frac{b}{2 a}$ .

The vertex of a parabola is obtained either by completing the square or, as with all functions, by the first derivative.

If you insert the $x$ -value into the equation of the quadratic function, you get the vertex, which then has the coordinates:

S = (- \frac{b}{2 \cdot a} | c - \frac{b^{2}}{4 \cdot a})

Forms of a quadratic function

The function term of a quadratic function can be - perhaps after a transformation - in one of the following forms:

General form: $𝒇 (𝐱) = 𝒂 𝒙^{𝟐} + 𝒃 𝒙 + 𝒄 f (x) = a x 2 + b x + c$

Vertex form: $𝒇 (𝐱) = 𝒂 (𝒙 - 𝒅)^{𝟐} + 𝒆$

Zero form / Linear factor form $𝒇 (𝒙) = 𝒂 (𝒙 - 𝒙_{𝟏}) (𝒙 - 𝒙_{𝟐})$ (only if $f$ has zeros)

Meaning of the coefficients of a quadratic function

A quadratic function in general form has an equation of the form $f (x) = a x^{2} + b x + c$ .

The coefficients $a$ , $b$ and $c$ deform and / or shift the parabola. However, the exact influence they have on the shape of the graph can be directly seen in the vertex form.

Compare the article Influence of parameters in the vertex form.

This content is licensed under
CC BY-SA 4.0 → What does that mean? serlo.org