Repeating Decimals

A repeating decimal is a decimal number with an infinite sequence of digits, in which a certain finite block of digits is repeated infinitely often.

To denote a repeating decimal, you put a horizontal line above the digits, which are to be repeated.

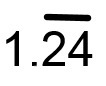
Example	Sprechweise
The fraction $\frac{1}{3}=0.333333333\ldots=0.\overline{3}$ has the repeating block 3.	You may read this number as: Zero point repeating three.
The fraction $\frac{16}{99}=0.161616161616\ldots=0.\overline{16}$ has the repeating block 16.	You may read this number as: Zero point repeating one six.
The fraction $\frac{1}{6}=0.1666666\ldots=0.1\overline{6}$ has the repeating block 6 (not 16)	You may read this number as: Zero point one repeating six.
The fraction $\frac{2}{7}=0.\overline{285714}$ has the repeating block 285714.	You may read this number as: Zero point repeating two eight five seven one four.
The fraction $\frac{3}{4}=0.75$ has no repeating decimals.	You may read this number as: Zero point seven five.

AttentionDifferent notations

Depending on where you live, people may also use other notations for repeating decimals. Instead of writing $1.24242424 \ldots = 1.\overline{24}$ , it may also be common to write

$1.24242424 \ldots = 1.\dot{2} \dot{4}$
$1.24242424 \ldots = 1.(24)$
$1.24242424\ldots=1.\overset{\frown}{24}$

Instead of one point repeating two four, this number may also be pronounced as

One point repeated two four
One point recurring two four
One point repetend two four
One point into infinity two four

Pure periodic decimal numbers

Pure periodic decimal numbers are repeating decimals in which the repetition of decimals begins directly after the decimal point.

Example

$0.\overline{78}$
$1.\overline{7}$
$8.\overline{478}$

Mixed periodic decimal numbers

Mixed periodic decimal numbers are repeating decimals with one or more numbers between the decimal point and the repeated block, i.e. the repeated block does not start directly after the decimal point.

Example

$2.5\overline{35}$
$524.57\overline{924}$
$35.6\overline{534}$

Converting a periodic decimal number into a fraction

A periodic decimal number can always be written as a fraction. You can read how this works in the article about converting decimal numbers into fractions.

Theorem about the length of a repeating block

TheoremTheorem about the length of a repeating block

Each decimal number can have a repeating block at most as long as the denominator in the corresponding fraction, minus 1.

Example

The fraction $\frac17$ has a repeating block of length no larger than 6, since $7-1=6$ . Indeed,

$\frac{1}{7}=0.\overline{142857}$ has a repeating block of length 6.

The fraction $\frac1{17}$ has a repeating block of length no larger than 16, since $17-1=16$ . Indeed,

$\frac{1}{17}=0.\overline{0588235294117647}$ has a repeating block of length 16 (quite impressive!).

The fraction $\frac13$ has a repeating block of length no larger than 2, since $3-1=2$ . Indeed,

$\frac{1}{3}=0.\overline{3}$ has a repeating block of length 1 (even shorter than 2).

The last example clearly shows that the theorem only makes a statement about the maximum period length (and not about the exact period length). The exact length can be shorter.

Fun fact for nerds: The theorem is valid in all positional systems. For instance, $0.{\overline{5\mathrm B}}_{17}$ would be the hepta-decimal system's equivalent of our $\frac13$ .

Uniqueness of the decimal representation

Attention

Repeating decimals are sometimes equal to other numbers, which are not repeating decimals. For instance,

$0.\overline{9}=1$

Yes, both numbers are really equal! $0.\overline{9}$ is just a different way of writing $1$ . So with repeating decimals, we sometimes get more than one option to write the same lnumber.

Many other numbers also have more than one representation as a decimal number:

$2=1.\overline9$
$0.25=0.24\overline9$
and so on...

Infinite, non-periodic decimals

There are also decimal numbers that have an infinite number of decimal places, where no repeating blocks occur. Such numbers are called irrational numbers and they are a subset of the so-called real numbers.

One of the most prominent numbers with infinitely many non-repeating decimal places is $\pi$ :

$\pi =3.14159265358979323…$

Attention

Irrational numbers cannot be represented as a fraction of two integers!

This content is licensed under
CC BY-SA 4.0 → Info