Asymptote
An asymptote is a curve (often even a line) to which the graph of a function increasingly approaches.
"Approaching" here means that the distance between the asymptote and the graph of the function becomes arbitrarily small if you are
far enough away from the origin:
along the x-axis, or
along the y-axis.
Attention! It can also happen that this distance becomes zero at some point (i.e. that the function is equal to its asymptote).
One often speaks of the behaviour at infinity of the function when considering it far away from the origin along the x-axis.
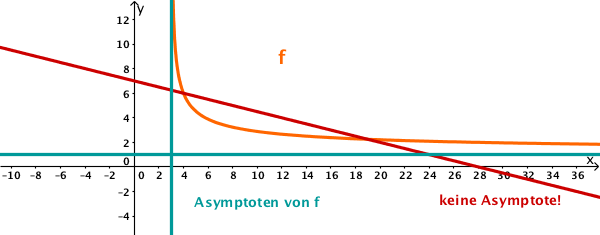
Sind Funktionsgraph und Asymptote immer nah aneinander?
Es kann passieren, dass der Funktionsgraph und die Asymptote in einem Abschnitt auseinandergehen. Genau so können sie sich manchmal berühren oder sogar schneiden.
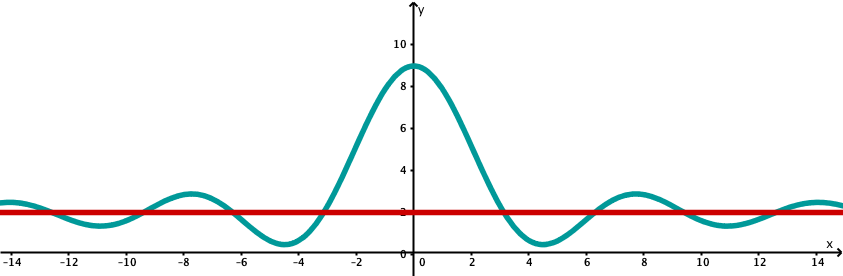
Das folgende Beispiel veranschaulicht eine Funktion, die ihre Asymptote unendlich oft schneidet!
Hier sieht man nur, dass die Funktion um die Gerade bei schwingt.
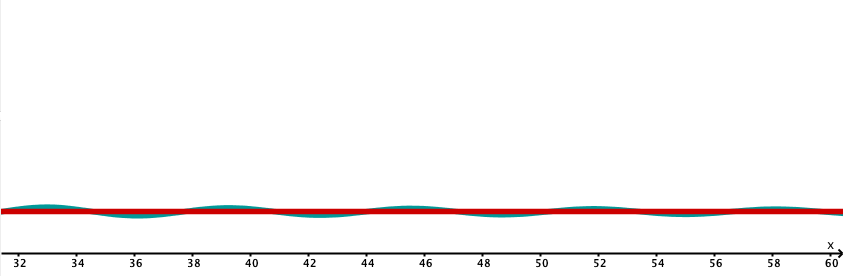
Wenn man in positive Richtung entlang der x-Achse geht wird deutlich, dass die Asymptote der Funktion ist.
Unterscheidung von Asymptoten
Man unterscheidet zwischen vier Arten von Asymptoten:
Waagrechte Asymptote
Diese sind Geraden, die parallel zur x-Achse verlaufen. Diese sind genau die konstanten Funktionen.
Eine Funktion kann höchstens zwei waagrechte Asymptoten haben, nämlich wenn
ganz groß wird (also wenn gegen geht) oder,
wenn ganz klein wird (also gegen geht)
Waagerechte Asymptote bei :
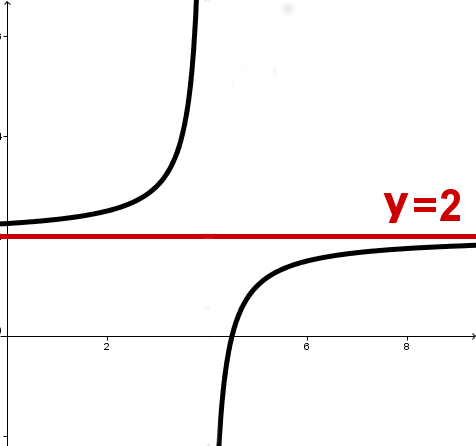
Senkrechte Asymptote (Unendlichkeitsstelle):
Diese sind Geraden, die parallel zur y-Achse verlaufen und werden auch als Polstellen bezeichnet.
Die Funktion aus dem obigen Beispiel hat auch eine senkrechte Asymptote.
Senkrechte Asymptote bei .

Schiefe Asymptote
Bei einer schiefen Asymptote sind weder - noch -Wert konstant.
Die Asymptote wird durch eine allgemeinere Geradengleichung angegeben.
Schiefe Asymptote mit Geradengleichung .
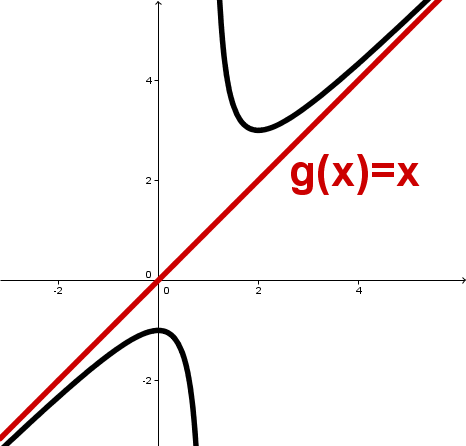
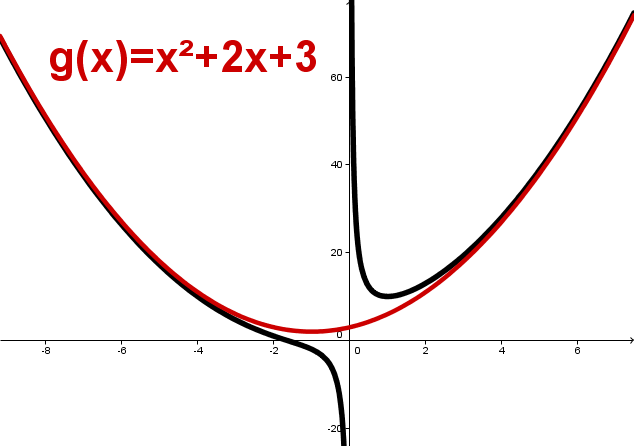
Kurvenförmige Asymptote
Der Graph einer Funktion kann sich einem anderen Funktionsgraphen als einer Geraden annähern.
Bei gebrochenrationalen Funktionen lässt sich ihre Asymptote gut berechnen.
Exercises
You can find more exercises in the following folder::
Aufgaben zum Berechnen von Asymptoten
Still want more?
You can find more content on this topic here: