Shifts and stretchings of hyperbolas

Abbilden der Standardhyperbel

Der Graph der Funktion $f$ entsteht aus dem Graphen der Funktion von $g(x)=\frac{1}{x}$ (Standardhyperbel) durch:

• Verschiebung nach unten oder $\text{oben}$ (Veränderung von $\text{c}$)

• Verschiebung nach links oder $\text{rechts}$ (Veränderung von $𝐛$),

• $\text{Spiegelung}$, $\text{Stauchung}$ und Streckung (Veränderung von $𝐚$)

Der Reihe nach kannst du hier die Veränderungen der Funktion $g\left(x\right)=\frac{1}{x}$ durch die Parameter $a$, $b$ oder $c$ nachvollziehen.

Verschiebung nach unten und oben

Der Parameter $c$ der Funktion $f(x)=\frac{a}{x+b}+c$ verschiebt den Graphen der Funktion $g(x)=\frac{1}{x}$ nach unten bzw. oben.

• $c>0\Rightarrow$ Verschiebung um $\left|c\right|$ nach oben

• $c<0\Rightarrow$ Verschiebung um $|c|$ nach unten

Beispiel für eine Verschiebung nach unten

Vergleiche anhand einer Tabelle die Funktionswerte von $f_1(x)=\frac{1}{x}$ und $f_2(x)=\frac{1}{x}-4.$ (An der Stelle x=0 sind die beiden Funktionen nicht definiert: nd. = nicht definiert)

Im Koordinatenystem kannst du nun $f_1$ und $f_2$ skizzieren.

Durch Vergleich der Graphen von $f_1$ und $f_2$ kannst du erkennen, dass der Graph von $f_2$ aus dem Graphen von $f_1$ entsteht. Wenn du den Graphen von $f_1$ um $4$ nach unten verschiebst, erhältst du den Graphen von $f_2$.

Veränderung der Asymptoten

• Die senkrechte Asymptote der Hyperbel verändert sich durch eine Verschiebung um $\left|c\right|$ nach unten bzw. oben nicht.

• Die waagrechte Asymptote der Hyperbel verschiebt sich (wie der Graph selbst) um $\left|c\right|$ nach oben bzw. unten.

Verschiebungen nach links und rechts

Der Parameter $b$ der Funktion $f(x)=\frac{a}{x+b}+c$ verschiebt den Graphen der Funktion $g(x)=\frac{1}{x}$ nach links bzw. rechts.

• $b>0\Rightarrow$ Verschiebung um $\left|b\right|$ nach links

• $b<0\Rightarrow$ Verschiebung um $\left|b\right|$ nach rechts

Beispiel für eine Verschiebung nach rechts

Vergleiche anhand einer Tabelle die Funktionswerte von $f_1(x)=\frac{1}{x}$ und $f_2(x)=\frac{1}{x-2}.$

(An den Stellen $x=0$ bzw. $x=2$ sind die beiden Funktionen nicht definiert: nd. = nicht definiert)

Die Zeilen der Tabelle von $f_1\left(x\right)$ und $f_2\left(x\right)$ sehen sich sehr ähnlich. Sie enthalten die gleichen Werte, nur an anderer Stelle $x$. Die Funktionswerte sind in der Tabelle um 2 nach rechts verschoben.

Im Koodinatensystem sehen die Hyperbeln dann so aus:

Durch Vergleich der Graphen von $f_1$ und $f_2$ kannst du erkennen, dass der Graph von $f_2$ aus dem Graphen von $f_1$ entsteht. Wenn du den Graphen von $f_1$ um $2$ nach rechts verschiebst, erhältst du den Graphen von $f_2$.

Veränderung der Asymptoten

• Die waagrechte Asymptote der Hyperbel verschiebt sich durch Änderung des Parameters $b$ nicht.

• Die senkrechte Asymptote der Hyperbel verschiebt sich (wie der Graph selbst) um $\left|b\right|$ nach rechts bzw. links.

Stauchen und Strecken der Hyperbel

Der Parameter $a$ der Funktion $f(x)=\frac{a}{x+b}+c$ staucht bzw. streckt den Graphen der Funktion $g(x)=\frac{1}{x}$. Hier betrachten wir erstmal nur positive Werte für $a$, also $a>0$.

• $a\in ]0;1]\Rightarrow$ Stauchung

• $a>1\Rightarrow$ Streckung

Beispiel für eine Streckung

Vergleiche anhand einer Tabelle die Funktionswerte von $f_1(x)=\frac{1}{x}$ und $f_2(x)=\frac{4}{x}$.

(An der Stelle $x=0$ sind die beiden Funktionen nicht definiert: nd. = nicht definiert)

Die Funktionswerte $f_1(x)$ werden mit dem Faktor $4$ multipliziert. So erhältst du die Werte $f_2(x)$.

Im Koordinatensystem sehen die Hyperbeln dann so aus:

Die y-Werte der Punkte auf der Hyperbel von $f_1$ werden mit dem Faktor $4$ multipliziert und die Hyperbel so nach außen gestreckt. Die gestreckte Hyperbel ist dann der Graph von $f_2$.

Veränderung der Asymptoten

Die Asymptoten ändern sich durch Stauchung und Streckung des Graphen nicht.

Spiegeln der Hyperbel

Der Parameter $a$ der Funktion $f(x)=\frac{a}{x+b}+c$ spiegelt den Graphen der Funktion $g(x)=\frac{1}{x}$ für negative Werte von $a$ an der waagrechten Asymptoten von $f$.

Beispiel

Vergleiche anhand einer Tabelle die Funktionswerte von $f_1(x)=\frac{1}{x}$ und $f_2(x)=\frac{-1}{x}=-\frac{1}{x}$.

(An der Stelle $x=0$ sind die beiden Funktionen nicht definiert: nd. = nicht definiert)

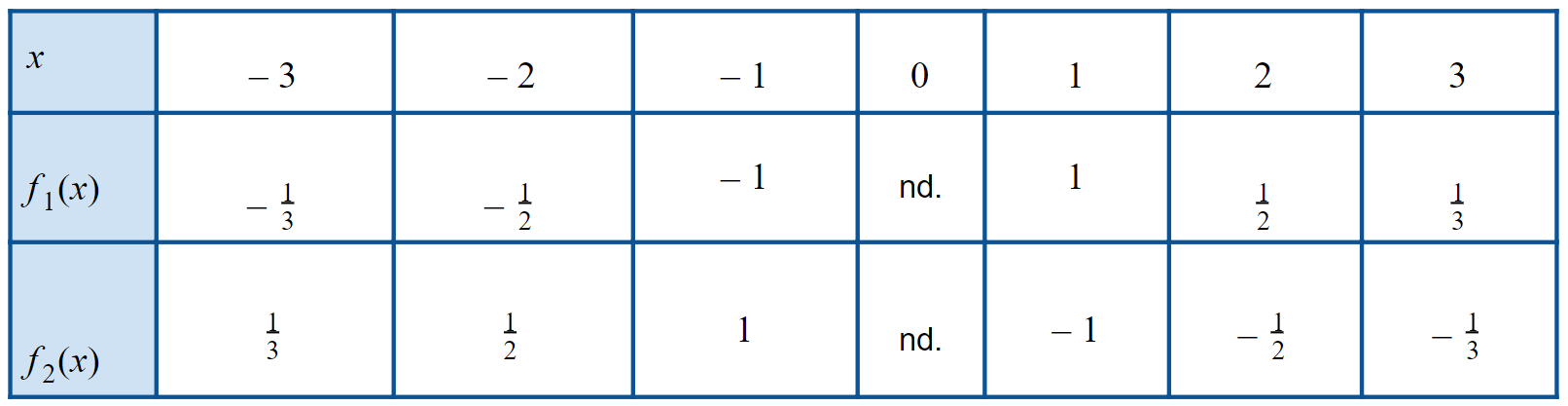
Wechselt man das Vorzeichen von $f_1(x)$, erhält man die Werte von $f_2(x)$.

Die Hyperben sehen im Koordinatensystem dann so aus:

Der Graph von $f_1$ wurde an der waagrechten Asymptote von $f_1$ (und zwar $x=0$) gespiegelt. So erhält man den Graphen von $f_2$.

Veränderung der Asymptoten

Die Asymptoten ändern sich durch eine Spiegelung nicht.

Verknüpfung der verschiedenen Parameter

Die Verschiebungen nach oben/unten und links/rechts sowie die Stauchung/Streckung und Spiegelung kannst du auch miteinander verbinden.

Im folgenden Applet kannst du dir für verschiedene Werte von $a$, $b$ und $c$ den Graphen der Funktion $f(x)=\frac{a}{x+b}+c$ zeichnen lassen. Bewege hierfür den roten, lila und türkisen Schieberegler.

Durch Klicken auf die Kästchen "waagrechte Asymptote" und "senkrechte Asymptote" kannst du dir die entsprechenden Asymptoten des Graphen ein- und ausblenden.

Aufgaben

Übungsaufgaben zu diesem Thema findest du im Aufgabenordner Aufgaben zu einfachen gebrochen-rationale Funktionen.