Rounding Decimal Numbers

Step 2

Separate the number into two parts:

• The first part includes everything up to and including the digit to which the number should be rounded.

• Everything afterwards constitutes the second part.

Example:

To round $41.6581724$ to the nearest hundredth, you need to split the number after the second decimal place: $41.65\, |\,81724$

Step 3

Look at the first digit of the second part of the number (the decimal place immediately after the one to which the number should be rounded.

• If this digit is a $0{,}1,2{,}3$ or $4$ you need to round down - the rounded number is the same as the first part of the original one.

Example:

Rounding $5.824178$ to the nearest thousandth yields the number $5.824$ because the digit after the third decimal place is a $1$.

• If this digit is a $5{,}6,7{,}8$ or $9$ you need to round up by increasing the last digit of the first part of the number by $1$. (If the last digit was a $9$ before rounding, you need to adjust the other decimal places accordingly)

Examples

• Rounding $41.69$ to the nearest tenth yields $41.7$.

• Rounding $8.2419278$ to the fourth decimal place yields $8.2420$.

• Rounding $279.9999$ to the nearest thousandth yields $280.000$ - in this example, multiple decimal places need to be adjusted.

• Rounding $9.99742$ to the nearest hundredth yields $10.00$.

Rounding to integers

Rounding to integers means finding the integer that is closest to the given decimal number. If the decimal number is an integer, then the closest integer is the integer itself.

• You round down if the digit before the decimal point (tenth) is between 0, 1, 2, 3 or 4.

• You round down if the digit before the decimal point (tenth) is between 5, 6, 7, 8 or 9.

Examples in the place value chart

• 0.77 is rounded to 1 because the tenth digit is a 7.

• 1.26 is rounded down to 1 because the tenth digit is a 2.

• 1.5 is rounded up to 2 because the tenth digit is a 5.

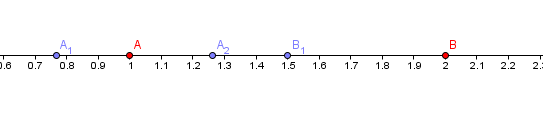
Examples on the number line

$\text{A}_1=0.77$ and $\text{A}_2=1.26$ are rounded to $\text{A}=1$ , $\text{B}_1=1.5$ is rounded to $\text{B}=2$.

Calculation examples

$2.3\approx2$

Because the tenths digit 3 lies between 0 and 4, it is rounded down,

i.e. the 2 is left standing.

$3.7\approx4$

Because the tenths digit 7 lies between 5 and 9, it is rounded up,

i.e. the 3 becomes the 4.

$2.48\approx2$

Because the tenths digit 4 lies between 0 and 4, it is rounded down,

i.e. the 2 is left standing.

Reasonable rounding

Frequently, you need to round without anyone telling you, to which digit. Often, this happens when calculating with units of measurement or currencies. So what is a reasonable choice for the digit you round to?

For currencies, it is common to round to integers (₹) or hundredths ($\$, \pounds, €$ ), depending on what is the smallest amount that you can pay with coins.

For units of measurement, there are often several reasonable rounding options, depending on the situation. Typically, 2-3 digits in total are OK. If you need high-precision results, also 4 or even 5 diigits may be required. Sometimes, also 1 digit is OK for a rough estimate.

Sample task:

Peter drives 20 minutes by car. He consistently drives 100 km/h. How far did Peter drive? Round the result reasonably.

Solution:

20 minutes are $\dfrac{1}{3}$ hour. In one hour it covers 100 kilometers, so in $\dfrac{1}{3}$ hour $\frac{1}{3}\cdot100 = 33.\overline3$ kilometers. So there are infinitely many digits, down to meters, millimeters, nanometers, and so on. For long distances covered by car, it is not useful to specify the distance in millimeters or even more precise! Typically, it is OK to round to full kilometers, since this is how distances are indicated on road signs.

$\Rightarrow$ Peter has driven $\approx 33$ kilometers.

But depending on the situation, it would also be OK, to round to $33.3$ or $33.33$ or $33.333$ kilometers (if you really want to be precise) or to $30$ kilometers (as a rough estimate).