Position, displacement, and distance

Everything is moving. Even if you stop and don’t even move a finger, you are still moving relative to the Sun. An object’s motion can be described by tracking its position in time. So, to be able to define an object’s movement, first we need to understand its position.

Position

DefinitionPosition

Position is a measurement of a location according to a reference point. The symbol “x” is used for denotation and it has units of lengths (ie. mm, cm, m, km etc.).

Below, you see the position of a house. You can define it as 500 m from the school (if you take the reference point as school) or 1000 m from the park (if the park is the reference point). The position of the library is also from 1000 from the park. However, it is in the opposite direction to the house.

Let’s take the park as a reference point. This means that the position of the park will be 0 m. Then the direction to the library will be positive, and to home will be negative.

In this case, the position of the house will be - 1000 m and the position of the library will be + 1000 m.

In short we can write it as following:

\displaystyle \def\arraystretch{1.25} \begin{aligned} x_{park} &= 0\ m\\ x_{house} &= -1000\ m \\ x_{library} &= +1000\ m\\ x_{market} &= +500\ m\\ x_{school} &= -500\ m \end{aligned}

Displacement and Distance

DefinitionDisplacement

Displacement is defined as the change in position. This means that displacement depends only on the initial ( $x_{i}$ ) and the final position ( $x_{f}$ ) of an object.

We can find it as following:

\displaystyle Δx=x_f-x_i

Beachte

Δ (delta) is a Greek alphabet letter to indicate a change in a quantity. To denote displacement (which is the change in position) we use Δx. In the case of change in time (t) we use Δt.

Let’s turn back to our example. Consider yourself going out from the market to the library.

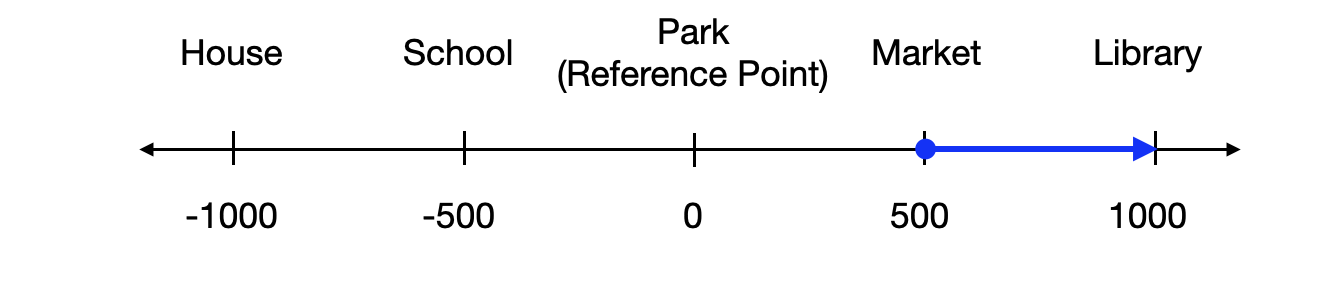
Your displacement would be 500 m. In other words:

\displaystyle \def\arraystretch{1.25} \begin{aligned} Δx &=x_f-x_i \\ Δx &=1000 - 500 \\ Δx &=500\ m. \end{aligned}

What would be your displacement if you would turn back to the market?

The answer is zero. There would be no change in your position.

\displaystyle \def\arraystretch{1.25} \begin{aligned} Δx &=x_f-x_i \\ Δx &=500 - 500 \\ Δx &=0\ m. \end{aligned}

So if you leave your house to spend the time outside to visit the library, the market, and the park, when you return to your house, your displacement would be zero. That is because there was no change in your position. However, you may say that you visited so many places and walked a lot. This is the distance that you traveled and it is different from displacement.

DefinitionDistance traveled

Distance traveled means the total length of the path traveled between two positions.

Let’s calculate the displacement and the distance traveled for the following example: Suppose that you followed the path first from "D to G" and then "G to C". What would be the displacement and distance you traveled?

\displaystyle \def\arraystretch{1.25} \begin{aligned} Displacement(Δx) &= x_f - xi \\ Δx &= -200-(-100) \\ Δx &= -100 m. \end{aligned}

\displaystyle \def\arraystretch{1.25} \begin{aligned} Distance (d) &= path\ traveled \\ d &=300 + 400 \\ d &=700\ m. \end{aligned}

Beachte

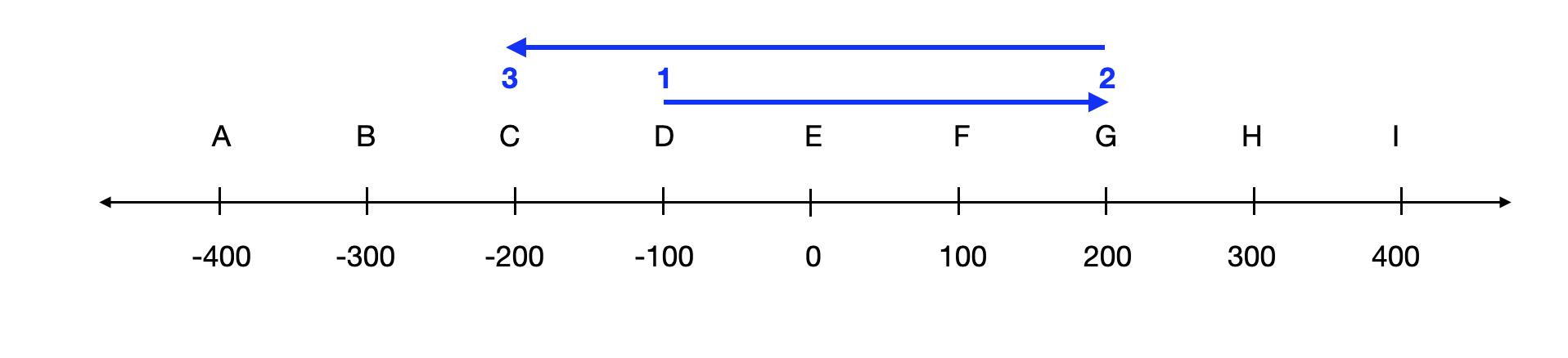
Displacement also indicates the direction of the motion which means it can be positive or negative. On the other hand, distance traveled can only be positive.

This content is licensed under
CC BY-SA 4.0 → Info