Introduction: Systems of Linear Equations - Part 2
1 Overview
Content
In this course you will learn what a solution set is, how many solutions there can be to a linear equation system, and what other solution methods there are besides the elimination by equating coefficients.
Prerequisites
You should already know what an intersection point is and how to determine it both graphically and computationally. Also, for this course you need to know what a linear system is.
If you don't know any of this yet, check out the first part of the introductory course on systems of linear equations before.
Duration
This course takes about 2 hours.
2 The birthday party of Tina's parents
Tina's parents are celebrating their birthday together this year.
Tina has a guilty conscience, because she has forgotten how old they are!

Her father makes a riddle out of it:
"If you double my age and add half your mother's age to her age, that adds up to 150 years."
That didn't help Tina much.
Her mother says:
"If you add three years to my age and subtract two years from your father's, we're the same age!"
Tina is currently going through systems of equations at school and now wants to try to use them to figure out her parents' ages.
She runs and gets a pencil and pad.
Now she can calculate how old her parents are.
Try it for yourself!
3 Recap: Linear systems and elimination by equating
To find out the age of Tina's parents, it is useful for you to recall the linear system and the elimination by equating coefficients.
What is a linear system?
A linear system of equations has often had two equations of the form , with variables and .
You got to know the solution of alinear system as the intersection point of these lines.
Solution via elimination by equating coefficients
The away how elimination by equating coefficients works is already hidden in its name. The keyword is equating. For this you have to proceed as follows:
Solve each of the equations of the system of equations for the same variable.
Set the equations equal.
Solve the resulting equation for the remaining unknown.
Plug this variable into one of the original equations.
4 The age of the parents as equations
Tina's parents gave her good hints to make two equations.
Father: "If you double my age and add half of your mother's age to her age, that adds up to 150 years."
First, Tina defines some variables.
age of the mother
age of the father
From the father's statement, Tina gets the first equation:
Double the father's age:
Add half to the mother's age:
Mother: "If you add three years to my age and subtract two years from your father's, we are the same age!"
Add to the mother's age:
Subtract from the father's age:
5 Solution set
The two equations of Tina's parents do not have much to do with straight lines!
Even if you can transform them in such a way that one can draw them, this is not very descriptive in the subject context.
That's why in many tasks you don't give the solution as an intersection point, but as a solution set:
For example, if you have a system that is solved for the values and , you write:
If you sort the variables alphabetically, you can also use the last and shorter notation.
6 How many solutions exist? (1/2)
When you solve a linear system of equations, cases can occur:
When calculating the solution you find a wrong statement (e.g. = ).
You find out during the transformation that the equations are identical. The result is a statement that is true no matter which number you insert (e.g. ).
When calculating the solution you get a unique variable assignment for the equations of the system (e.g. and ). This is the already known usualcase!
Panic. What to do in case 1. or 2.?
Don't worry! Even linear systems of equations cannot always be perfect. :-)
There are types of systems: Those with , or solutions.
7 How many solutions exist? (2/2)
How do you find out what solution type you have?
The three different solution types are explained with examples.
Case 1: No solution
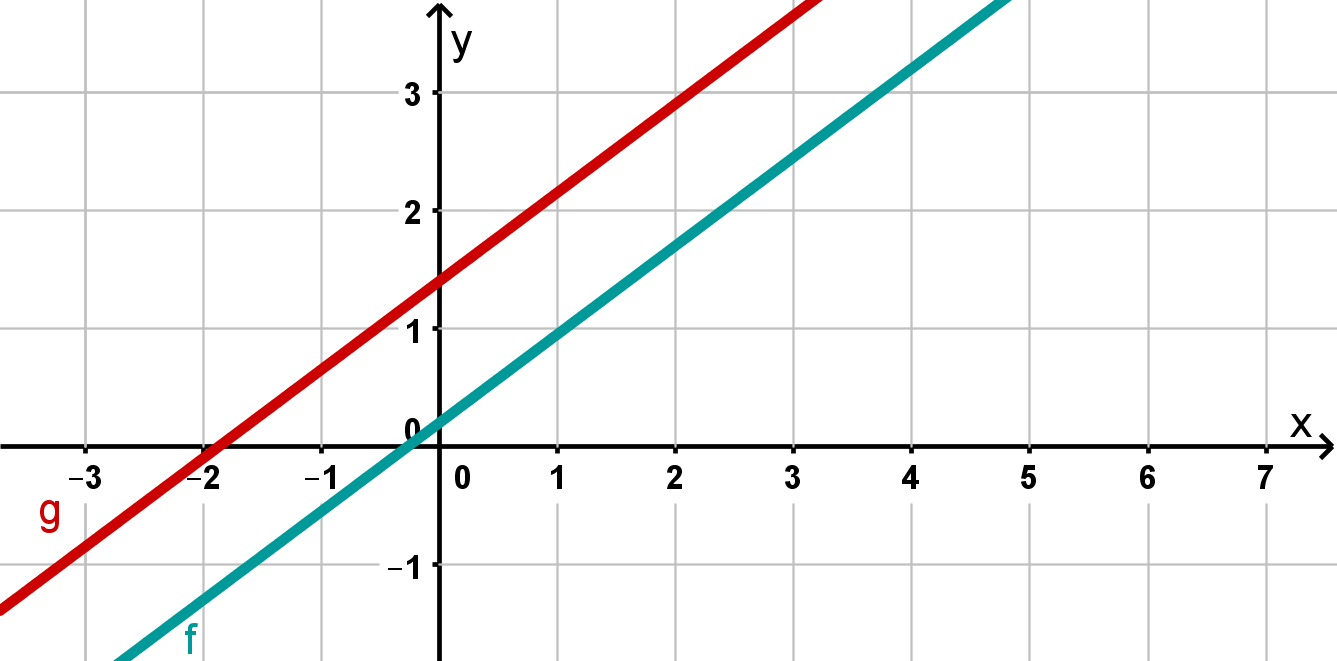
In the graphic you can see two parallel lines. You can see this because they have the same slope , but different -axis intercepts. The straight lines never intersect, so there is no solution.
In this case, the solution set is the empty set:
or .
Case 2: one solution
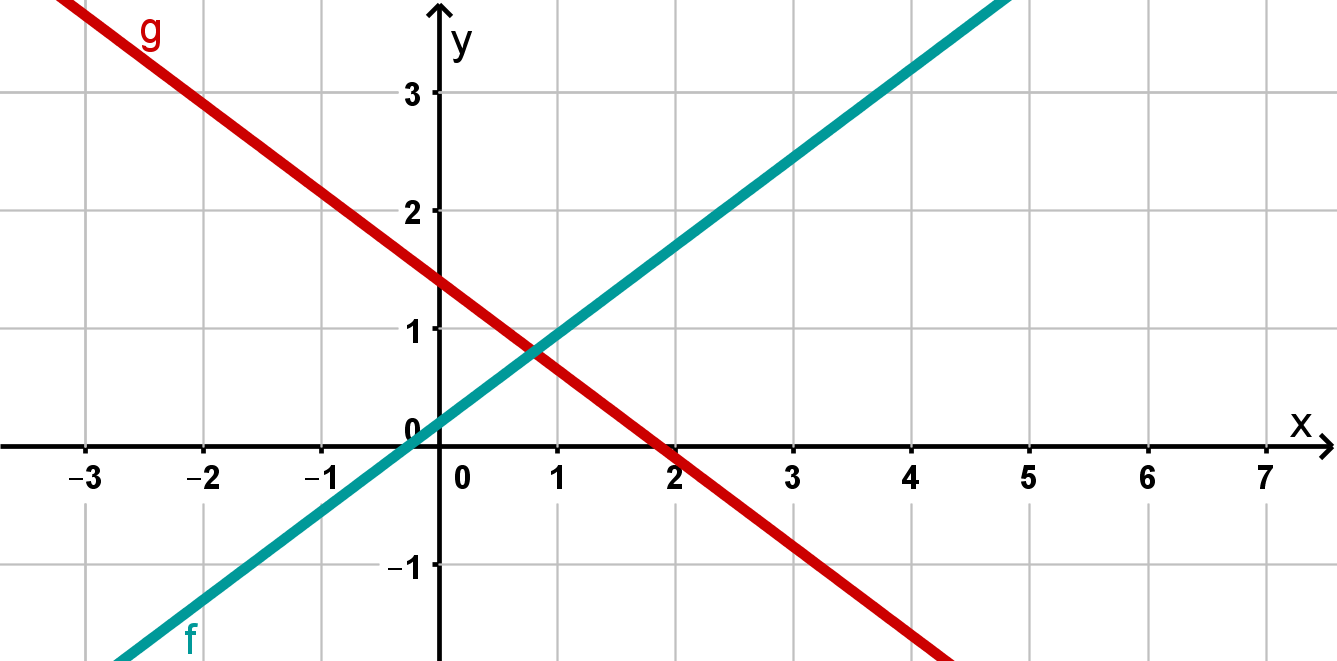
You can see from the graphic that the lines cross at an intersection point. This is always the case when both lines have different slopes. So there is exactly one solution.
The solution set here is simply again your number pair .
Case 3: Infinitely many solutions
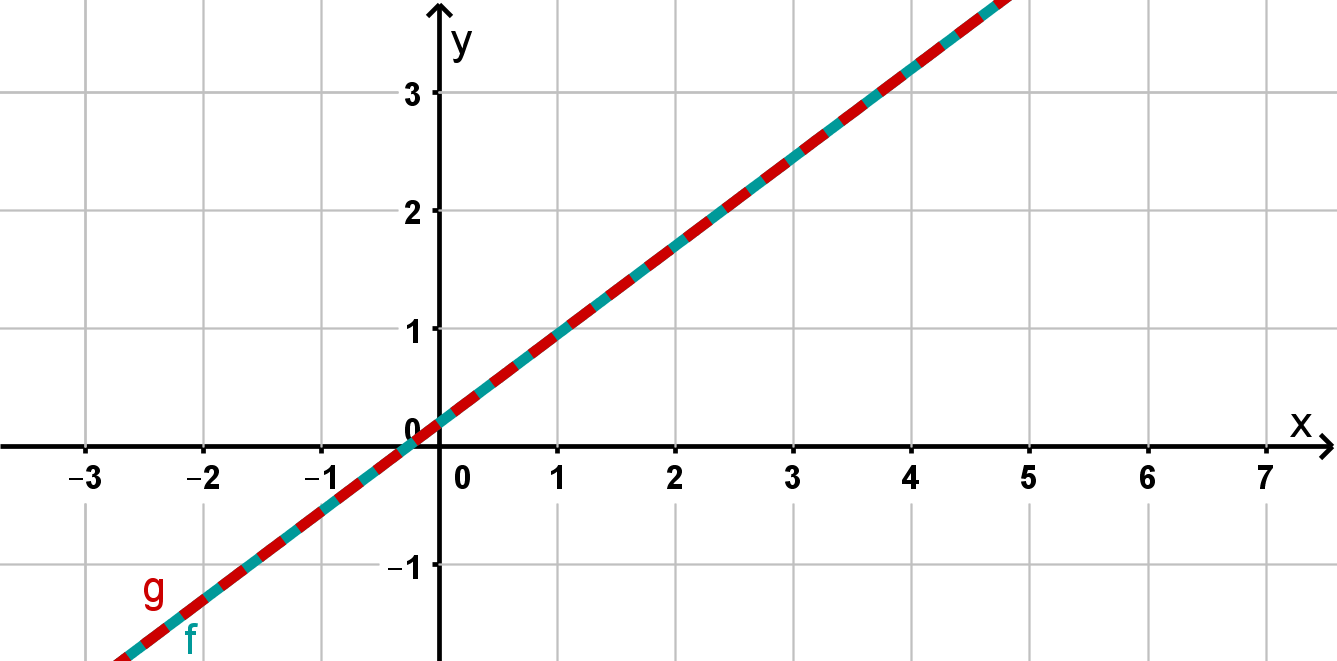
If you transform both equations, you will see that both lines have the same slope and the same -axis intercept. They are therefore identical.
Every point on the lines is an intersection point. So there are infinitely many solutions.
The solution set here is the special case, namely: , that is, all pairs of numbers with the property that they satisfy the equation .
8 Substitution method
In the first part of the introductory course you have already learned how to set up a system of linear equations (LGS) and solve it with the equation method.
However, there are also other methods to solve a LGS!
The substitution method is very similar to the elimination by equation.
Why do we use it?
Quite simply, it is less work than the equation method!
How does it work?
The substitution method works like this:
Solve only one of the two equations by one of the two variables.
Substitute the variable you solved for into the other of the two equations.
You get a value, which you again insert into one of the equations. This already gives you the solution.
Sounds complicated? Actually, it is not! This is how it looks:
9 Example: substitution method
Now look at the equations that give the ages of Tina's father and mother.
Solve the problem using the substitution method:
Step 1: Resolve equation
Which equation you solve for which unknown is partly a "sharp look", partly a matter of taste! Here the equation is solved for .
Step 2: Plug into
Step 3: Plug m into
Tina now knows how old her parents are thanks to you. Her mother is years old and her father is years old.
You can also write this down formally as a solution set:
.
10 Exercises: substitution method
Loading
Loading
11 Adding/Subtracting equations
You can add one equation to another. This gives you a new equation.
Why does this work?
Visually, you can imagine each equation as a scale. Each of its scales represents one side of the equation.
The equations of the scales are:
Scale 1:
Scale 2:
Then, put the contents of each of the left-hand sides and the contents of the right-hand sides together on a third scale. The balance remains in equilibrium!
Mathematically, it looks like this:
Scale 3:
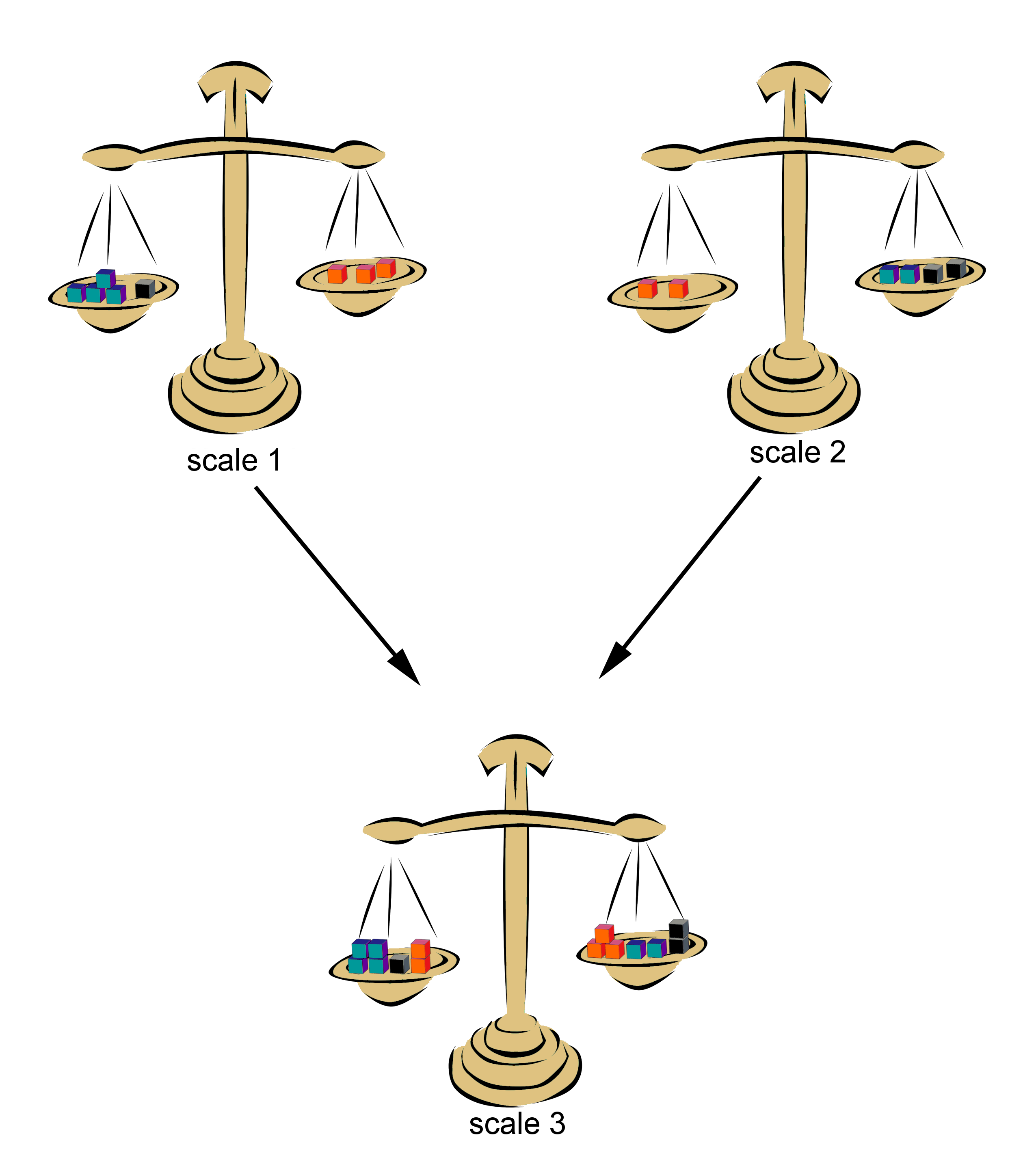
The same way, you can subtract two equations from each other.
What happens when adding/subtracting equations?
When you add/subtract equations, you add/subtract two equations that become a new equation.
How is equality sustained?
Don't be confused by the fact that you have to add/subtract two equations instead of numbers as usual! To do this, consider the left and right sides of each equation as one coherent part.
You proceed as follows:
Add/subtract the respective left sides of the two equations and then conclude.
Add/subtract the respective right sides of the two equations and then conclude.
Put a between the new left and right sides, to obtain your new equation.
It is useful to "prepare" the equations before adding/subtracting them.
This means, for example, to put all variables (with their coefficients) on the left sides of the equations and all numbers without variables on the right sides.
In no time at all, you have easily added/subtracted two equations to create a new equation!
On the next page you will see how you can apply this new knowledge to solve linear systems.
12 Addition method (1/2)
The third method for solving LGS is the addition method.
The goal of this method is to remove a variable by cleverly adding/subtracting the equations of the linear system.
Step 0: Tidying up the equations and selecting variables
First, for your equations, bring all the unknowns (with their coefficients) to the same side.
Look at the equations and with a sharp eye.
For example, is one of the variables in the first equation an integer multiple of itself in the second equation?
Then select that variable.
In the following example, in the is on both sides and in both variablesare not together on one side.
Clean up.
Here both variables are suitable! In step 1, you see why.
Step 1: Multiplying the equations
In each case you have to multiply/divide the equations and/or such that the coefficients of the selected variables are equal (best according to the least common multiple).
Here you do not have to pay attention to the sign, but only to the coefficient.
13 Addition method (2/2)
Step 2: Removal of a variable by addition/subtraction.
Case 1: Addition of equations
The selected variable is contained once with positive sign and once with negative sign in the equations and .
Now add the two equations and as above.
Case 2: Subtraction of the equations
The selected variable is contained twice with the same sign in the equations and .
Now subtract the two equations and as above.
Step 3: Determine the values of the two variables
The new equation contains only one variable.
Solve it and find out its value.
By inserting this value into one of the equations or , you determine the numerical value of the other variable.
14 Example: Addition method
The birthday example is now also solved using the addition method.
You have already seen the linear system of equations for this problem in this course:
Step 0: Clean up the equation and select a variable
Now the equations are tidy and you have to select one of the variables. It is important to select the variable so that the next steps are as easy as possible. Remember: It's all a matter of practice!
Multiplying is usually easier than dividing, that's why the variable v was chosen here.
In the equation you have:
In the equation you have:
So you have to calculate .
1st step: multiply the equation
15 Example: Addition method
Step 2: Removing one variable
Now both equations have both the unknowns and the numbers below each other.
The signs of are different, so you add the equations.
Now there is only one variable left!
Step 3: Determine the values of the two variables
First solve the equation from step 2
Substitute into one of the two equations
For example, substituted into :
So again, the mother is 40 years old and the father is 45 years old!
.
16 Exercises: Addition method
Loading
Loading
17 When to use which method?
Elimination by equating coefficients
The elimination by equating coefficients is useful if both equations are already solved for the same variable or you can easily solve both equations for the same variable.
Substitution method
The substitution method is useful if one equation is already solved for one variable or can easily be solved for one variable. You can thus easily substitute it into the other equation.
Addition method
You should use the addition/subtraction method if both equations have the same variable with the same coefficient (e.g. in both equations). Based on the sign you decide whether you have to add or subtract.
18 Recap
Solution set
Number of solutions
A linear system of equations can have none, one or infinitely many solutions
Elimination by equating coefficients
Step 0: Solve both equations for one variable.
Step 1: Equate the other two sides.
Step 2: Solve for the remaining variable.
Step 3: Insert the obtained value into one of the equations.
Substitution method
Step 1: Solve an equation for one variable.
Step 2: Substitute into the other equation.
Step 3: Substitute the obtained value into one of the equations.
Addition method
Step 0: Clean up the equation and select one variable.
Step 1: Multiply the equations.
Step 2: Remove of the variables.
Step 3: Determine the values.
19 Show what you have learned!
Loading
Loading
Loading
Loading
Loading