Sine and Cosine theorem on a triangle

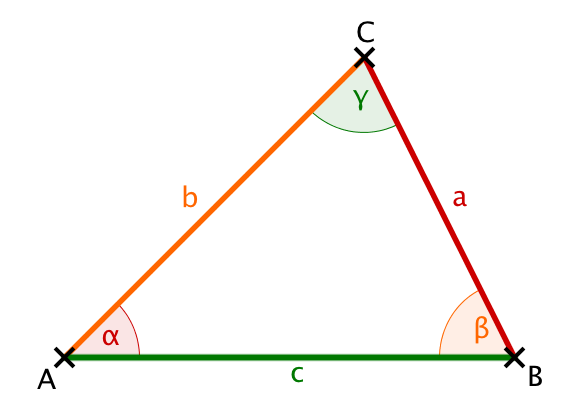
Alternative formulation of the sine theorem

By transformations, the sine theorem can also be brought to the following forms:

$\frac{a}{b}=\frac{\sin \left(\alpha \right)}{\sin \left(\beta \right)}$ $\frac{a}{c}=\frac{\sin \left(\alpha \right)}{\sin \left(\gamma \right)}$ $\frac{b}{c}=\frac{\sin \left(\beta \right)}{\sin \left(\gamma \right)}$

The Pythagorean theorem as a special case of the cosine theorem

For $\gamma ={90}^{\circ }$ we obtain a right triangle with $\cos ({90}^{\circ })=0$. So the Phthagorean theorem $c^2=a^2+b^2$ is a special case of the cosine theorem.

Example

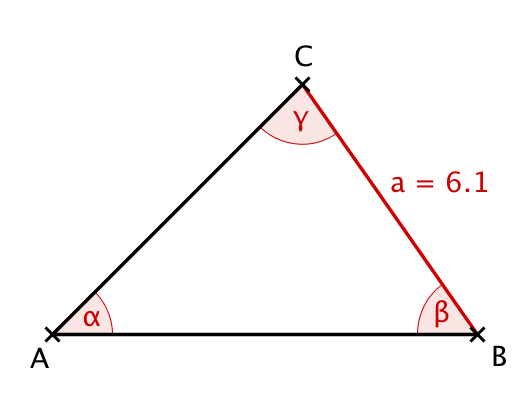
First calculate the length of side $b$ using the sine theorem:

$\frac{a}{\sin (\alpha )}=\frac{b}{\sin \left(\beta \right)}$ $\Rightarrow$ Plug in the known values.

$\frac{\mathrm{6,1}}{\sin \left({45}^{\circ }\right)}=\frac{b}{\sin \left({55}^{\circ }\right)}$ $\Rightarrow$ Solve for $b$ .

$\Rightarrow b=\frac{6.1\cdot \sin ({55}^{\circ })}{\sin ({45}^{\circ })}=7.1$

Now calculate the length of the side $c$ using the cosine theorem:

$c=\sqrt{a^2+b^2-2ab\cdot \cos \left(\gamma \right)}$ $\Rightarrow$ Plug in the values.

$=\sqrt{{6.1}^2+{7.1}^2-2\cdot 6.1\cdot 7.1\cdot \cos \left({80}^{\circ }\right)}=8.5$

Video