Linear Growth

In other words, the quantity changes by the same amount within equal time intervals. The linear growth function is given by a line equation:

$N(t)=a\cdot t+N_{0}N(t)=a\backslash cdot\; t+N\_0\backslash \backslash$

Here we have:

• $N\left(t\right)N\backslash left(t\backslash right)\backslash ;$ : the number or amount of $NN$ after time $tt$,

• $aa$         : the rate of change,

• $N_{0}N\_0$     : the number or amount of $NN$ at time $00$, i..e the initial value

Properties

• The growth rate or rate of change $aa$ is constant for linear growth or decay: $a\in \mathbb{R}a\backslash in\backslash mathbb\{R\}$.

• It corresponds to the slope of the graph of the linear growth function.

• Monotonicity: If $a>0a>0$, we speak of linear growth. The function is then strictly monotonically increasing.

• If , the function describes linear decay. The function is then strictly monotonically decreasing.

The graph of a linear growth function

As with linear functions, the rate of change $aa$ is calculated using a gradient triangle.

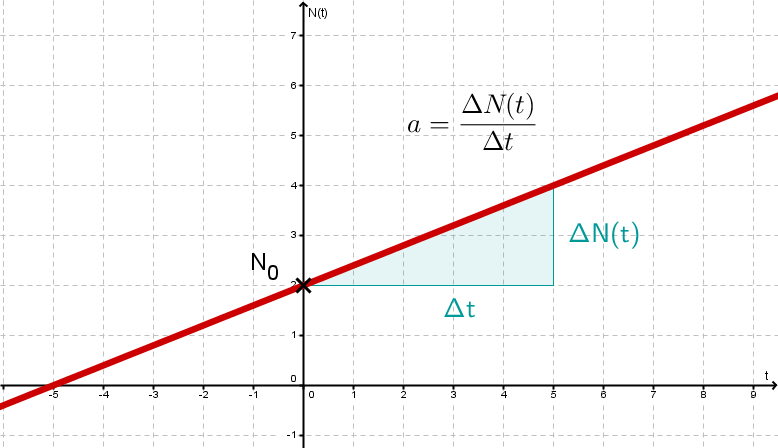
$\mathrm{\Delta }N(t)\backslash Delta\; N(t)$ denotes the difference of the values of $NN$ at two points in time.

In the figure, this is:

$\mathrm{\Delta }t\backslash Delta\; t$ stands for the period of time during which $NN$ is observed. In the figure:

Example

A tree is planted in a garden. At this point it protrudes $1m1m$ from the ground. After how many years will the tree be $5m5m$ high if it grows by $10cm10cm$ a year on average?

Solution:

First, write down the given and searched values from the data.

Required is the time $tt$ at which the tree has reached the size $5m5m$.

Given is the size of the tree at the beginning (= starting value $N_{0}N\_0$), its growth rate (= rate of change $aa$) and its size reached after $tt$ years (= $N(t)N(t)$).

(Note: t is given in years, $NN$ is the size of the tree in metres.

The tree grows $10cm10cm$ per year, therefore the unit of $a:\frac{cm}{\mathrm{y}ear}a:\backslash ;\backslash frac\{cm\}\{\backslash mathrm\; year\}$).

$N_0=1mN\_0=1m$

$a=10\frac{cm}{\mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}}=0.1\frac{m}{\mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}}a=10\backslash frac\{cm\}\{\backslash mathrm\{year\}\}=0.1\backslash frac\{m\}\{\backslash mathrm\{year\}\}$

$N\left(t\right)=5mN\backslash left(t\backslash right)=5m$

Now substitute the given values into the functional equation $N(t)=a\cdot t+N_{0}N(t)=a\backslash cdot\; t+N\_0$ and solve the equation for the $tt$ we are looking for.

Answer: After 40 years the tree is $5m5m$ high.