Difference Quotient

The difference quotient between two points $x_1$ and $x_2$ describes the slope of the secant between two points.

Geogebra File: https://assets.serlo.org/legacy/2733_aKZ05x7t30.xml

The difference quotient between two points $x_1$ and $x_2$ describes the slope of the secant between the points $P\left(x_1 \mid f(x_1)\right)$ and $Q\left(x_2 \mid f(x_2)\right)$ :

\displaystyle \frac{f(x_2)-f(x_1)}{x_2 - x_1}.

The difference quotient specifies the mean rate of change.

By taking the limit value, one obtains the differential quotient, which can later be used to compute the derivative of a function (= local rate of change).

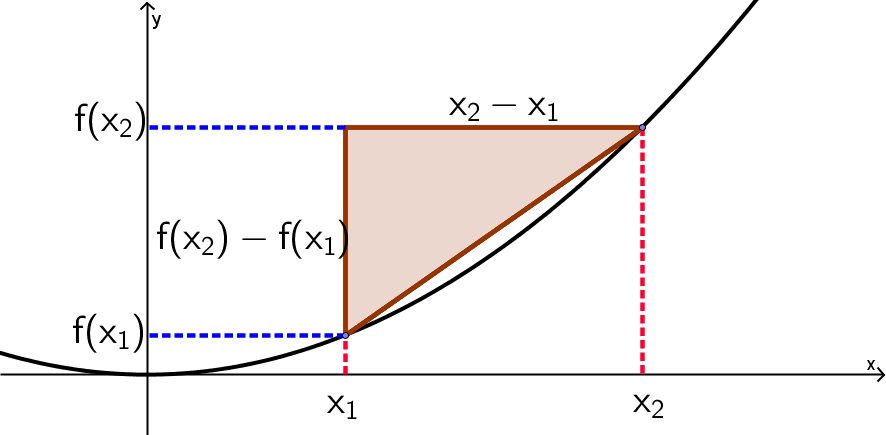
Example

Determine the difference quotient of the function $f(x)=x^2$ in the interval $\left[1;3\right]$ $\Rightarrow x_1=1$ and $x_2=3$ .

\displaystyle \frac{f(x_2)-f(x_1)}{x_2 - x_1}.

Video about the difference quotient

Content is loading…

Content:

0:00 - 0:27 : Intro

0:27 - 4:23 : General description of the mean rate of change

4:23 - 7:57 : Exemplary calculation of the mean rate of change

This video was created by "Quatematik" and was published on his channel on Youtube.

This work is available under the free licence CC BY-SA 4.0.Information

Applet

In the following applet you can look at the difference quotient for any function $f$ and have it calculated. You can also freely select the position of $x_1$ and $x_2.$

By clicking on image or button above you agree that external content from GeoGebra will be loaded. Also personal data may be transferred to this service in accordance with our Privacy Policy.

[https://www.geogebra.org/material/iframe/id/nnrmthf4]

This content is licensed under
CC BY-SA 4.0 → Info