Slope/Gradient of a Line
This article deals with straight lines as graphs of linear functions.
This article deals with straight lines as graphs of linear functions, i.e. functions of the form .
The m in the equation above is called the slope of the straight line.
The slope of a straight line indicates by how many units the -coordinate of a point changes when its -coordinate changes by one unit. In other words, the slope of a straight line measures how steeply it rises.
Calculating the line slope
The gradient/slope of a straight line can be determined from two different points and , which lie on the straight line, using the difference quotient:
It does not matter which points you choose, the quotient always has the same value.
Example
Determine the slope of the given line. To do this, select two points, for example and as in the sketch. The triangle drawn is called a gradient triangle.

One determines and , i.e. the difference of the -coordinates and -coordinates of the given points ...
... plugs in the values for the lengths of and into the formula.
So the line has the slope:
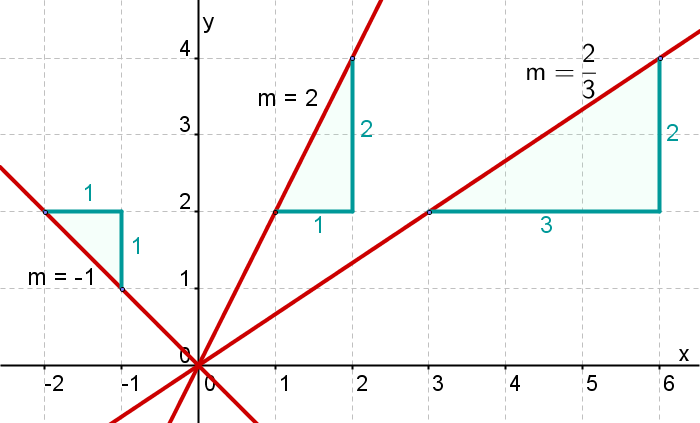
From the slope to the gradient triangle
Take any two points of the straight lines in the coordinate system and draw lines between them parallel to the coordinate axes. Those lines enclose a right-angled triangle.
Slope means:
"Go from a point on the line 1 length unit to the right and 2 length units upwards".
Slope means:
"Go from a point on the line 1 length unit to the right and 1 length unit downwards".
Slope means:
"Go from a point on the line 3 length units to the right and 2 length units upwards".
Slope means:
"Go from a point on the line 3 length units to the right and 2 length units downwards".
From the gradient triangle to the slope
If two points of the straight line are given, a gradient triangle can be drawn between them.
The slope of the straight line is then the length of the vertical cathetus (opposite cathetus) divided by the length of the horizontal cathetus (adjacent cathetus). The slope is positive if the straight line rises and negative if the straight line falls.
This results in the same equation as above:
Perpendicular and parallel lines
Consider two lines with their two line equations
Parallel lines
If
then both lines are parallel.
Perpendicular lines
If
then both lines are perpendicular.
Example:
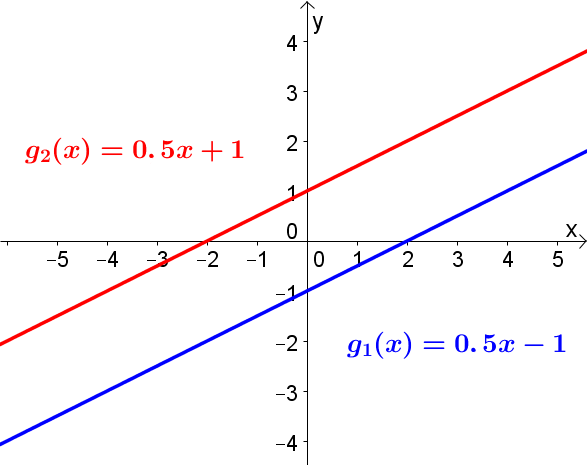
Example:

Angle of inclination
The angle of inclination indicates the angle of a straight line with respect to the -axis. The angle of inclination of a straight line satisfies
Slope of special straight lines
The slope of a straight line that is parallel to the -axis is .
In this case, the associated function is constant.
An equation for such a function would be .

The slope of a straight line parallel to the -axis would be "infinite".
However, there can be no function as a function of with such a straight line as a graph, since different -values would have to be assigned to the same -value.
Nevertheless, such a straight line can be described by an equation of the form .
