Gradient and Angle of Inclination
The gradient/slope of a function is a measure of how steeply the graph of a function rises or falls.
Mathematically, the slope can be described as the ratio of the deviation in the -direction to the deviation in the -direction.
From the slope m, one obtains the angle of inclination with the help of the tangent via:
Calculating the gradient
For lines
In a general equation of a straight line, the gradient is usually called .
It can be calculated using two points and the difference quotient:
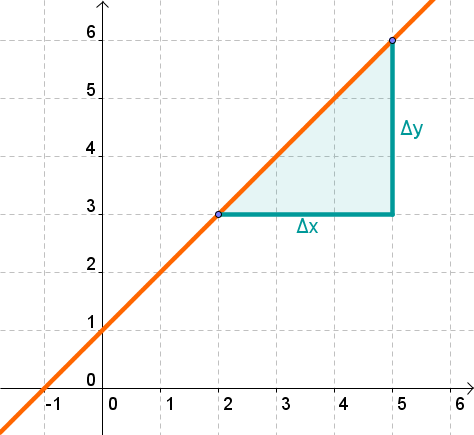
Further information and sample exercises are available in the article Slope/Gradient of a line.
For graphs at a given point
The slope of a general function can be different at each point. The slope at a point means the slope of the tangent line at that point.
This is described by the value of the first derivative at this point.
The derivative article deals with this in more detail.

Angle of inclination
The angle of inclination indicates the angle of a straight line to the -axis.
