Line Equation

A line is the infinite extension of the shortest connection between two points. Visually, a line is an infinitely long, straight line. There is always exactly one straight line between two points.

All straight lines can be represented by a linear equation, therefore straight lines are also called linear functions .

This article deals with straight lines in ordinary analysis. For straight lines in analytic geometry see: Article on the subject

General line equation

To set up the straight line, you only need the slope and the intersection of the straight line with the $y$ -axis.

y = m \cdot x + t

In this equation, $m$ is the slope of the straight line and $m$ is the $y$ -value where the straight line intersects the $y$ -axis.

Constituents of a line equation

A straight line equation consists of a gradient and the $y$ -axis intercept $t$ . These components are explained in more detail below.

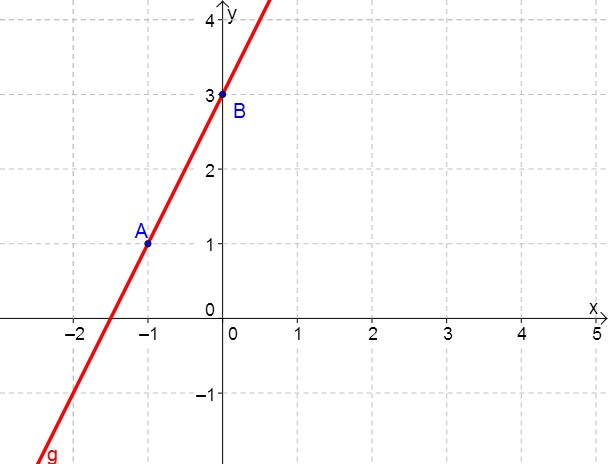
As an example consider the line:

y = 2 x + 3

Slope/Gradient

The slope indicates how steep a straight line climbs or falls. From the given equation, one can read out the gradient $m = 2$ .

If you did not know this, you can also determine the gradient using a gradient triangle. To do this, you need at least two different points, which you can obtain by inserting different $x$ -values.

The $y$ -axis intercept $t$

The $y$ -axis intercept $t$ indicates the $y$ -value at which the straight line intersects the $y$ -axis. The value is also obtained by inserting zero for $x$ into the equation of the straight line, since $m \cdot x$ is omitted for the case $x = 0$ and only $y = t$ remains from the original equation.

The fact that the $y$ -axis intercept $t$ has the value 3 in the example can also be seen in the drawing from the line intersecting the $y$ -axis at point $B$ . $B$ has the coordinates $(0 | 3)$ .

Calculate the equation of a line through two points

Example: Given are the points $A (- 1 | 1)$ and $B (2 | 3)$ . Calculate the equation of the straight line that passes through $A$ and $B$ .

Calculate the slope using the difference quotient $m = \frac{1 - 3}{- 1 - 2} = \frac{- 2}{- 3} = \frac{2}{3}$
Plug $m$ and any point into the equation of the line to determine $t$ . We use the point $B$ .
$\begin{array}{l} \begin{array}{ccccc} y & = & m \cdot x + t \\ 3 & = & \frac{2}{3} \cdot 2 + t & | - \frac{4}{3} \\ 3 - \frac{4}{3} & = & t \end{array} \\ \begin{array}{ccc} t & = & \frac{5}{3} \end{array} \end{array}$
Substitute $m$ and $t$ into the general equation of a line. $\Rightarrow y = \frac{2}{3} x + \frac{5}{3}$

Calculate the equation of the straight line given the $y$ -axis intercept $t$ and a point $P$ .

Example: Given are the $y$ -axis intercept $t = - 3$ and the point $P (2 / 1)$ . Calculate the corresponding equation of a straight line.

1. Insert $t$ and the coordinates of the point $P$ into the general line equation and solve for $m$ .

\begin{array}{l} \begin{array}{ccccc} y & = & m \cdot x + t \\ 1 & = & m \cdot 2 - 3 & | + 3 \\ 1 + 3 & = & m \cdot 2 | : 2 \end{array} \\ \begin{array}{ccc} m = 2 \end{array} \end{array}

2. Substitute $m$ and $t$ into the general equation of a straight line $\Rightarrow y = 2 x - 3$

General lines (interaktive)

By clicking on image or button above you agree that external content from GeoGebra will be loaded. Also personal data may be transferred to this service in accordance with our privacy policy.

Special lines

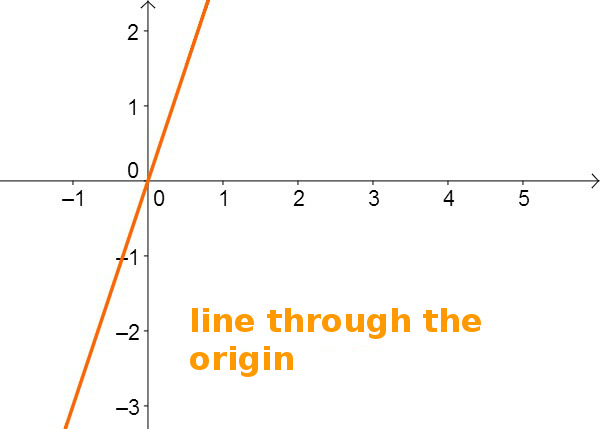
Lines through the origin

Such a straight line always has the equation $y = m \cdot x$ , since $t = 0$ holds.

A line through the origin may also represent a direct proportionality.

Constant function

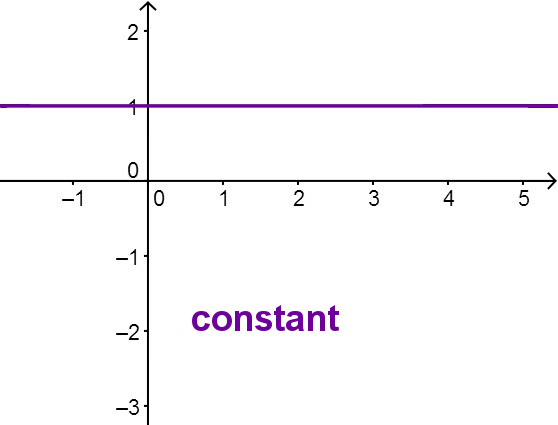
A line that is parallel to the $x$ -axis has the form $y = c$ and is the line of a constant function because it always takes the same, constant value.

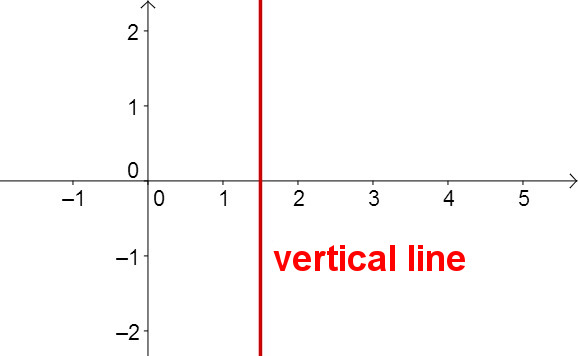
Vertical line

A line parallel to the $y$ -axis does not correspond to a function (see definition of a function), but to a relation. It cannot be described with the general equation of a straight line because the gradient would be infinite.

An equation for a vertical line has the form $x = c$ .

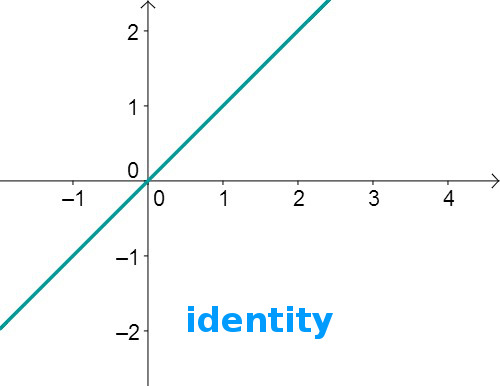
The identity line

The line through the origin corresponding to the function $y = x$ is called the identity line. It is the bisector of the first and third quadrants of the coordinate system.

This content is licensed under
CC BY-SA 4.0 → What does that mean? serlo.org