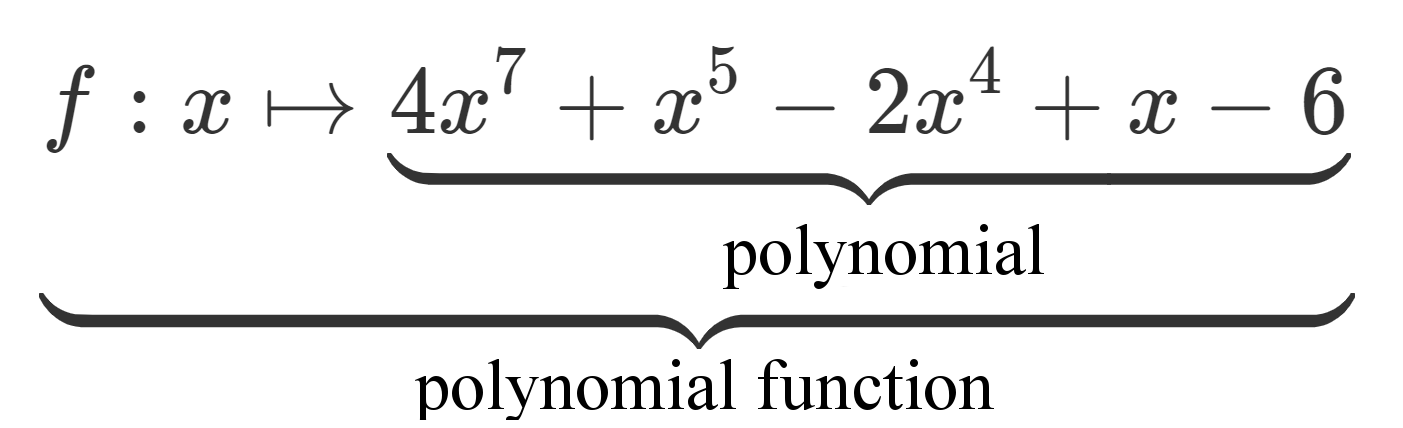
Polynomial

A Polynomial is an expression that:

Is made up of 2 or more algebraic terms
Especially the sum of several terms that contain different powers of the same variable(s)

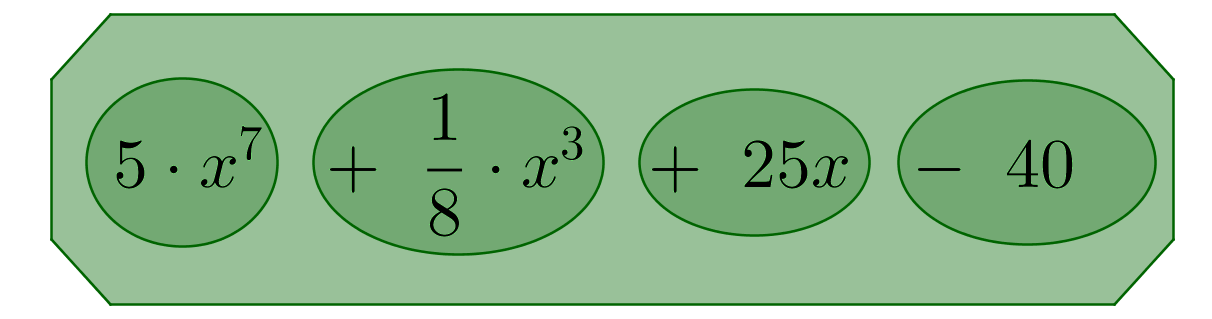
Examples of Polynomials:

Powers of the variable x multiplied by real numbers are called monomials (circled in darker green in the graph). These are added together as a sum to form the polynomial (in the square green box).

In a polynomial the multiples of several power functions are added, whose exponents come from the set {N} (natural numbers).

Examples for Polynomials:

$x^3-2x^2+x-4$
$8x^5+3x^3-x^2+12$
$4x^7+x^5-2x^4+x-6$

Mathematical Definition

Mathematically, a polynomial is a term that can be written in the following form:

$a_n\cdot x^n+a_{n-1}\cdot x^{n-1}+\dots+a_1\cdot x+a_0$

Where x is the variable, $a_n, a_{n-1}, …a_1, a_0$ are real numbers( $a_n\neq0$ ), and $n$ is a natual number.

Example

$4x^7+x^5-2x^4+x-6$

$\Rightarrow\$ here is $n=7$ , $a_7=4$ , $a_5=1$ , $a_4=-2$ , $a_1=1$ , $a_0=-6$

Ordered Polynomials

Usually a polynomial is written down in an ordered way. A polynomial is called "ordered" if the polynomial is summarized and sorted by falling exponents.

So not in the form of $2x^2+1- x^7$ ,but like this $\phantom{}-x^7+2x^2+1$ .

Degree of the polynomial

The degree of the polynomial is the highest occurring power.

So we here we have a few examples…

$x^{\textcolor{ff6600}{3}}-2x^2+x-4$ den Grad $\textcolor{ff6600}{3}$ ,
$8x^{\textcolor{ff6600}{5}}+3x^3-x^2+12$ den Grad $\textcolor{ff6600}{5}$ und
$4x^{\textcolor{ff6600}{7}}+x^5-2x^4+x-6$ den Grad $\textcolor{ff6600}{7}$ .

The function of the Polynomial:

A function $f$ : $x\mapsto f(x)$ , written as $f(x)$ is a polynomial, is called an integer function or polynomial function.

You can find more information about the features and properties of such a function in the article : Integer functions (polynomial functions).

This content is licensed under
CC BY-SA 4.0 → Info