Polynomial Functions
A function : , whose function term is a Polynomial, is called an integral function or polynomial function.
Thus a "-th" integer function is a function of the form.

The numbers are known as .
These numbers are known as .
The largest occuring exponent (here: ) determines the degree of the polynomial function.
The coefficient before the largest occurring exponent is called the leading coefficient(here: ).
Example
The coefficients are ; and .
The exponents occurring are und
has the degree and the conducting coefficients .
The Zero
An integer function of the nth degree has at most n zero points.
For polynomial functions up to degree 2, solution formulas exist such as the Square solution formula.
At higher degrees, the Polynomial division, simplify a Polynomial if you already know a zero (e.g by guessing)
For 3rd and 4th degree polynomial functions, there are formulas (which are not commonly used in school and are complicated). For higher degrees, one cannot form a general formula for the zeros.
Limiting Values
If x is allowed to plus or minus infinitely, the limit value of the polynomial function is always plus or minus infinity of the polynomial function is always plus or minus infinity. The sign of the two limit values is the same for integer functions of even degree, and different for odd degree. The sign of the parameter with the highest power (called a in the table) determines the sign of the limit values.
Beispiele
Im Folgenden werden die Grenzwerte der Funktionen
und
für jeweils und betrachtet.
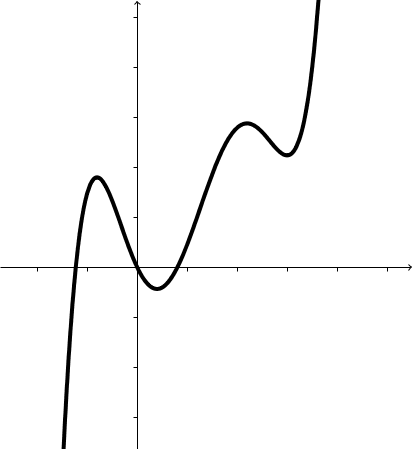
Ungerader Grad
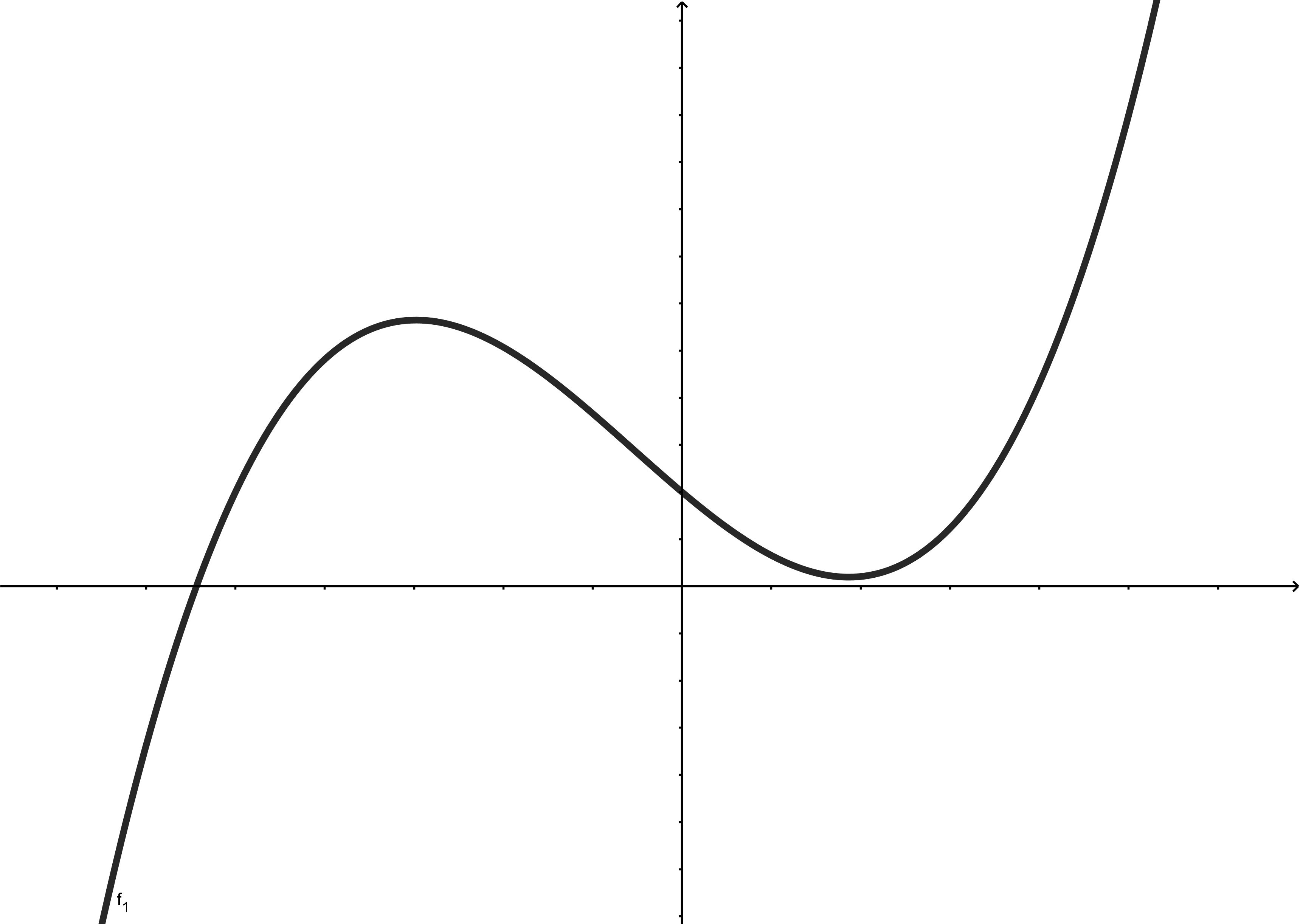
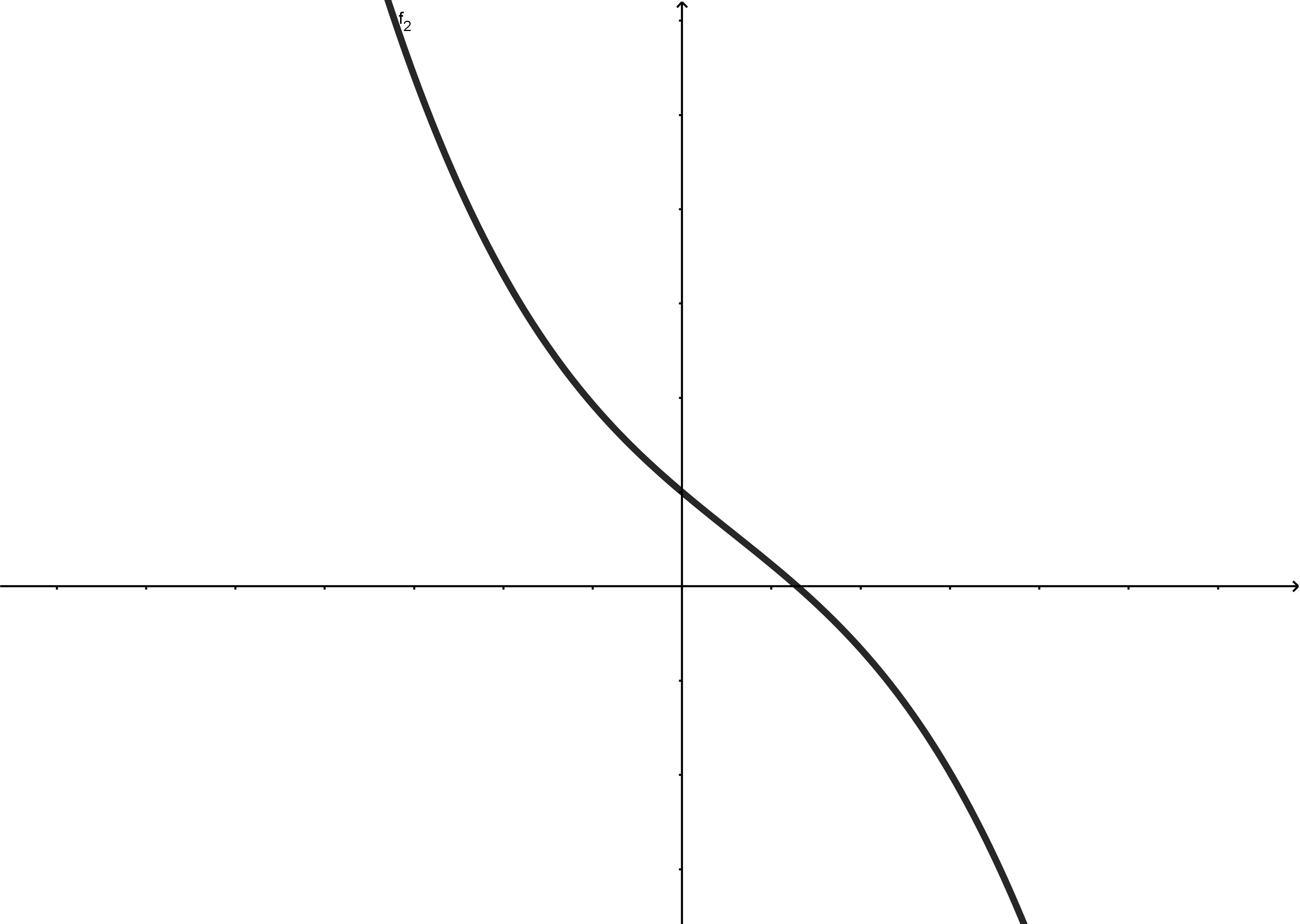
Gerader Grad
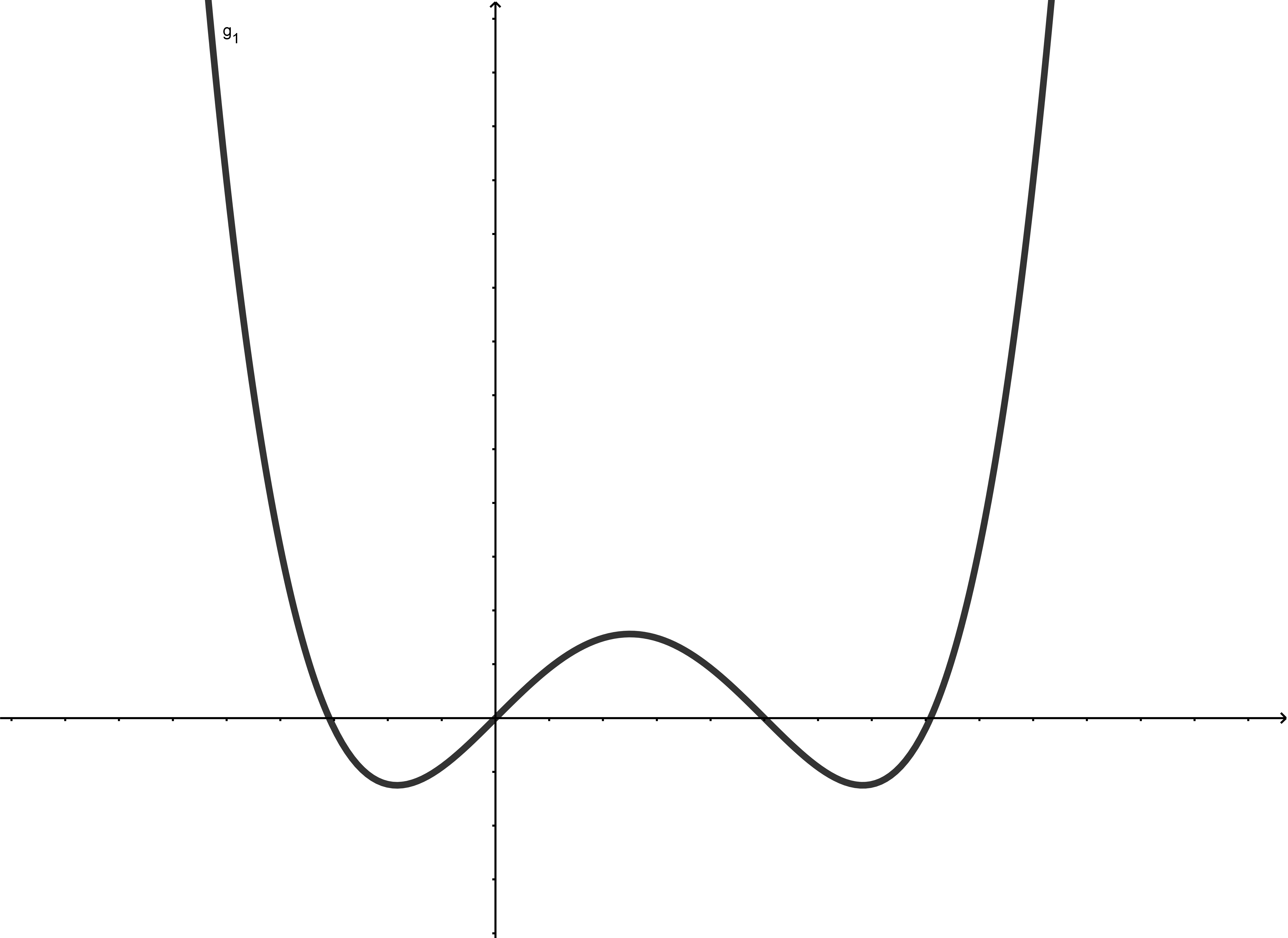
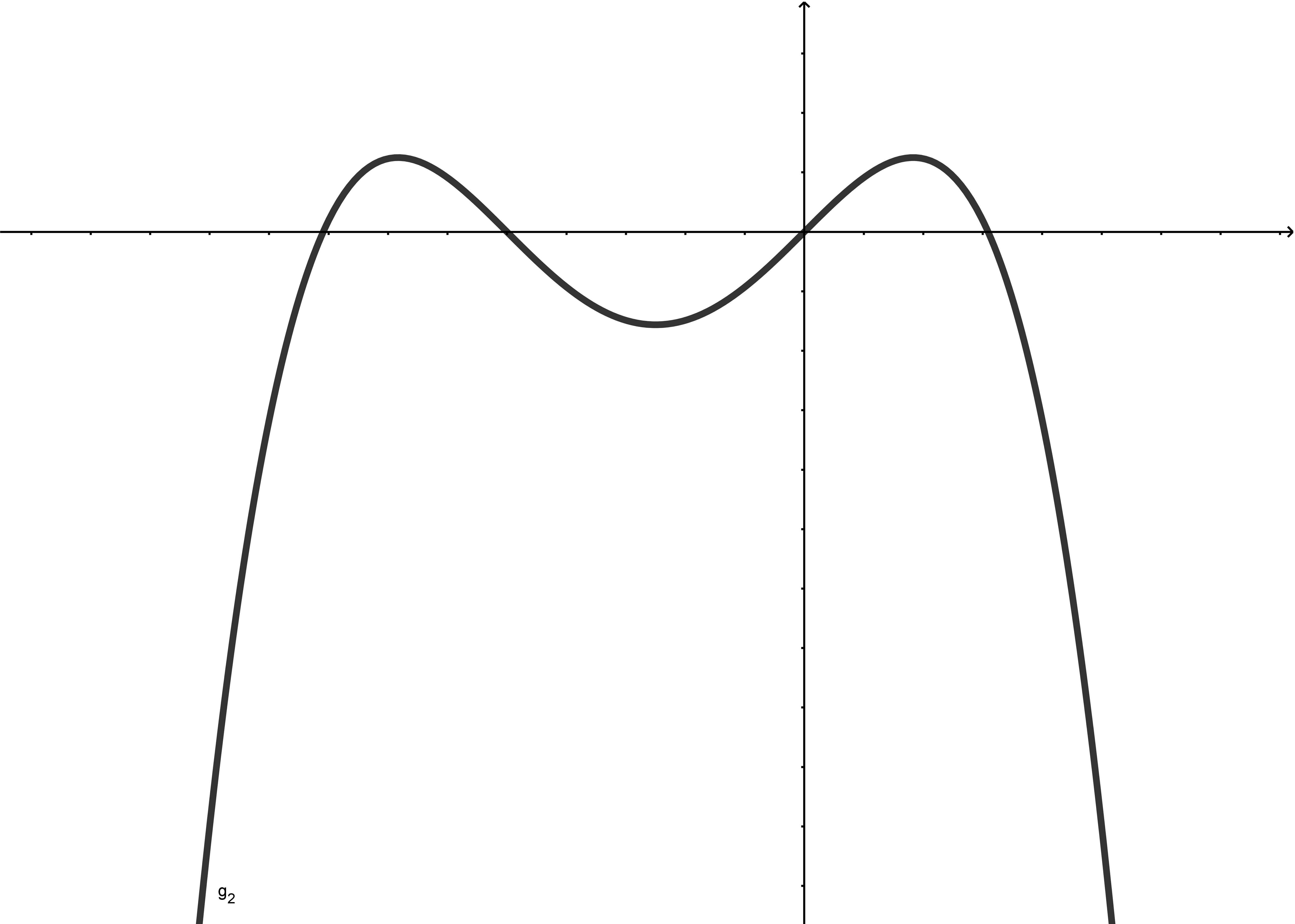
Spezielle Polynomfunktionen
Im Folgenden werden spezielle Polynomfunktionen vorgestellt:
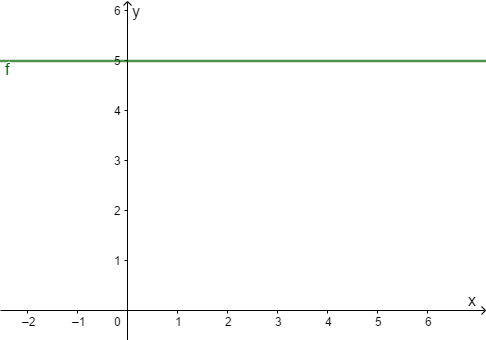
Konstante Funktionen (Grad 0)
Graph der Abbildung
Die Konstante Funktion ordnet jedem dasselbe zu.
Der Graph der konstanten Funktion ist eine Parallele zur -Achse, die die -Achse auf der Höhe schneidet.
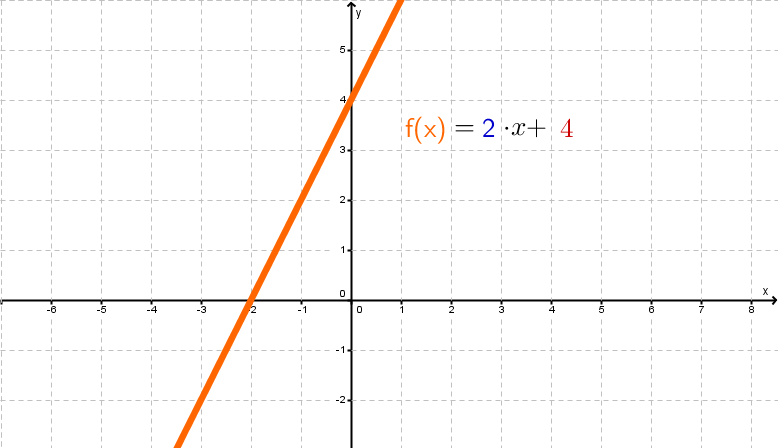
Lineare Funktionen (Grad 1)
Graph der Funktion
Lineare Funktionen sind ganzrationale Funktionen ersten Grades. Sie haben die Form
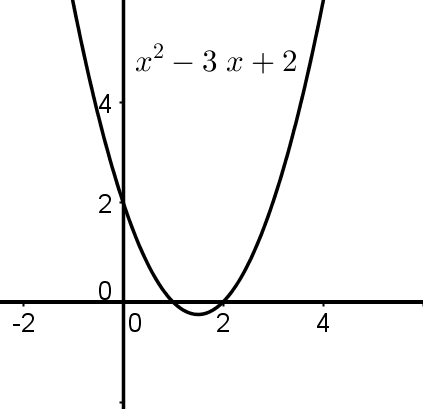
Quadratische Funktionen (Grad 2)
Graph der Funktion
Quadratische Funktionen sind Polynomfunktionen vom Grad 2. Sie haben die Form
Beispiele und Nicht-Beispiele


Extrema
Abbildung: Graph einer Polynomfunktion 5-ten Grades
Um die Extrema einer Polynomfunktion -ten Grades zu bestimmen, berechnet man zunächst die Ableitung und bestimmt davon die Nullstellen. ist eine Polynomfunktion -ten Grades. Diese hat maximal Nullstellen.
Also folgt:
Eine Polynomfunktion -ten Grades hat höchstens Extrema.