Method of Crossing off Fields
The "field skimming" is a method used to get an approximate view of the graph's history using only the zeros.
It is usually applied to polynomial functions.

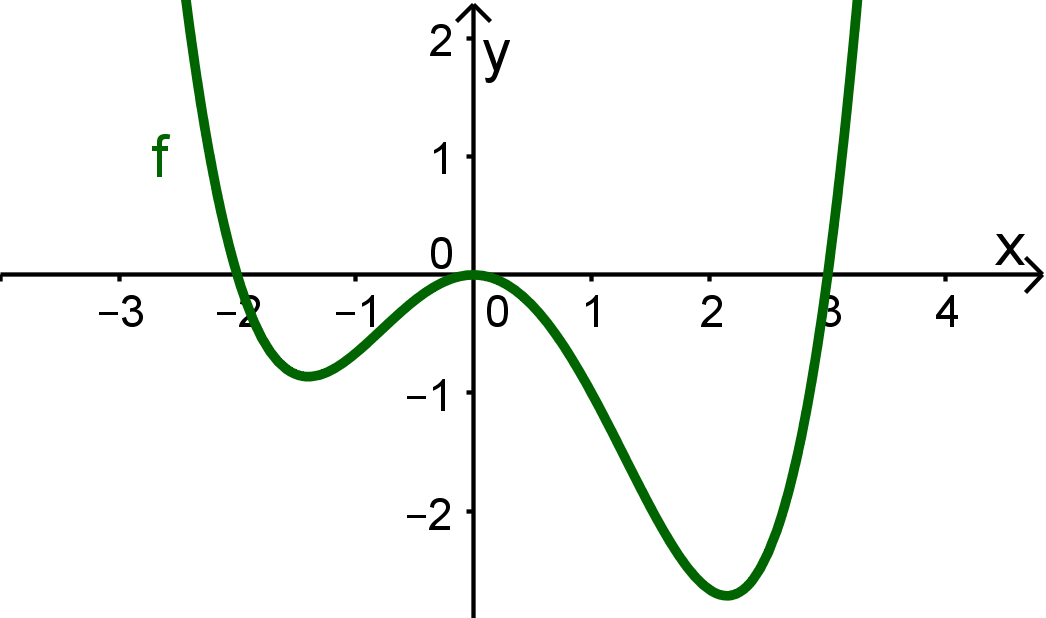
Function, given by function term
The graph from the Function
Procedure:
The following steps are used when crossing off fields:
Determine zeros of the function
Create coordinate system and delimit areas
Determine the sign of the function in the individual areas and mark the fields through which the graph runs or does not run. (cross of fields)
Draw the approximate course of the graph
Tips and details, procedure by example
First step: Determine zeros
First, you have to find the zeros of the function.
How this is done in detail depends, of course, on the function.
Sometimes the zeros are already given somewhere in the problem definition or have been calculated in a sub-task before.
If a polynomial function is given in linear factor representation, the zeros (and also their multiplicities) can be easily read from the function term.
Otherwise you have to calculate the zeros before you can continue.
Second step: Create graphic
Then,
you create a coordinate system,
enter the zeros,
and delimit the areas.
For this purpose, a thin auxiliary line perpendicular to the x-axis is drawn at the zeros as a "boundary line" between the ranges.
(In addition, one must draw such border lines at definition gaps and at jump points of the function; with polynomial functions, however, there are neither definition gaps nor jump points).
In the example:
Sketched coordinate system with the delimited areas:
Here lines are drawn at the zeros -2, 0 and 3 to delimit the ranges.
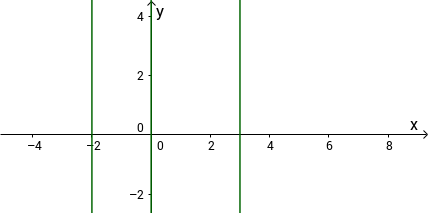
Third step: Determine the sign of the individual ranges, mark fields
Determine sign
Next, determine the sign of the function values in each of the rangese.
To do this, you simply need to insert an x-value into the function for each range..
For example:
für
für
für
für
For polynomial functions, the sign for the later ranges can also be inferred with the multiplicity of the zeros.
For example:
Mark fields
If one knows the signs, one usually crosses out for each area the field through which the graph certainly does not run, i.e.
the field below the x-axis, if the function values are positive
or the field above the x-axis, if the function values are negative.
For example:
in Progress:
Fourth step: draw a rough graph
After crossing out all the "forbidden" areas, freehand draw the approximate path of the graph through the "allowed" fields.
In Progress: