Exercises: Intersection of two lines
Consider the following graphs.
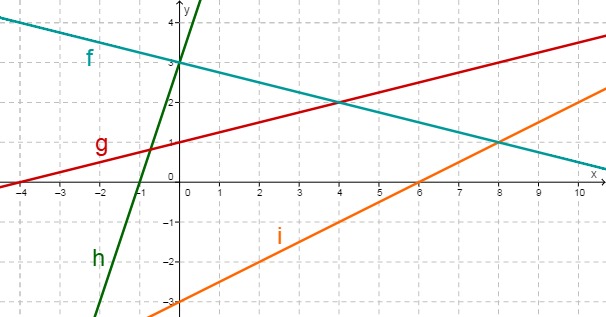
Determine the function equations of all 4 lines.
For this task you need the following basic knowledge: Line equation
Line equation of
In order to determine the line equation of , first read off two points from the diagram that lie on the straight line . In the above example, you may for instance get and . Use these two points to determine the slope of via the difference quotient
Plug in the values
Now determine the -axis intercept by plugging in any point on into the general line equation. Alternatively, you may directly read off at which value intersects the -axis (if possible).
For instance, plug in .
Simplify.
So the line equation is .
Line equation of
In order to determine the line equation of , first read off two points from the diagram that lie on the straight line . In the above example, you may for instance get and . Use these two points to determine the slope of via the difference quotient
Plug in the values
Now determine the -axis intercept by plugging in any point on into the general line equation. Alternatively, you may directly read off at which value intersects the -axis (if possible).
For instance, plug in .
Simplify.
So the line equation is .
Line equation of
In order to determine the line equation of , first read off two points from the diagram that lie on the straight line . In the above example, you may for instance get and . Use these two points to determine the slope of via the difference quotient
Plug in the values
Now determine the -axis intercept by plugging in any point on into the general line equation. Alternatively, you may directly read off at which value intersects the -axis (if possible).
For instance, plug in .
Simplify.
So the line equation is .
Line equation of
In order to determine the line equation of , first read off two points from the diagram that lie on the straight line . In the above example, you may for instance get and . Use these two points to determine the slope of via the difference quotient
Plug in the values
Now determine the -axis intercept by plugging in any point on into the general line equation. Alternatively, you may directly read off at which value intersects the -axis (if possible).
For instance, plug in .
Simplify.
So the line equation is .
Determine the intersection of g and h , and the zero of f.
Intersection point of and
To determine the point of intersection of two functions, you set them equal and solve for . The function equations (determined in the previous problem) are and .
↓ subtract and .
↓ divide by .
Now substitute into the line equation of or to determine .
Plug in .
The lines and therefore intersect at .
You may obtain the zero of by setting the function equation equal to 0 and solving for .
So has the zero 12.
Calculate the two intersections that lie outside the figure.
The intersection of and and the intersection of and lie outside the figure above.
Intersection point of and
To determine the point of intersection of two functions, you set them equal and solve for . The function equations (determined in the previous problem) are and .
Now substitute into the line equation of or to determine .
Plug in .
The lines and therefore intersect at .
Intersection point of and
To determine the point of intersection of two functions, you set them equal and solve for . The function equations (determined in the previous problem) are and .
Now substitute into the line equation of or to determine .
Plug in .
The lines and therefore intersect at .
What is the maximum number of intersections of four straight lines?
If no pair of lines is parallel, then there are a total of 6 intersections, namely the following:
and
and
and
and
and
and