Mixed exercises: Quadratic functions

Christian, Manfred und Peter sollten als Hausaufgabe die Gleichung $x^{2} - 2 x - 2 = 0$ graphisch lösen. Sie sind dabei unterschiedlich vorgegangen, aber alle auf die gleichen Näherungslösungen $x_{1} \approx - 0,7$ und $x_{2} \approx 2,7$ gekommen.

a. Überprüfe die Näherungslösungen rechnerisch.

b. Erläutere die Vorgehensweisen von Christian, Manfred und Peter.

c. Ermittle mit jedem Verfahren die Lösungen der Gleichung $x^{2} + 3 x + 2 = 0$ .

d. Manfred und Peter sind von Christians Methode begeistert und versuchen, damit die Gleichung $2 x^{2} - x - 6 = 0$ zu lösen.

Sie gehen dabei aber unterschiedlich vor (siehe nachstehende Abbildungen). Welche Ergebnisse erhalten sie? Überprüfe rechnerisch. Wer von beiden ist deiner Meinung nach geschickter vorgegangen? Begründe.

For this task you need the following basic knowledge: Quadratische Funktionen

Teilaufgabe a

Setze die Funktion gleich 0, um die Nullstellen zu bestimmen.

$x^{2} - 2 x - 2 = 0$

Nun kannst du die Mitternachsformel anwenden. Berechne hierfür die Diskriminante D.

$D = {(- 2)}^{2} - 4 \cdot 1 \cdot (- 2) = 12$

$\Rightarrow$ Die Diskriminante ist positiv, also hat die Gleichung $x^{2} - 2 x - 2 = 0$ zwei Lösungen.

Bestimme nun die Lösungen:

$x_{1} = \frac{2 + \sqrt{12}}{2} = 1 + \sqrt{3} \approx 2,7$

$x_{2} = \frac{2 - \sqrt{12}}{2} = 1 - \sqrt{3} \approx 0,7$

Teilaufgabe b

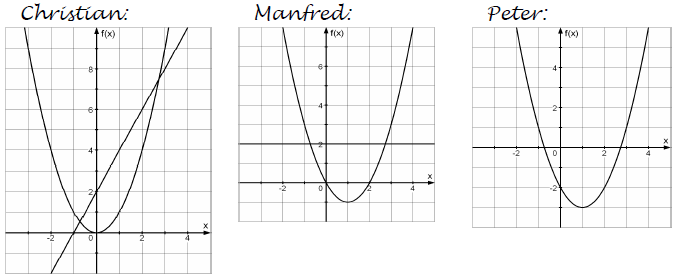
Vorgehen von Christian:

Christian bestimmt den Schnittpunkt einer Normalparabel $f (x) = x^{2}$ mit einer Geraden. Wir können die gegebene Gleichung wie folgt umformen:

$x^{2} - 2 x - 2$	$=$	$0$
$x^{2} - (2 x + 2)$	$=$	$0$	$+ (2 x + 2)$
$x^{2}$	$=$	$2 x + 2$

Christian zeichnet also eine Parabel mit dem Funktionsterm $f (x) = x^{2}$ und eine Geraden mit dem Funktionsterm $g (x) = 2 x + 2$ . Er liest dann deren Schnittpunkt ab.

Vorgehen von Manfred:

Manfred liest den Schnittpunkt einer konstanten Funktion mit einer Parabel ab. Er kommt auf diese Idee durch folgende Termumformungen:

$x^{2} - 2 x - 2$	$=$	$0$
	↓	Quadratische Ergänzung, um auf die Scheitelform zu kommen.
$x^{2} - 2 x + {(\frac{2}{2})}^{2} - {(\frac{2}{2})}^{2} - 2$	$=$	$0$
	↓	Binomische Formel anwenden.
${(x - 1)}^{2} - {(\frac{2}{2})}^{2} - 2$	$=$	$0$	$+ 2$
${(x - 1)}^{2} - 1$	$=$	$2$

Manfred zeichnet also eine Parabel mit dem Funktionsterm $f (x) = {(x - 1)}^{2} - 1$ und eine konstante Funktion mit dem Funktionsterm $g (x) = 2$ . Er liest dann deren Schnittpunkt ab.

Vorgehen von Peter:

Peter zeichnet eine Parabel und bestimmt die Nullstellen, indem er die Schnittpunkte mit der x-Achse abliest.

$x^{2} - 2 x - 2$	$=$	$0$
	↓	Quadratische Ergänzung, um auf die Scheitelform zu kommen.
$x^{2} - 2 x + {(\frac{2}{2})}^{2} - {(\frac{2}{2})}^{2} - 2$	$=$	$0$
	↓	Binomische Formel anwenden.
${(x - 1)}^{2} - 1 - 2$	$=$	$0$
${(x - 1)}^{2} - 3$	$=$	$0$

Peter zeichnet die Parabel mit dem Funktionsterm in Scheitelpunktsform $f (x) = (x - 1)^{2} - 3$ .

Teilaufgabe c

Bestimme nun graphisch die Lösung der Gleichung $x^{2} + 3 x + 2 = 0$ mit den verschiedenen Verfahren von Christian, Manfred und Peter.

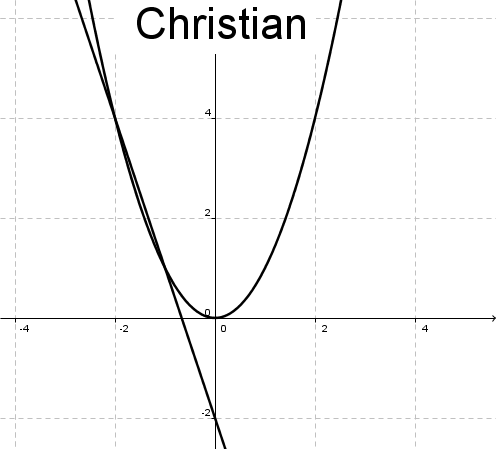
Christians Methode:

Christian bestimmt den Schnittpunkt einer Normalparabel $f (x) = x^{2}$ mit einer Geraden. Wir können die gegebene Gleichung wie folgt umformen:

$x^{2} + 3 x + 2$	$=$	$0$	$- 3 x - 2$
$x^{2}$	$=$	$- 3 x - 2$

Christian setzt die Normalparabel einer Geraden gleich, um so den Schnittpunkt zu berechnen.

Er erhält so die Lösungen $x_{1} \approx - 2$ und $x_{2} \approx - 1$ .

Manfreds Methode:

Manfred liest den Schnittpunkt einer konstanten Funktion mit einer Parabel ab. Er kommt auf diese Idee durch folgende Termumformungen:

$x^{2} + 3 x + 2$	$=$	$0$
	↓	Quadratische Ergänzung, um auf die Scheitelform zu kommen.
$x^{2} + 3 x + {(\frac{3}{2})}^{2} - {(\frac{3}{2})}^{2} + 2$	$=$	$0$
${(x + \frac{3}{2})}^{2} - {(\frac{3}{2})}^{2} + 2$	$=$	$0$
	↓	Binomische Formel anwenden.
${(x + \frac{3}{2})}^{2} - \frac{9}{4} + 2$	$=$	$0$	$- 2$
${(x + \frac{3}{2})}^{2} - \frac{9}{4}$	$=$	$- 2$

Manfred liest so die Lösungen $x_{1} = - 1$ und $x_{2} = - 2$ ab.

Peters Lösung:

Peter zeichnet eine Parabel und bestimmt die Nullstellen, indem er die Schnittpunkte mit der x-Achse abliest.

$x^{2} + 3 x + 2$	$=$	$0$
	↓	Quadratische Ergänzung, um auf die Scheitelform zu kommen.
$x^{2} + 3 x + {(\frac{3}{2})}^{2} - {(\frac{3}{2})}^{2} + 2$	$=$	$0$
${(x + \frac{3}{2})}^{2} - {(\frac{3}{2})}^{2} + 2$	$=$	$0$
	↓	Binomische Formel anwenden.
${(x + \frac{3}{2})}^{2} - \frac{9}{4} + 2$	$=$	$0$
	↓	Hauptnenner bilden.
${(x + \frac{3}{2})}^{2} - \frac{9}{4} + \frac{8}{4}$	$=$	$0$
${(x + \frac{3}{2})}^{2} - \frac{1}{4}$	$=$	$0$

Peter liest die Nullstellen $x_{1} = - 2$ und $x_{2} = - 1$ ab.

Teilaufgabe d

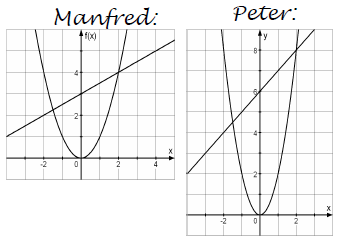
Manfred:

Manfred ging wie folgt vor:

$2 x^{2} - x - 6$	$=$	$0$	$+ x + 6$
$2 x^{2}$	$=$	$x + 6$	$: 2$
$x^{2}$	$=$	$\frac{1}{2} x - 3$

Manfred teilt durch 2, um die Normalparabel zu erhalten und damit die Gerade zu schneiden.

Peter:

Peter macht dies nicht, sondern zeichnet die Parabel gleich mit der Stauchung um 2. Genauso wie Manfred findet er durch das Schneiden mit der Gerade die Lösung der Gleichung.

$\Rightarrow$ Manfreds Methode ist praktischer, da sich eine Normalparabel einfacher zeichnen lässt als eine mit Stauchung.

This content is licensed under
CC BY-SA 4.0 → What does that mean? serlo.org