Mixed exercises: Quadratic functions
Gegeben sind die quadratischen Funktionen und mit und
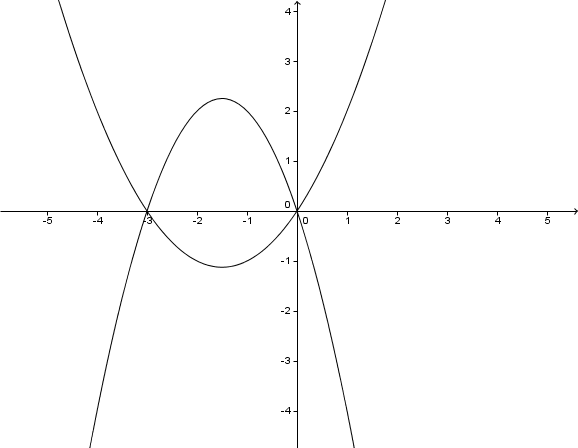
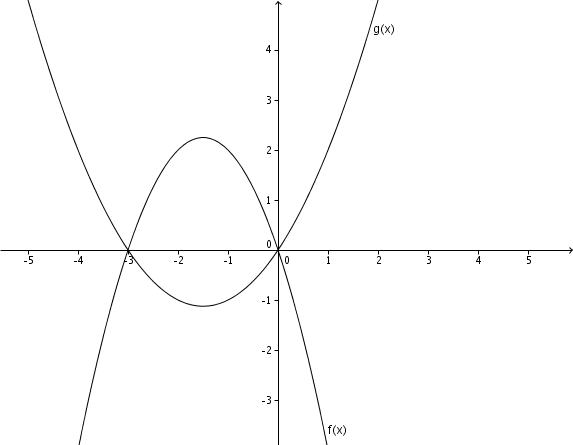
Zeichne die Graphen von und in ein Koordinatensystem. Begründe ohne Rechnung, warum sich und auf der x-Achse schneiden.
ist der Scheitel von .
Gib den Scheitel von an.
Die Gerade schneidet den Graphen von im Punkt und den Graphen von im Punkt . Gib und an.
Für ist die Strecke [PQ] eine Seite eines Rechtecks, das den beiden Parabeln einbeschrieben ist. Bestimme den Inhalt des Rechtecks für und den Umfang in Abhängigkeit von .
Im Bild ist :
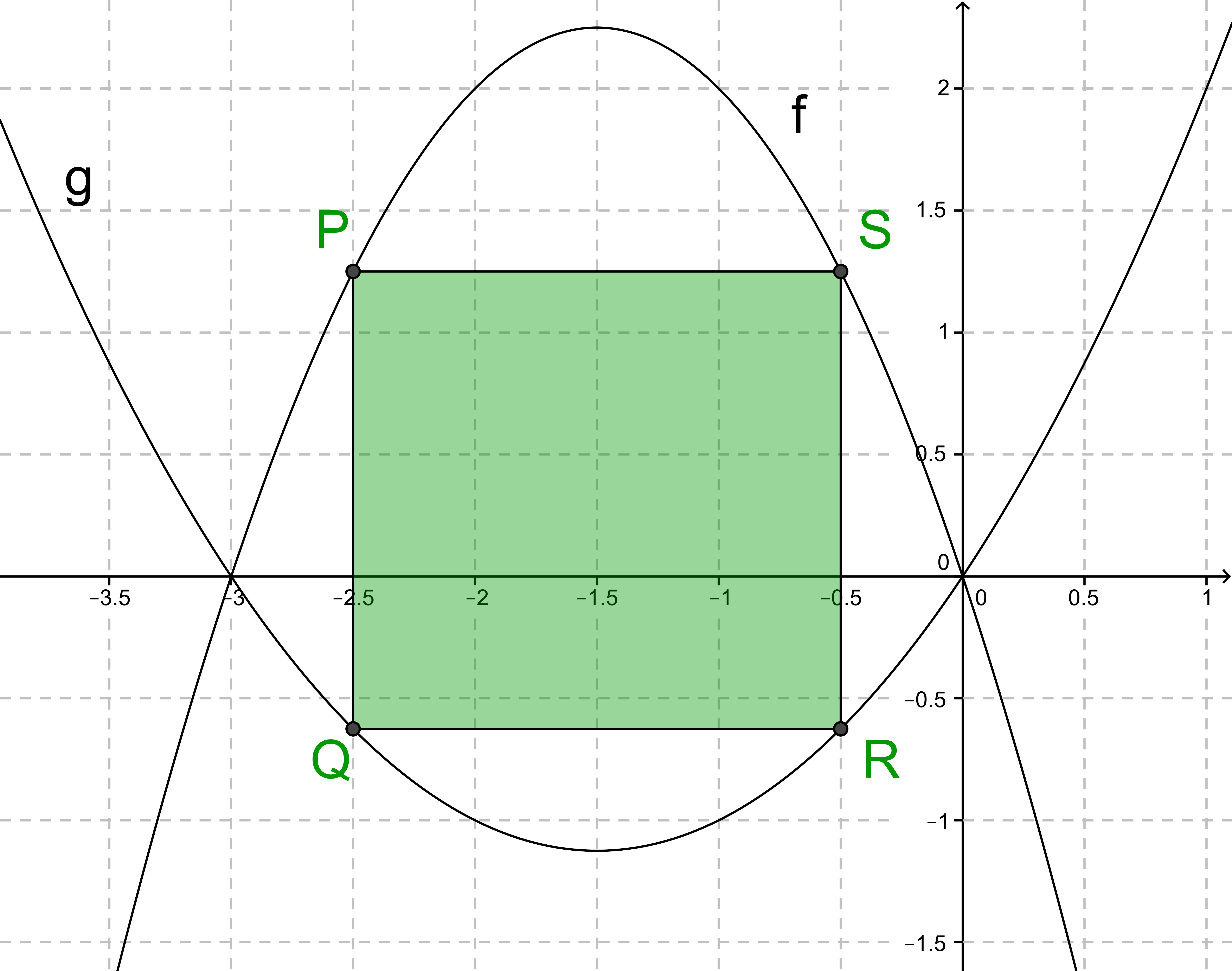
Verschiebe die Parabel in y-Richtung so, dass die verschobene Parabel den Graphen von berührt. Bestimme die Koordinaten des Berührpunktes .
Bestimme so, dass ist.