Mixed exercises: Quadratic functions
Gegeben sind die Funktionsgleichungen folgender Parabeln:
1.Bestimme die Scheitelform und den Scheitelpunkt.
2.Berechne die Achsenschnittpunkte.
3.Beschreibe schrittweise, wie f(x) aus der Normalparabel entsteht und wie sie geöffnet ist.
4.Zeichne den Graphen von f(x) in ein geeignetes Koordinatensystem.
1.Scheitelpunkt berechnen
↓ In die Scheitelform umwandeln. Dazu die quadratische Ergänzung machen.
↓ Umformen in eine Binomische Formel .
2.Achsenschnittpunkte berechnen
Schnittpunkte mit der x-Achse
↓ Nullstelle berechnen. Die Gleichung gleich 0 setzen.
↓ Mitternachtsformel anwenden. Dazu zuerst die Diskriminante D berechnen.
2 Lösungen
Schnittpunkte mit der y-Achse
↓ Für x gleich 0 setzen.
3.Verschiebung
Normalparabel:
Die verschiedenen Verschiebungen lassen sich an der Scheitelform ablesen.
Verschiebung um 2 LE nach rechts.
Verschiebung um 2 LE nach unten.
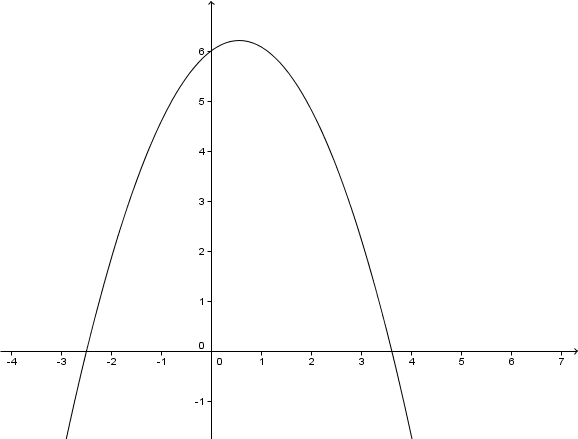
4.Zeichnung
1.Scheitelpunkt berechnen
↓ In die Scheitelform umwandeln. Dazu die quadratische Ergänzung machen.
↓ Umformen in eine Binomische Formel.
2.Achsenschnittpunkte berechnen
Schnittpunkte mit der x-Achse
↓ Nullstelle berechnen . Die Gleichung gleich 0 setzen.
↓ Mitternachtsformel anwenden. Dazu zuerst die Diskriminante D berechnen.
2 Lösungen
Schnittpunkt mit der y-Achse
↓ Für x gleich 0 setzen.
3.Verschiebung des Funktionsgraphen
Normalparabel:
Die verschiedenen Verschiebungen lassen sich an der Scheitelform ablesen.
Verschiebung um 2 LE nach links.
Verschiebung um 2 LE nach unten.
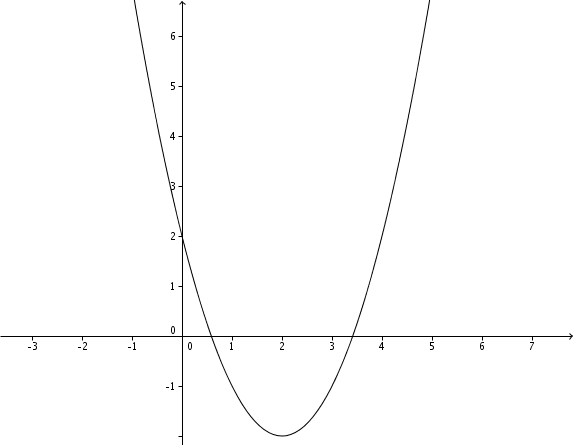
4.Zeichnung
1.Scheitelpunkt berechnen
↓ Minus ausklammern. Distributivgesetz.
↓ Umformen in eine Binomische Formel.
↓ Distributivgesetz anwenden.
2.Achsenschnittpunkte berechnen
Schnittpunkte mit der x-Achse
↓ Nullstelle berechnen. Die Gleichung gleich 0 setzen.
↓ Mitternachtsformel anwenden. Dazu zuerst die Diskriminante D berechnen.
2 Lösungen
Mit Taschenrechner den genauen Wert berechnen.
Mit Taschenrechner den genauen Wert berechnen.
Schnittpunkt mit der y-Achse
↓ Für x gleich 0 setzen.
3.Verschiebung des Funktionsgraphen
Normalparabel:
Die verschiedenen Verschiebunge n lassen sich an der Scheitelform ablesen.
Nach unten geöffnet.
Verschiebung um 2 LE nach links.
Verschiebung um 7LE nach oben.
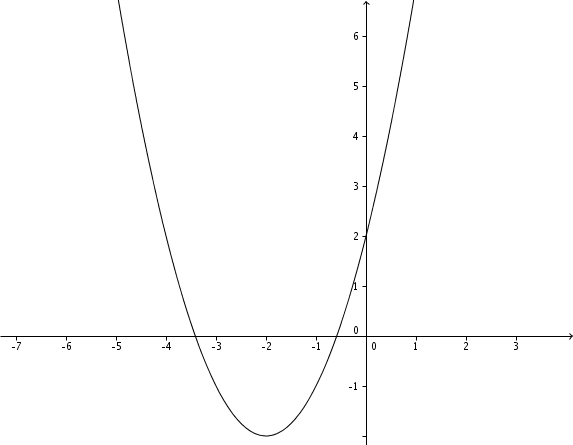
4.Zeichnung
1.Scheitelpunkt berechnen
↓ Minus ausklammern. Distributivgesetz.
↓ In die Scheitelform umwandeln. Dazu die quadratische Ergänzung machen.
↓ Umformen in eine Binomische Formel .
↓ Distributivgesetz anwenden.
2.Achsenschnittpunkte berechnen
Schnittpunkte mit der x-Achse
↓ Nullstelle berechnen. Die Gleichung gleich 0 setzen.
↓ Mitternachtsformel anwenden. Dazu zuerst die Diskriminante D berechnen.
2 Lösungen
Mit Taschenrechner den genauen Wert berechnen.
Mit Taschenrechner den genauen Wert berechnen.
Schnittpunkte mit der y-Achse
↓ Für x gleich 0 setzen.
3.Verschiebung des Funktionsgraphen
Normalparabel:
Die verschiedenen Verschiebungen lassen sich an der Scheitelform ablesen.
Nach unten geöffnet.
Verschiebung um 4 LE nach rechts.
Verschiebung um 7 LE nach oben.
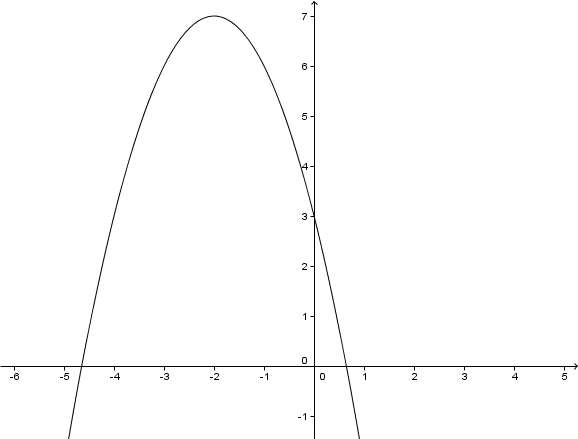
4.Zeichnung
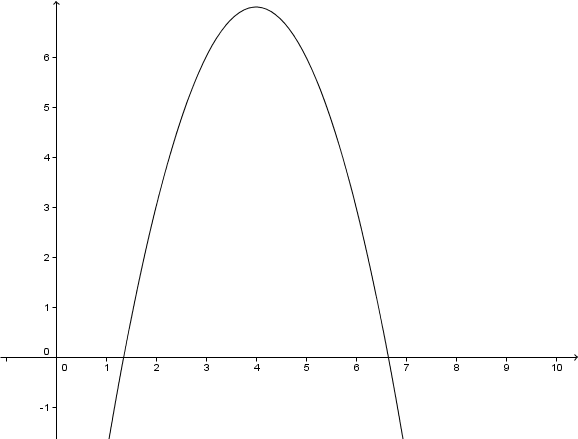
1.Scheitelpunkt berechnen
↓ ausklammern. Distributivgesetz .
↓ In die Scheitelform umwandeln. Dazu die quadratische Ergänzung machen.
↓ Umformen in eine Binomische Formel .
↓ Distributivgesetz anwenden.
2.Achsenschnittpunkte berechnen
Schnittpunkte mit der x-Achse
↓ Nullstelle berechnen. Die Gleichung gleich 0 setzen.
↓ Mitternachtsformel anwenden. Dazu zuerst die Diskriminante D berechnen.
2 Lösungen
Mit Taschenrechner den genauen Wert berechnen.
Mit Taschenrechner den genauen Wert berechnen.
Schnittpunkte der y-Achse
↓ Für x gleich 0 setzen.
3.Verschiebung des Funktionsgraphen
Normalparabel:
Die verschiedenen Verschiebungen lassen sich an der Scheitelform ablesen.
Gestaucht mit .
Verschiebung um 4 LE nach rechts.
Verschiebung um 3LE nach unten.
4.Zeichnung
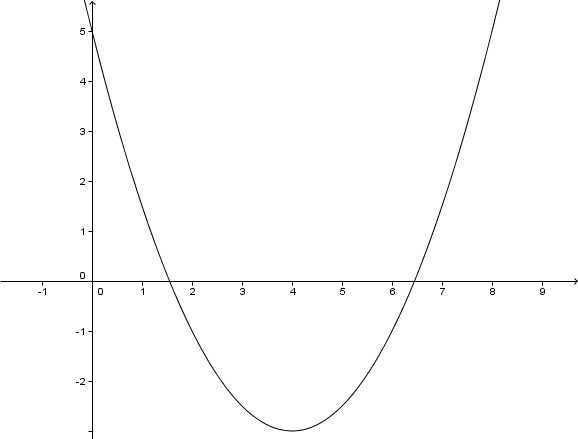
1.Scheitelpunkt berechnen
↓ ausklammern. Distributivgesetz.
↓ In die Scheitelform umwandeln. Dazu die quadratische Ergänzung machen.
↓ Umformen in eine Binomische Formel.
↓ Distributivgesetz anwenden.
2.Achsenschnittpunkte berechnen
Schnittpunkte mit der x-Achse
↓ Nullstelle berechnen . Die Gleichung gleich 0 setzen.
↓ Mitternachtsformel anwenden. Dazu zuerst die Diskriminante D berechnen.
↓ Hauptnenner bilden und auf diesen erweitern.
2 Lösungen
Mit Taschenrechner den genauen Wert berechenen.
Mit Taschenrechner den genauen Wert berechnen.
Schnittpunkt mit der y-Achse
↓ Für x gleich 0 setzen.
3.Verschiebung des Funktionsgraphen
Normalparabel:
Die verschiedenen Verschiebungen lassen sich an der Scheitelform ablesen.
Gestaucht mit .
Verschiebung um 1 LE nach rechts.
Verschiebung um LE nach unten.
4.Zeichnung
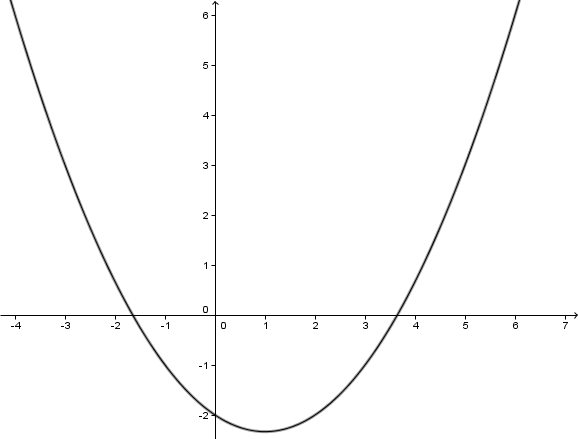
1.Scheitelpunkt berechnen
↓ ausklammern. Distributivgesetz.
↓ In die Scheitelform umwandeln. Dazu die quadratische Ergänzung machen.
↓ Umformen in eine Binomische Formel.
↓ Distributivgesetz anwenden.
2.Achsenschnittpunkte berechnen
Schnittpunkte mit der x-Achse
↓ Nullstelle berechnen . Die Gleichung gleich 0 setzen.
↓ Mitternachtsformel anwenden. Dazu zuerst die Diskriminante D berechnen.
↓ Hauptnenner bilden und auf diesen erweitern.
2 Lösungen
Mit Taschenrechner den genauen Wert berechnen.
Mit Taschenrechner den genauen Wert berechnen.
Schnittpunkt mit der y-Achse
↓ Für x gleich 0 setzen.
3.Verschiebung des Funktionsgraphen
Normalparabel:
Die verschiedenen Verschiebungen lassen sich an der Scheitelform ablesen.
Gestaucht mit .
Verschiebung um 1 LE nach rechts.
Verschiebung um LE nach unten.
4.Zeichnung

1.Scheitelpunkt berechnen
↓ ausklammern. Distributivgesetz.
↓ Kürzen mit 2.
↓ In die Scheitelform umwandeln. Dazu die quadratische Ergänzung machen.
↓ Gemeinsamen Hauptnenner bilden und auf diesen erweitern .
↓ Distributivgesetz anwenden.
↓ Kürzen der Faktoren mit 2.
↓ Kürzen der Faktoren mit 3.
2.Achsenschnittpunkte berechnen
Schnittpunkte mit der x-Achse
↓ Nullstelle berechnen . Die Gleichung gleich 0 setzen.
↓ Mitternachtsformel anwenden. Dazu zuerst die Diskriminante D berechnen.
↓ Gemeinsamen Hauptnenner bilden und auf diesen erweitern .
2 Lösungen
Mit Taschenrechner den genauen Wert berechnen.
Schnittpunkt mit der y-Achse
↓ x gleich 0 setzen.
3.Verschiebung des Funktionsgraphen
Normalparabel:
Die verschiedenen Verschiebungen lassen sich an der Scheitelform ablesen.
Nach unten geöffnet.
Gestaucht mit .
Verschiebung um LE nach rechts.
Verschiebung um LE nach oben.
4.Zeichnung