Computation Rules for Addition
The arithmetic laws for addition include the commutative law (law of interchange) and the associative law (law of brackets).
Commutative law (law of substitution)
According to the commutative law, it doesn't matter what order the ends of the sum are in, the result is always the same.
Example
Peter has two marbles and Kira has three. Together they have five.
But even if Peter has three marbles and Kira has two, together they have five marbles. It doesn't matter in which order the numbers 3 and 2 are added, the result is the same in both cases with 5.

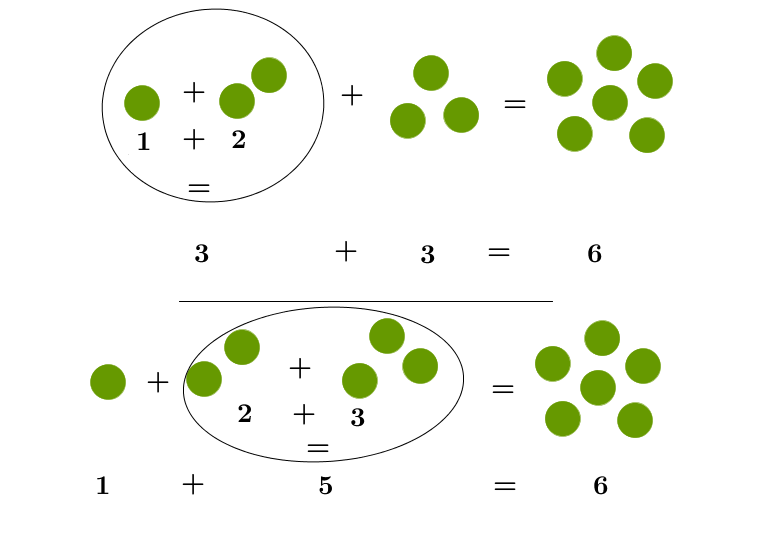
Associative law ("bracket resolving law")
When more than two addends are added, brackets help us know which parts are added together first.
Thus, with the addition
first the one and the two are added, and finally the three is added to their sum. So you get
With the addition
the two and the three are added first, and finally the one is added to their sum. Here we have
The associative law tells us that the sum remains unchanged no matter how the parentheses are placed.
Example
Peter has one marble, Kira has two and Michi has three. First Peter and Kira put their marbles together - that's three. Then Michi adds his. In total they have 6 marbles.
Kira and Michi can also put their marbles together first - that's five marbles. Later they also collect Peter's marble. Again, the three of them have a total of six marbles.
We can use these calculation rules to add as advantageously as possible. You can read how to do this in the article on calculation tricks.