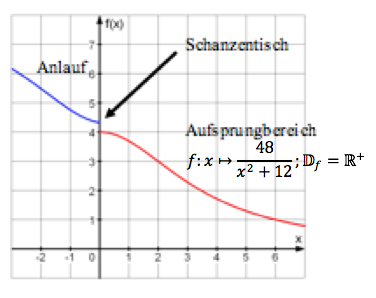
For this task you need the following basic knowledge: Kurvendiskussion
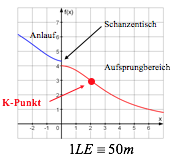
Aus physikalischen Gründen ist der K-Punkt die steilste Stelle der Aufsprungbahn. Mathematisch ist demnach der Wendepunkt der Funktion zu berechnen.
Bilde mithilfe der Quotientenrgel die Ableitung von :
Bilde mithilfe der Quotientenregel die 2. Ableitung:
Setze nun die 2. Ableitung Null und bestätige den Vorzeichenwechsel der 2. Ableitung an ihrer Nullstelle und damit das Vorliegen eines Wendepunktes.
Beachte, dass nur für positive definiert ist.
besitzt für einen Vorzeichenwechsel, da gilt:
Erstes Teilergebnis:
Der K-Punkt ist also horizontal vom Schanzentisch entfernt. (Dies ergibt eine "Großschanze".)
Berechne um den Neigungswinkel der Aufsprungbahn an der K-Linie zu erhalten.