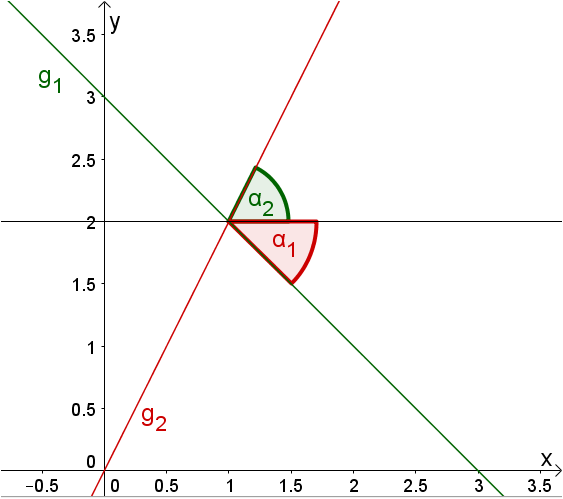
Exercises: Discussion of e-functions

Gegeben sind die Funktionen $f$ und $g$ mit $f (x) = 1 + e^{1 - x}$ und $g (x) = 2 \cdot e^{x - 1}$ .

Skizziere die beiden Graphen.
Bestimme den Schnittpunkt der beiden Graphen.
For this task you need the following basic knowledge: Schnittpunkten zweier Graphen
Du suchst nach Werten $x$ , die
in den Definitionsmengen $D_{f}$ und $D_{g}$ beider Funktionen $f$ und $g$ enthalten sind und
$f (x) = g (x)$ erfüllen.
Um solche Werte $x$ zu finden, löst du die Gleichung $f (x) = g (x)$ nach $x$ auf, falls dies möglich ist.
$f (x) = g (x)$
In diese Gleichung setzt du die Definitionsgleichungen $f (x) = 1 + e^{1 - x}$ und $g (x) = 2 e^{x - 1}$ von $f$ und $g$ ein.
$\Leftrightarrow 1 + e^{1 - x} = 2 e^{x - 1}$
Nun kannst du $x - 1$ durch $- (1 - x)$ ersetzen.
$\Leftrightarrow 1 + e^{1 - x} = 2 e^{- (1 - x)}$
Anschließend kannst du beide Seiten der Gleichung mit $e^{1 - x}$ multiplizieren, um die rechte Seite der Gleichung zu vereinfachen: Dabei ist aufgrund der Potenzgesetze $e^{1 - x} \cdot e^{- (1 - x)} = e^{0} = 1$ .
$\Leftrightarrow e^{1 - x} + (e^{1 - x})^{2} = 2$
Vertausche die Summanden (Kommutativgesetz der Addition).
$\Leftrightarrow (e^{1 - x})^{2} + e^{1 - x} = 2$
Dies erinnert an eine quadratische Gleichung. Nun kannst du mit $y = e^{1 - x}$ eine Substitution durchführen, d. h., du betrachtest eine veränderte Gleichung, in der du den komplizierteren Ausdruck $e^{1 - x}$ durch $y$ ersetzt; dies liefert eine einfacher aussehende Gleichung:
$y^{2} + y = 2$
Hier kannst du $2$ auf die linke Seite der Gleichung bringen.
$\Leftrightarrow y^{2} + y - 2 = 0$
Nun hast du eine quadratische Gleichung erhalten, die der Theorie gemäß höchstens zwei reelle Lösungen (d. h. Nullstellen) hat. Diese kannst du mit der $p q$ -Formel berechnen:
$\begin{aligned} y & = - \frac{1}{2} \pm \sqrt{{(\frac{1}{2})}^{2} - (- 2)} \\ = - \frac{1}{2} \pm \sqrt{\frac{1}{4} + 2} \\ = - \frac{1}{2} \pm \sqrt{\frac{9}{4}} \\ = - \frac{1}{2} \pm \frac{3}{2} \Leftrightarrow y \in {- 2, 1} \end{aligned}$
$\Leftrightarrow y \in {- 2, 1}$
(Hier gilt der Äquivalenzpfeil, da die Gleichung genau zwei reelle Lösungen hat.)
Die Exponentialfunktion $\exp : ℝ \to ℝ^{+}, x \mapsto e^{x}$ nimmt nur positive Werte an. Deswegen kann auch $e^{1 - x} = \exp (1 - x)$ nur positive Werte annehmen und die Gleichung $y = e^{1 - x}$ ist lediglich für $y = 1$ erfüllbar.
$e^{1 - x} = 1$
Wie du vielleicht schon weißt, ist $\exp (0) = e^{0} = 1$ . Also ist $x = 1$ eine mögliche Lösung. Durch Anwendung der natürlichen Logarithmusfunktion $\ln$ auf beide Seiten der Gleichung erhältst du
$\Leftrightarrow \ln (e^{1 - x}) = \ln (1)$
Da $\ln$ die Umkehrfunktion von $\exp$ auf ganz $ℝ$ ist (deswegen bleibt der Äquivalenzpfeil gültig), gilt $\ln (e^{x}) = x$ . Aus dem Artikel zur $\ln$ -Funktion könntest du dir gemerkt haben, dass $\ln (1) = 0$ ist.
$\Leftrightarrow 1 - x = 0$
Hier kannst du $x$ auf die andere Gleichungsseite bringen und bekommst die gesuchte Lösung der Gleichung $f (x) = g (x)$ .
$\Leftrightarrow x = 1$
Als Letztes musst du diesen $x$ -Wert noch in eine der beiden ursprünglichen Funktionen einsetzen, um den $y$ -Wert des Schnittpunkts herauszufinden.
$f (1) = 1 + e^{1 - 1} = 1 + e^{0} = 1 + 1 = 2$
Also liegt der gesuchte Schnittpunkt bei $S (1 | 2)$ .
Unter welchem Winkel schneiden sich die beiden Graphen?
For this task you need the following basic knowledge: Schnittpunkt zweier Geraden
Berechnung des Schnittwinkels zweier reeller Funktionen in einem Punkt:
Gegeben sind zwei Funktionen $f : D_{f} \to ℝ$ , $g : D_{g} \to ℝ$ , deren Graphen sich in einem Punkt $\tilde{x}$ gemäß Teilaufgabe b) schneiden: $f (\tilde{x}) = g (\tilde{x})$ . $f$ und $g$ wollen wir als in $\tilde{x}$ differenzierbar voraussetzen.
Du kannst nun folgendermaßen vorgehen: Berechne Geraden $g_{1} : y = k_{1} x + d_{1}$ und $g_{2} : y = k_{2} x + d_{2}$ , welche die nachstehenden Eigenschaften aufweisen:
$f^{'} (\tilde{x}) = k_{1}$ und $g^{'} (\tilde{x}) = k_{2}$
$f (\tilde{x}) = k_{1} \tilde{x} + d_{1}$ und $g (\tilde{x}) = k_{2} \tilde{x} + d_{2}$
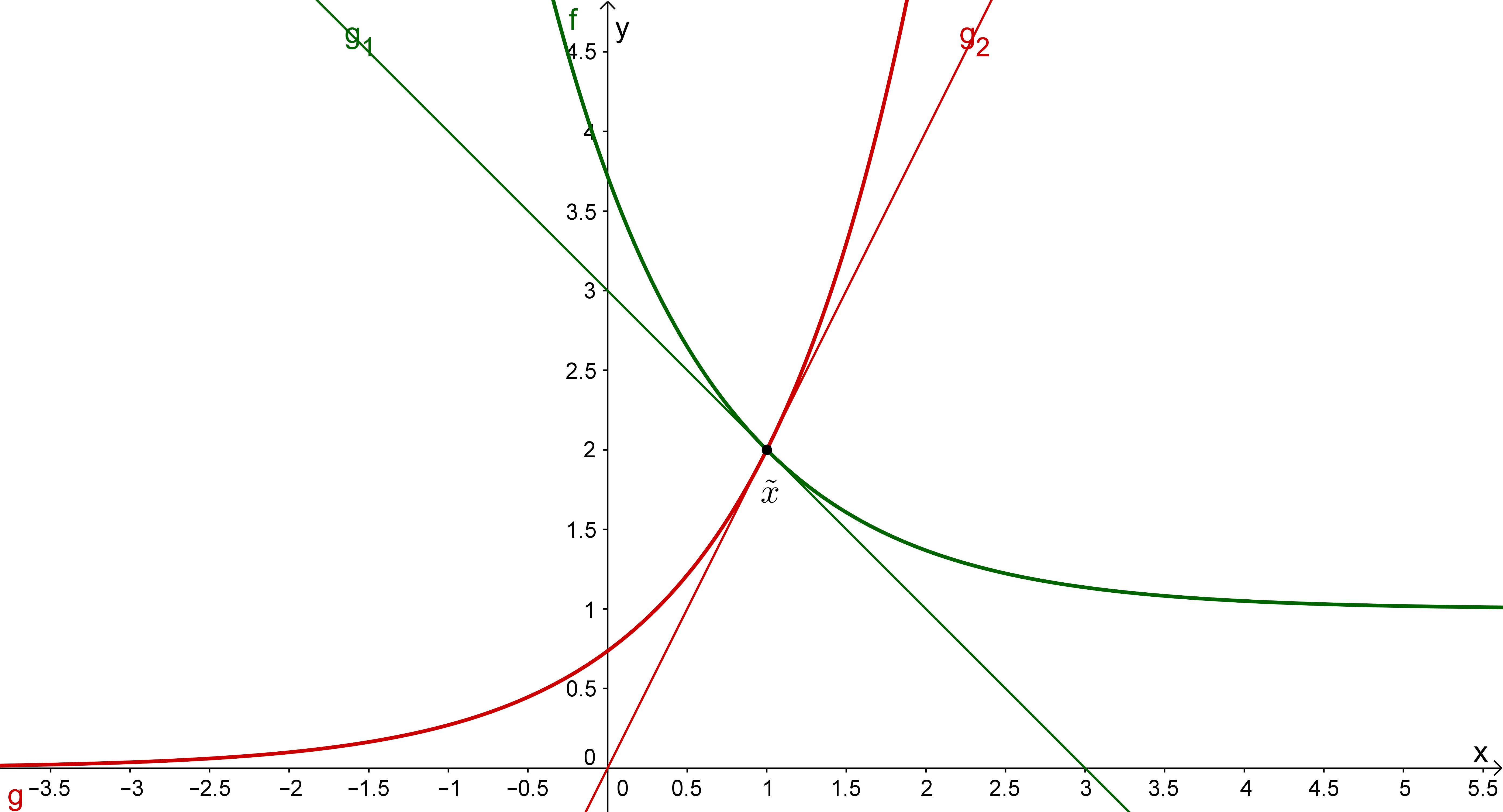
Dies bedeutet, in Worte gefasst:
Die Steigung von $g_{1}$ ist gleich der Steigung von $f$ in $\tilde{x}$ und die Steigung von $g_{2}$ ist gleich der Steigung von $g$ in $\tilde{x}$ .
Der Schnittpunkt $(\tilde{x}, f (\tilde{x})) = (\tilde{x}, g (\tilde{x}))$ der Graphen von $f$ und $g$ ist in $g_{1}$ und $g_{2}$ enthalten.
Anschließend kannst du den Schnittwinkel beider Geraden durch deren Richtungsvektoren $\vec{g_{1}}$ und $\vec{g_{2}}$ mittels der Formel $c o s (ϕ) = \frac{⟨ \vec{g_{1}}, \vec{g_{2}} ⟩}{| \vec{g_{1}} | \cdot | \vec{g_{2}} |}$ berechnen ( $⟨ ., . ⟩$ bezeichnet das Standardskalarprodukt):
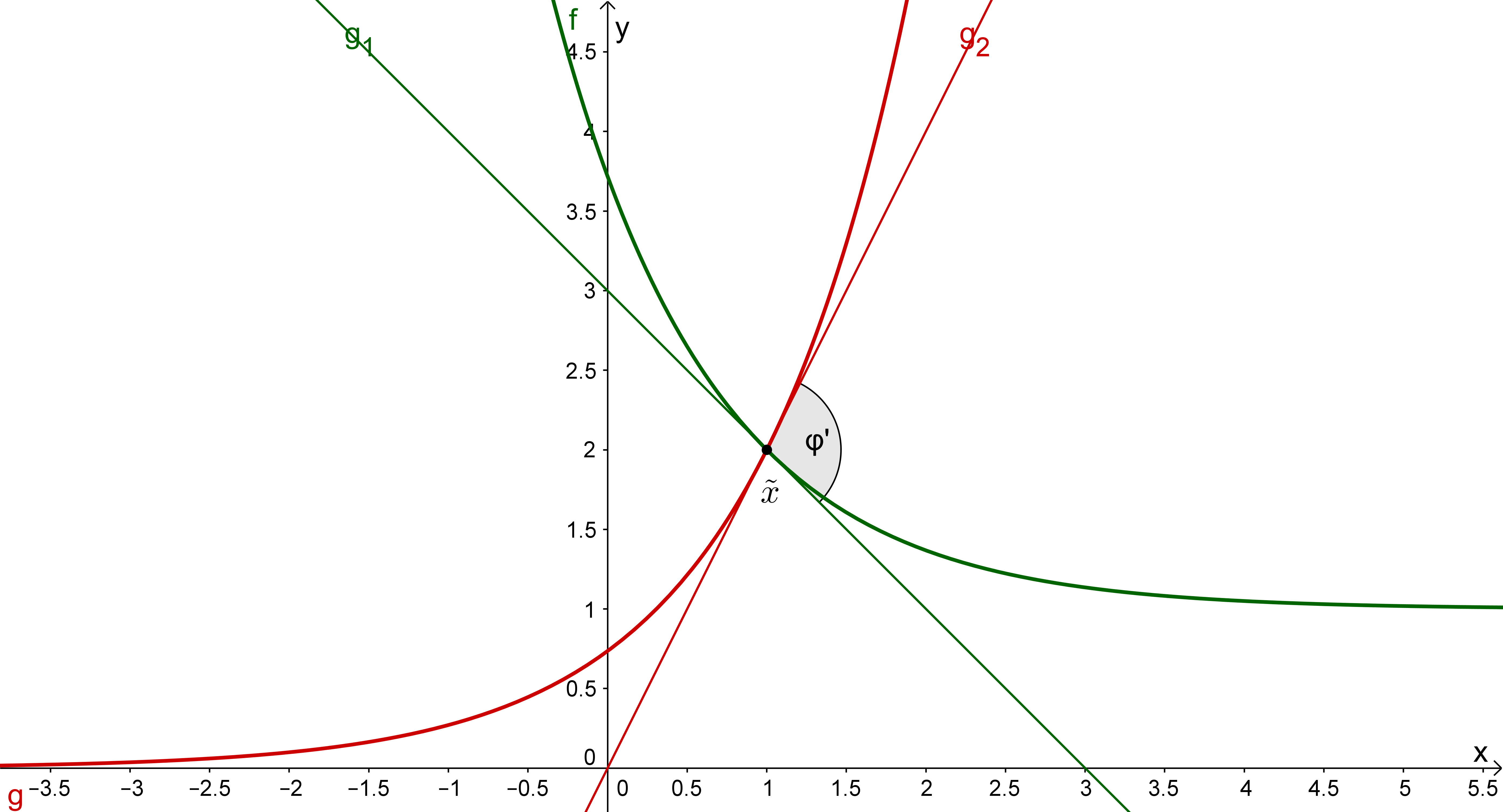
In Teilaufgabe b) war der Schnittpunkt $\tilde{x} = 1$ mit $f (1) = g (1) = 2$ .Um die Steigungen von $f$ und $g$ in $\tilde{x} = 1$ zu berechnen, benötigen wir deren Ableitungen an dieser Stelle:
$f^{'} (x) = - e^{1 - x}$ und $g^{'} (x) = 2 \cdot e^{x - 1}$ .
$f^{'} (1) = - e^{1 - 1} = - e^{0} = - 1$
$g^{'} (1) = 2 \cdot e^{1 - 1} = 2 \cdot e^{0} = 2$
Anschließend kannst du die gesuchten Geraden bestimmen, indem du $k_{1} = f^{'} (1)$ und $k_{2} = g^{'} (1)$ setzt (damit ist 1. erfüllt). Wenn du weiterhin noch 2. forderst, erhältst du durch Einsetzen von $\tilde{x} = 1, f (1), g (1), k_{1}$ und $k_{2}$ zwei Gleichungen. Diese Gleichungen formst du um, um die fehlenden Werte $d_{1}$ und $d_{2}$ zu berechnen:
$f (\tilde{x}) = k_{1} \tilde{x} + d_{1} \Leftrightarrow 2 = (- 1) \cdot 1 + d_{1} \Leftrightarrow d_{1} = 3$
und
$g (\tilde{x}) = k_{2} \tilde{x} + d_{2} \Leftrightarrow 2 = 2 \cdot 1 + d_{2} \Leftrightarrow d_{2} = 0$
Nach diesen Schritten hast du die Geradengleichungen von $g_{1}$ und $g_{2}$ ermittelt:
$g_{1} : y = (- 1) \cdot x + 3$
$g_{2} : y = 2 \cdot x$
(siehe auch: (*) Alternativer Lösungsweg)
Du kannst sofort die Normalform der Geraden angeben,
$g_{1} : x + y = 3$
$g_{2} : (- 2) \cdot x + y = 0$
sowie deren Normalenvektoren ${\vec{n}}_{g_{1}}$ und ${\vec{n}}_{g_{2}}$ ablesen: $(\binom{1}{1})$ und $(\binom{- 2}{1})$ .
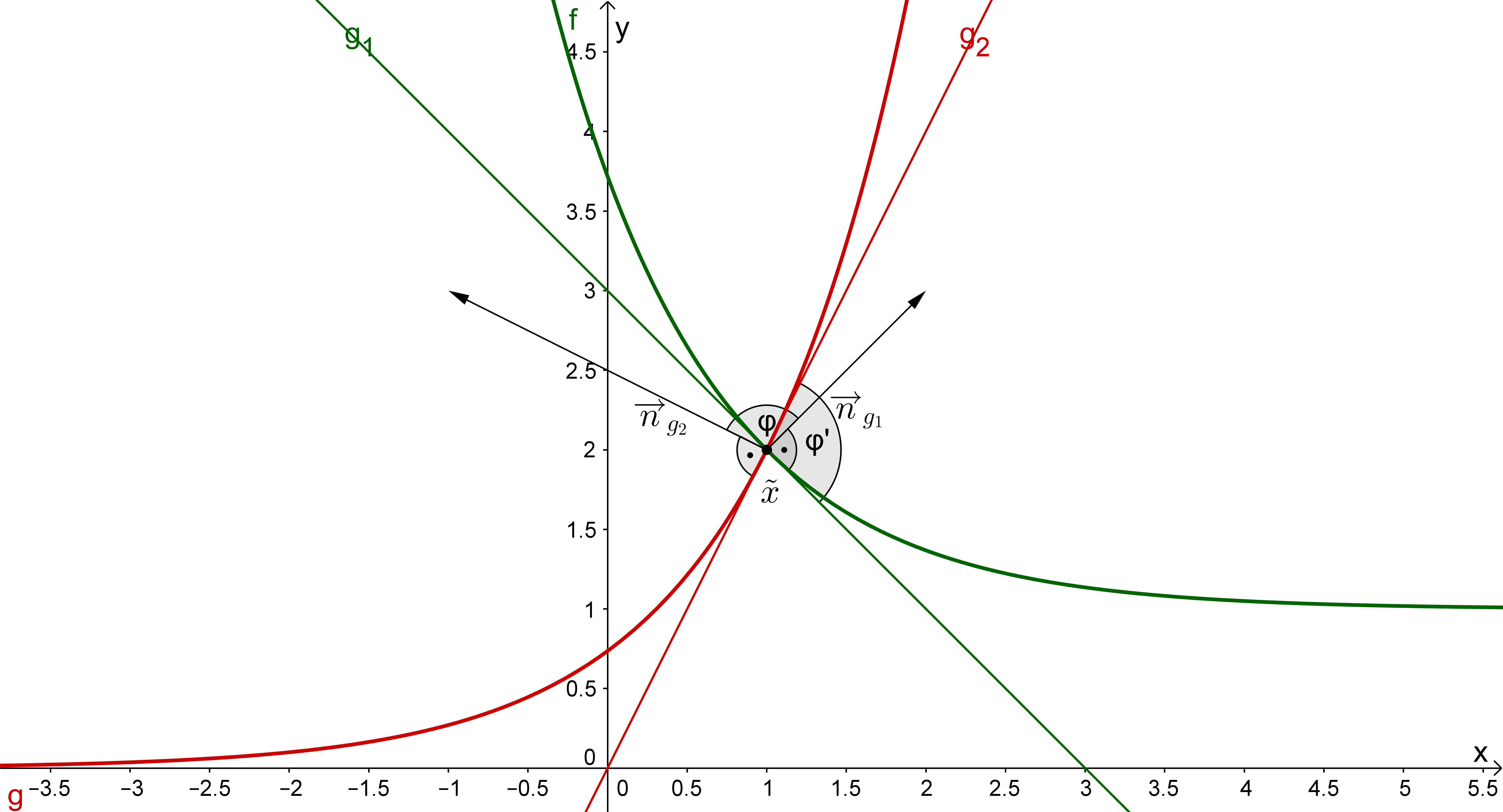
Da Normalenvektoren in der Ebene senkrecht, d.h. in einem Winkel von $90 °$ auf den Richtungsvektor der Geraden stehen, ist in obiger Grafik $φ = φ^{'}$ . Also kannst du $ϕ$ mit der weiter oben angegebenen Formel berechnen, wobei du jedoch nicht die Richtungs-, sondern die Normalenvektoren verwendest:
$\begin{aligned} c o s (φ) & = \frac{⟨ {\vec{n}}_{g_{1}}, {\vec{n}}_{g_{2}} ⟩}{| {\vec{n}}_{g_{1}} | \cdot | {\vec{n}}_{g_{2}} |} \\ = \frac{⟨ (\binom{1}{1}), (\binom{- 2}{1}) ⟩}{| (\binom{1}{1}) | \cdot | (\binom{- 2}{1}) |} \\ = \frac{- 2 + 1}{\sqrt{1 + 1} \cdot \sqrt{4 + 1}} \\ = - \frac{1}{\sqrt{2} \cdot \sqrt{5}} = - \frac{1}{\sqrt{10}} \end{aligned}$
$\begin{aligned} \Rightarrow φ & = c o s^{- 1} (- \frac{1}{\sqrt{10}}) \\ \approx 108,4 ° \end{aligned}$
Unter Verwendung eines Taschenrechners ist es dir möglich, den Wert von $c o s^{- 1} (- \frac{1}{\sqrt{10}})$ (in $°$ Winkelmaß) zu berechnen.
Achtung: Versichere dich davor in dessen Einstellungsmenü davon, dass du dein Ergebnis nicht in $°$ Radiant angegeben erhältst.
(*) Alternativer Lösungsweg
Dieser Lösungsweg verwendet keine Vektoren, sondern benutzt die Tatsache, dass die Steigung m einer Gerade durch $m = \tan (α)$ gegeben ist. Auflösen nach dem Steigungswinkel $α$ (=Winkel gegen die Horizontale) durch Anwenden von $\tan^{- 1} (. .)$ auf beiden Seiten der Gleichung liefert:
$α = \tan^{- 1} (m)$
Wir hatten:
$g_{1} : y = - x + 3$ mit Steigung $m_{1} = - 1$ .
$g_{2} : y = 2 \cdot x$ mit Steigung $m_{2} = 2$
Berechne nun den Steigungswinkel gemäß der Formel von oben.
Steigungswinkel von $g_{1}$ : $α_{1} = \tan^{- 1} (m_{1}) = \tan^{- 1} (- 1) = - 45^{\circ}$
Steigungswinkel von $g_{2}$ : $α_{2} = \tan^{- 1} (m_{2}) = \tan^{- 1} (2) \approx {63,4}^{\circ}$
Berechne den Schnittwinkel. Ziehe dazu die Winkel voneinander ab und bilde deren Betrag.
$φ = | α_{2} - α_{1} | \approx | {63,4}^{\circ} - (- 45^{\circ}) | = {108,4}^{\circ}$

This content is licensed under
CC BY-SA 4.0 → What does that mean? serlo.org

Exercises: Discussion of e-functions

Berechnung des Schnittwinkels zweier reeller Funktionen in einem Punkt:

(*) Alternativer Lösungsweg