Exercises: Derivative, symmetry and inverse of trigonometric functions

Der Graph der gesuchten Funktion ist achsensymmetrisch bezüglich der y-Achse.

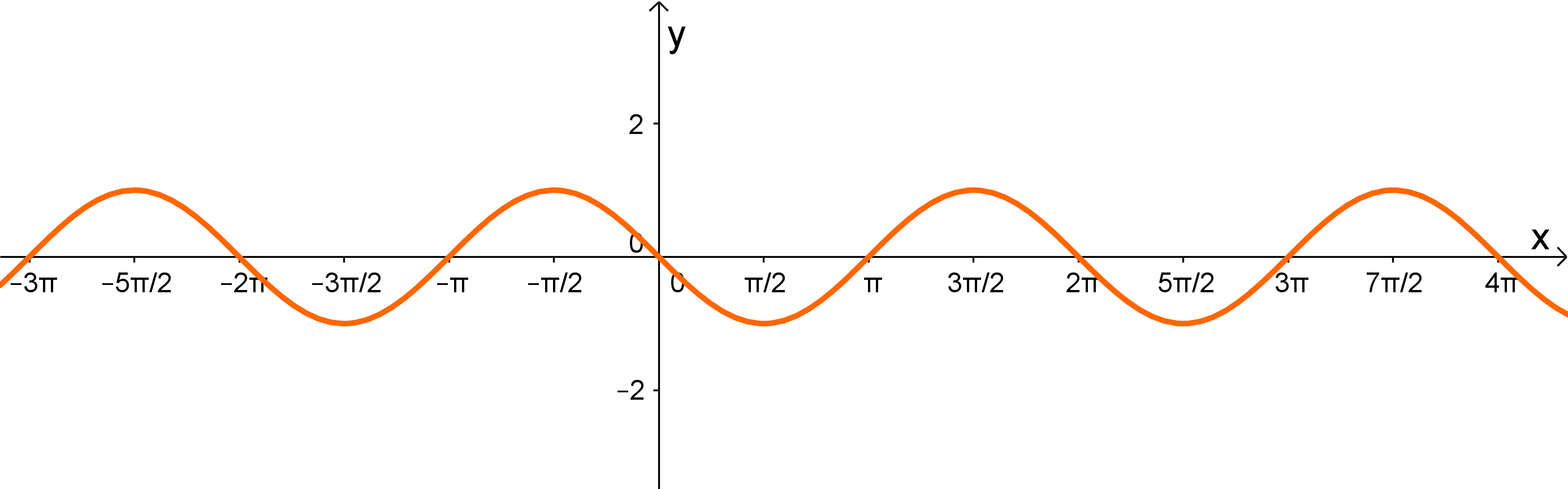
Somit kann man die beiden Funktionen $\cos (2\cdot x)$ und $\cos (2\cdot x)+3\cdot \pi$ ausschließen, denn $\cos (2\cdot x)$ ist die Standard Kosinus-Funktion bloß mit einer größeren Periode und $\cos (2\cdot x)+3\cdot \pi$ zusätzlich noch um $3\cdot \pi$ nach oben verschoben.

Bleiben also noch die beiden Sinus-Funktionen also Lösungsmöglichkeiten.

Die Funktion $\sin (x)$ ist punktsymmetrisch und im Intervall zwischen $0$ und $\pi$ positiv, die Funktion des gegeben Graphen ist punktsymmetrisch und im Intervall von $0$ bis $\pi$ negativ, also suchen wir eine Funktion die $\sin (x)$ um eine halbe Periode verschiebt.

Da die Periode der $sin(x)$ Funktion $2\cdot \pi$ lang ist, muss $\sin (x)$ um $\pi$ verschoben werden. Darum ist die richtige Lösung $\sin (x+\pi )$