Rational functions

A rational function is a function that can be represented as a fraction of polynomials.

That is, all rational functions are of the form $f (x) = \frac{p (x)}{q (x)}$ , where both $p (x)$ and $q (x)$ are polynomials.

According to the numerator and denominator degrees of the polynomials $p (x)$ and $q (x)$ one distinguishes between true rational functions and "false" rational functions.

Echt gebrochen-rationale Funktion

Der Grad des Zählerpolynoms $p (x)$ ist kleiner als der Grad des Nennerpolynoms $q (x)$ .

Beispiel

$\frac{4 x^{3} + 2 x^{2} - x}{2 x^{5}} \Rightarrow$ Grad von $p (x)$ ist $3$ , Grad von $q (x)$ ist $5$ .

Unecht gebrochen-rationale Funktion

Der Grad des Zählerpolynoms $p (x)$ ist größer oder gleich dem Grad des Nennerpolynoms $q (x)$ . Hier lässt sich die Funktion durch Polynomdivision in eine Funktion mit ganz-rationalem und echt gebrochen-rationalem Anteil zerlegen.

Beispiel

$\frac{6 x^{4} - x^{2} + 2 x}{5 x^{3}} \Rightarrow$ Grad von $p (x)$ ist $4$ , Grad von $q (x)$ ist $3$ .

Zerlegte Funktion: $\frac{6}{5} x - \frac{1}{5 x} + \frac{2}{5 x^{2}}$

Verschiedene Beispiele für gebrochen-rationale Funktionen

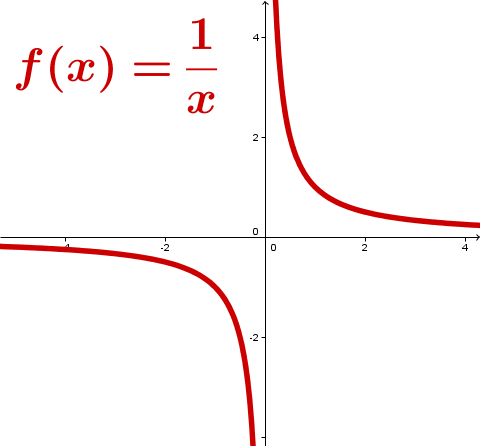
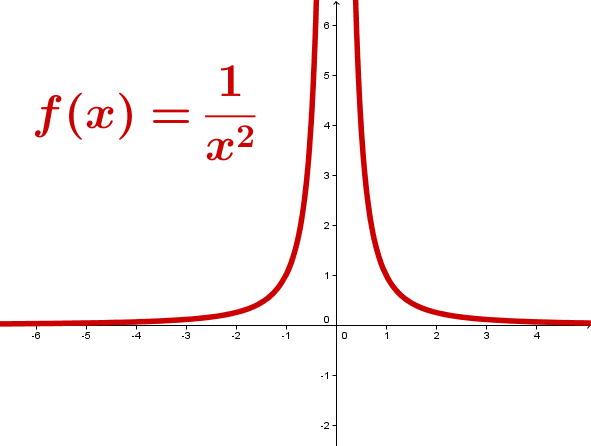
Echt gebrochen-rationale Funktionen

$f (x) = \frac{1}{x}$ (Hyperbel)

$f (x) = \frac{1}{x^{2}}$

Gebrochenrationale Funktion ohne Polstellen

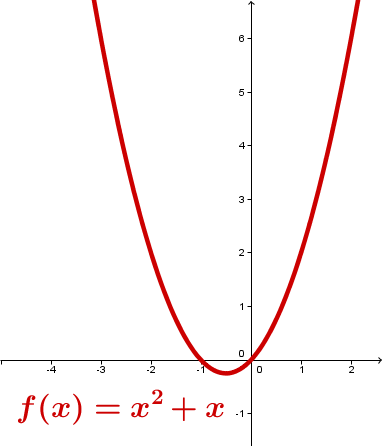
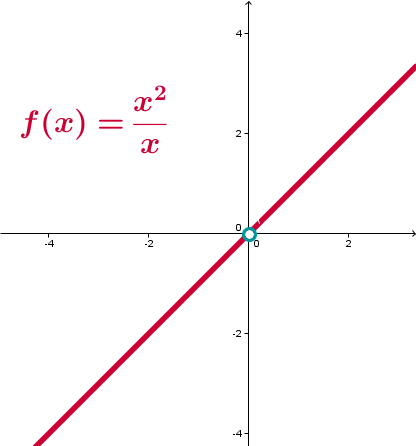
Unecht gebrochen-rationale Funktionen

Jedes Polynom, wie zum Beispiel: $f (x) = x^{2} + x (= \frac{x^{2} + x}{1})$

Quadratische Funktion Parabel nach oben geöffnet

$f (x) = \frac{x^{2}}{x}$

lineare Funktion ohne Null Defintionslücke

Beachte:

$\frac{x^{2}}{x} = f (x) \neq g (x) = x$ , denn $f$ und $g$ haben unterschiedliche Definitionsbereiche:

$D_{f} = ℝ ∖ {0}$
$D_{g} = ℝ$

Eigenschaften an Beispielen

Bei gebrochen-rationalen Funktionen lassen sich einige Eigenschaften, wie die Art und Lage der Asymptoten, an der Funktionsgleichung ablesen, sowohl an der ausmultiplizierten als auch an der faktorisierten Form.

Allgemeines Beispiel

$f (x)$	$=$	$\frac{{(x + 1)}^{2} \cdot {(x - 3)}^{3} \cdot (x + 2) \cdot x}{{(x + 1)}^{3} \cdot (x - 3) \cdot (x + 2) \cdot (x - 4) \cdot {(x + 5)}^{2}}$
	↓	Kürze $(x + 1)^{2}$ , $(x - 3)$ und $(x + 2)$ .
	$=$	$\frac{{(x - 3)}^{2} \cdot x}{(x + 1) \cdot (x - 4) \cdot {(x + 5)}^{2}}$

Aus dem Funktionsterm lässt sich nun ablesen:

$(x + 5)^{2}$ im Nenner: Asymptote durch die Polstelle ohne Vorzeichenwechsel bei $- 5$ (wegen geradem Exponenten $2$ )
$(x + 1)$ im Nenner: Asymptote durch die Polstelle mit Vorzeichenwechsel bei $- 1$ (wegen ungeradem Exponenten $1$ )
$(x - 4)$ im Nenner: Asymptote durch die Polstelle mit Vorzeichenwechsel bei $4$ (wegen ungeradem Exponenten $1$ )
$(x + 2)$ wurde gekürzt und kürzt sich weg: hebbare Definitionslücke bei $x = - 2$
$(x - 3)$ wurde gekürzt und bleibt im Zähler stehen: hebbare Definitionslücke mit der $x$ -Achse bei $x = 3$ (dadurch auch keine Nullstelle)
$x$ steht im Zähler: Nullstelle bei $x = 0$

gebrochenrationaler Funktionsgraph Definitionslücke Asymptote Polstelle

This content is licensed under
CC BY-SA 4.0 → What does that mean? serlo.org