A definition gap is a point of a function that lies outside the range.
We are in the case of a liftable definition gap, whenever the multiplicity of the zeros of the numerator are ≥ those of the denominator. You can then remove them by shortening.
(Stetig) hebbare oder behebbare Definitionslücken können bei gebrochen-rationalen Funktionen vorkommen.
Es gibt eine hebbare Definitionslücke bei , falls Nullstelle des Zählers und des Nenners ist und die Vielfachheit im Zähler größer ist als die im Nenner oder die Vielfachheiten gleich groß sind (die Nullstelle sich also aus dem Nenner kürzen lässt).
An dieser Stelle ist die Funktion nicht definiert, kann aber (stetig) fortgesetzt werden, deswegen bezeichnet man die Definitionslücke als hebbar.
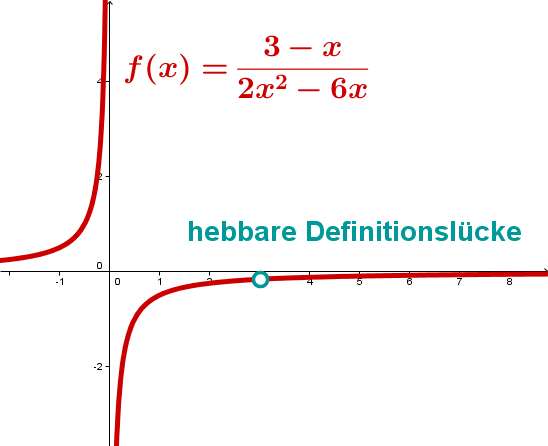
Graph der Funktion mit einer hebbaren Definitionslücke bei
Schließen der Lücke (Fortsetzen)
Man kann eine Funktion aus konstruieren, mit der man die Definitionslücke schließt:
Beispiel
hat eine hebbare Definitionslücke bei .
Man kürzt die Nullstelle aus dem Bruch, sodass sie im Nenner nicht mehr vorkommt.
Dann definiert man als den Wert, den man erhält, wenn man in den gekürzten Bruch einsetzt.
Man erhält , die Fortsetzung von f.
ist stetig.
Beispiel
Die Funktion hat den Definitionsbereich .
Setzt man 3 in die Funktion ein, ergibt sich .
Wenn man faktorisiert, sieht man, dass die Nullstelle aus dem Nenner gekürzt werden kann:
Es handelt sich bei 3 also um eine hebbare Definitionslücke.
Fortsetzung von f
wird aus dem Nenner gekürzt:
Man setzt 3 in den gekürzten Bruch ein:
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
