Sine and Cosine function
The sine and cosine functions are mathematical functions that can be used both
on the right-angled triangle, as well as
in circular geometry (trigonometry on the unit circle).
Due to the shape of their graphs, they also play an important role in the mathematical description of waves and oscillations.
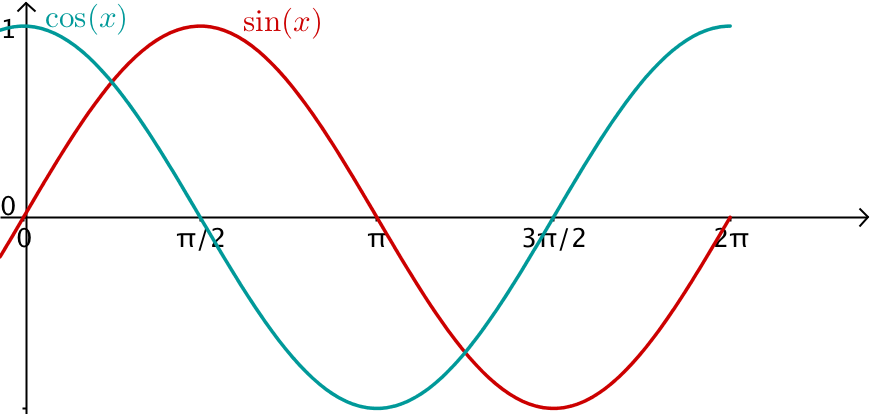
Eigenschaften
Der Sinus und der Kosinus haben beide
den gleichen Definitionsbereich (nämlich die reellen Zahlen)
den gleichen Wertebereich (das Intervall ) und sind beide
periodische Funktionen mit der Periode .
Außerdem ist der Sinus punktsymmetrisch zum Ursprung, und der Kosinus ist achsensymmetrisch zur y-Achse.
Sinus | Kosinus | |
|---|---|---|
Nullstellen | 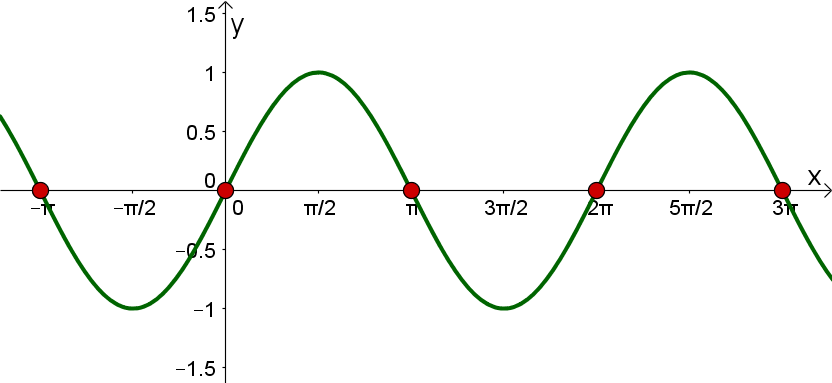 | 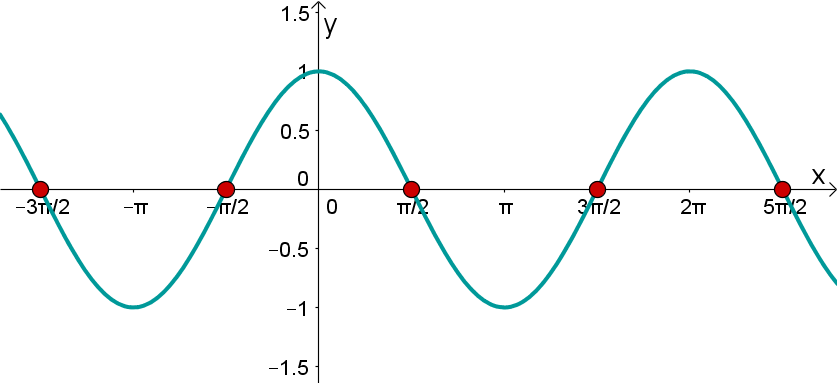 |
Man sieht an den Schnittpunkten mit der x-Achse, dass für jedes gilt: Das heißt sind die Nullstellen des Sinus. | Hier sieht man an den Schnittpunkten mit der x-Achse, dass für alle gilt: Das heißt sind die Nullstellen vom Kosinus. | |
Extrema (max. und min.) | 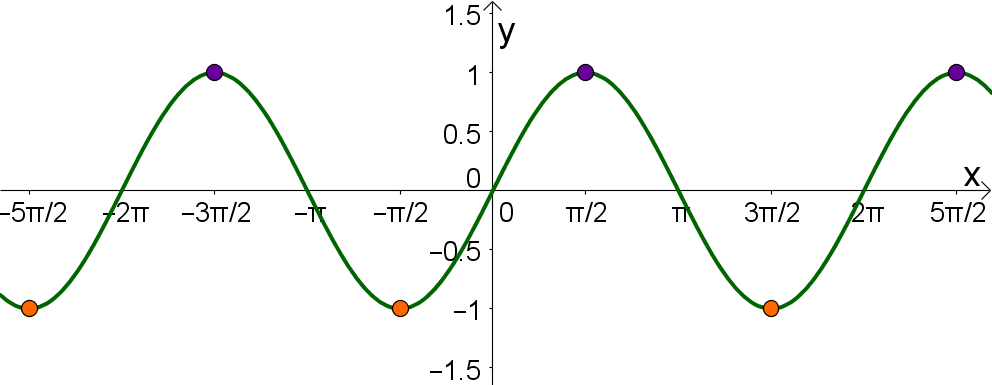 | 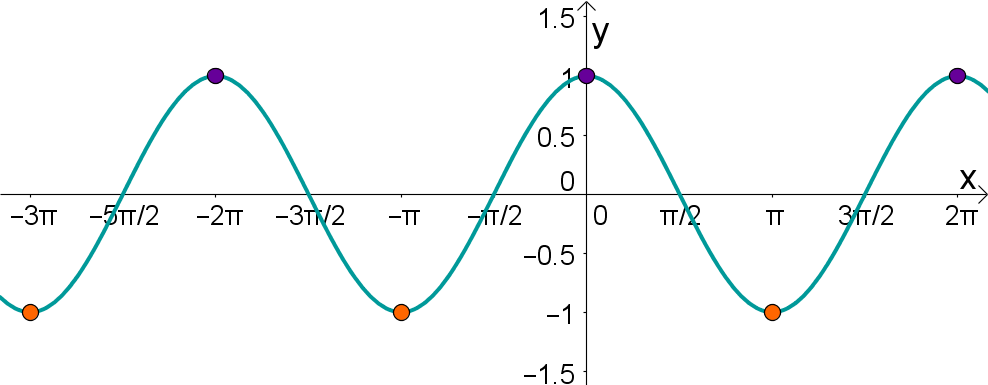 |
Extrema: Maximum | , das heißt sind die Maxima vom Sinus. | ℤ, das heißt sind die Maxima vom Kosinus. |
Extrema: Minimum | das heißt sind die Minima. | das heißt sind die Minima. |
Zusammenhang zw. sin(x) und cos(x) | Wenn man den Graphen der Sinusfunktion um nach links oder um nach rechts verschiebt, ist er deckungsgleich mit dem Graphen der Kosinusfunktion. Das heißt . | Wenn man den Graphen der Kosinusfunktion um nach links oder um nach rechts verschiebt, ist er deckungsgleich mit dem Graphen der Sinusfunktion. Das heißt . |
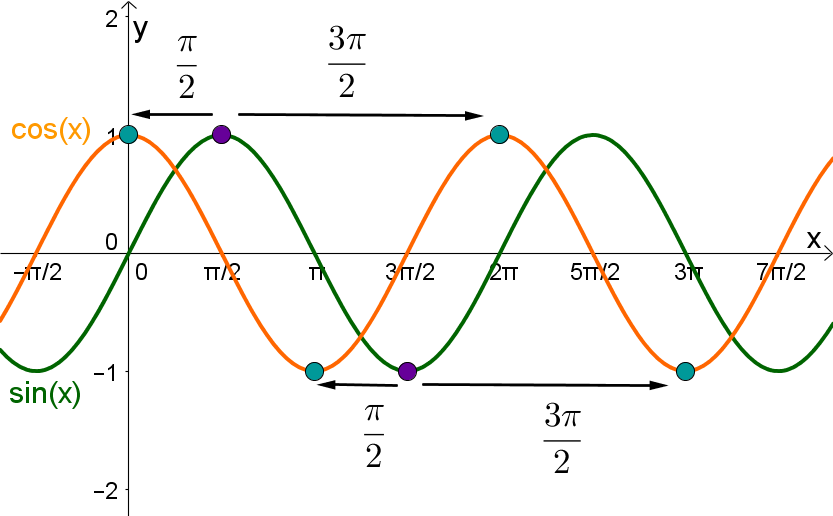 | 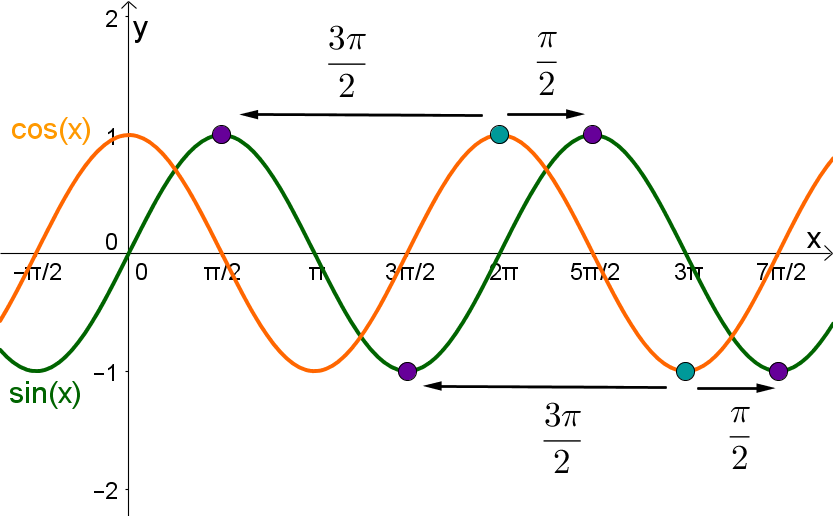 |
Beispielaufgaben
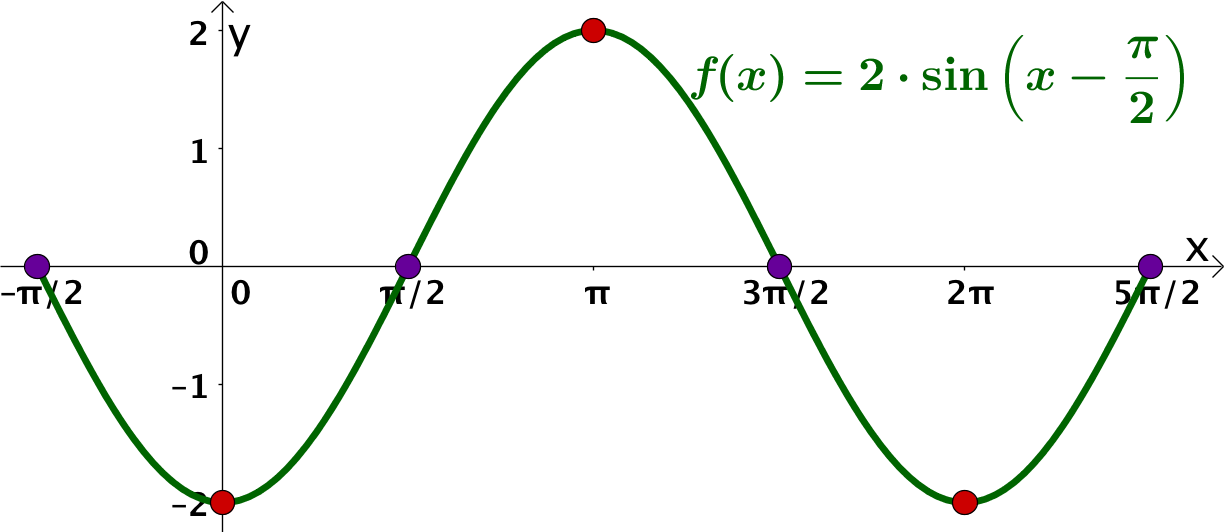
Skizziere die veränderte Sinusfunktion im Definitionsbereich in ein Koordinatensystem und lies ihren Wertebereich, Nullstellen und Extremstellen ab.
Tipp: Im Artikel Verschieben und Strecken von trigonometrischen Funktionen findet man, was die vor dem sin und das mit dem Graphen machen.
Lösung
Hier hast du eine Sinusfunktion mit Amplitude , welche um nach rechts verschoben wurde.
Lies das Gesuchte aus dem Graphen ab.
Wertebereich:
Nullstellen:
Extremstellen:
Video zu Sinus-, Kosinus-, und Tangensfunktion
Loading
Exercises
Loading
Loading
Loading
You can find more exercises in the following folder::
Gemischte Aufgaben zu trigonometrischen Funktionen
Still want more?
You can find more content on this topic here:
Articles
- Tangensfunktion
- Verschieben und Strecken von trigonometrischen Funktionen
- Beziehungen trigonometrischer Funktionen
- Zusammenhang zwischen Kreisbewegung und Sinus- und Kosinusfunktion
- Warum ist die Ableitung vom Sinus der Kosinus?