Exercises: Sine, Cosine and Tangent on a right triangle
Calculate the missing sides and angles of the isosceles triangle with . Note that we are looking at general isosceles triangles that are not necessarily right-angled.
a=44.2cm
c=63.4cm
For this task you need the following basic knowledge: Sine, Cosine and Tangent
Given: a=b= 44.2cm c=63.4cm
Required: h,
Draw a sketch for an overview.
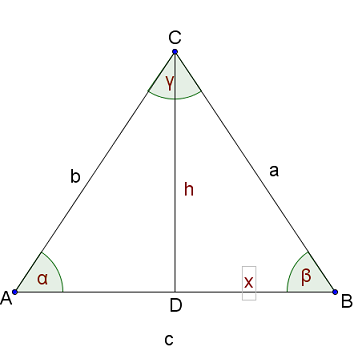
First compute .
Compute by using the Pythagorean theorem within the triangle .
↓ Plug in known values.
↓ square
↓ subtract
↓ take the root
Compute usig the sine.
↓ Plug in known values.
↓ Compute using a calculator.
↓ So we have a right triangle with
Since the base angles in an isosceles triangle are equal, and all interior angles total , you may calculate .
↓ multiply and subtract
Attention: The triangle is not a right triangle because no angle is .
a=114.5m
=32.3°
For this task you need the following basic knowledge: Sine, Cosine and Tangent
Given: =32.3°
Required: , ,
Draw a sketch for an overview.
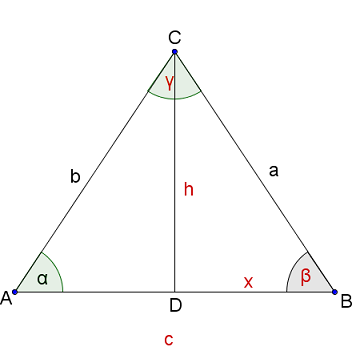
Since the base angles in an isosceles triangle are equal, and all interior angles total , you may calculate .
can be calculated using the sine.
↓ solve for and plug in values.
↓ multiply
is computed using the Pythagorean theorem within the triangle .
↓ Plug in known values.
↓ square
↓ subtract
↓ take the root
can be obtained by doubling the length of and then cutting the height of in half, such that equally long pieces are created.
c=35.4cm
=43.9°
For this task you need the following basic knowledge: Sine, Cosine and Tangent
Given: c=35.4cm =43.9°
Required: a, b, h, , x
Draw a sketch for an overview.

Since the base angles in an isosceles triangle are equal, and all interior angles total , you may calculate .
x is computed by cutting c into half.
a can be calculated using the cosine.
↓ Solve for and plug in values.
↓ h can be calculated using the tangent.
↓ Solve for and plug in values.
↓ multiply
h=14.8cm
28.3°
For this task you need the following basic knowledge: Sine, Cosine and Tangent
Given.: ;
Required.:
Draw a sketch for an overview.
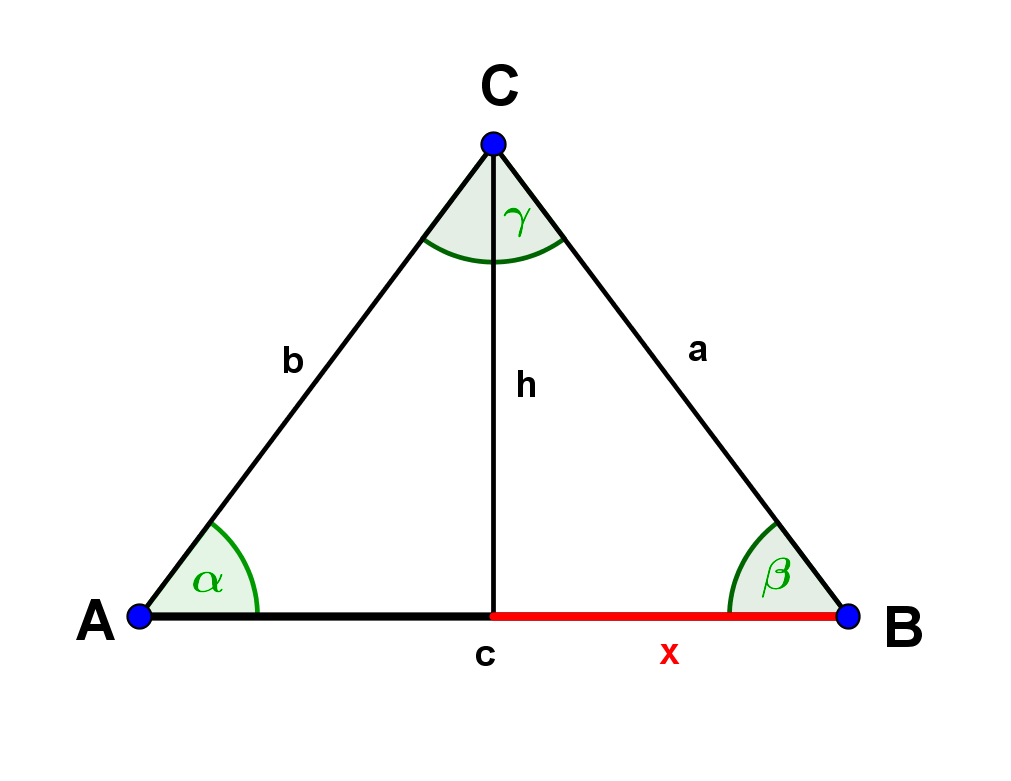
Since the base angles (here: and ) in an isosceles triangle are equal, and all the interior angles add up to (i.e. ), you can calculate directly with this information.
x can be calculated using the tangent.
↓ Solve for and plug in values.
↓ divide
↓ You get by doubling side .
can be calculated using the sine.
↓ Solve for and plug in values.
↓ divide
Since this is an isosceles triangle, the side length is just equal to the side length .
a=146.4m
h=58.4m
For this task you need the following basic knowledge: Sine, Cosine and Tangent
Given: ;
Required: , ,
Draw a sketch for an overview.
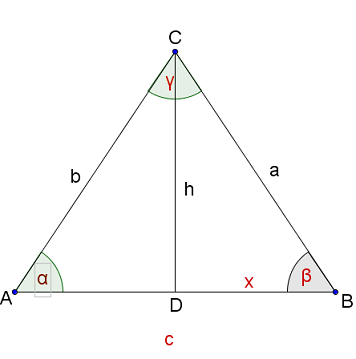
can be calculated using the sine.
↓ Plug in values and compute
Since the base angles in an isosceles triangle are equal, and all interior angles total , you may calculate .
can be calculated using the tangent.
↓ Solve for and plug in values.
↓ is computed by doubling side and then cutting the height of into half, such that equally long pieces result.