Exercises: Sine, Cosine and Tangent on a right triangle

1
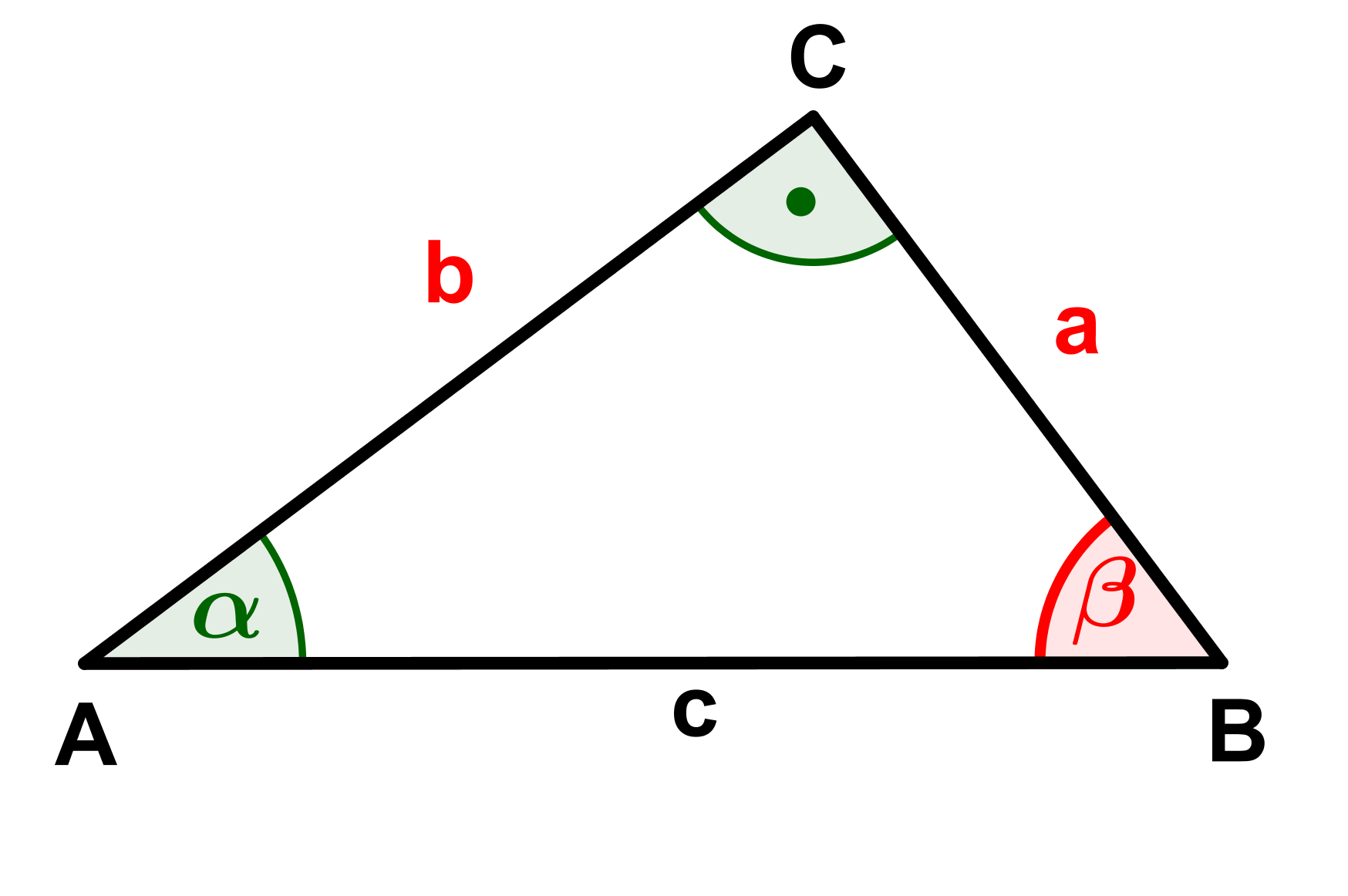
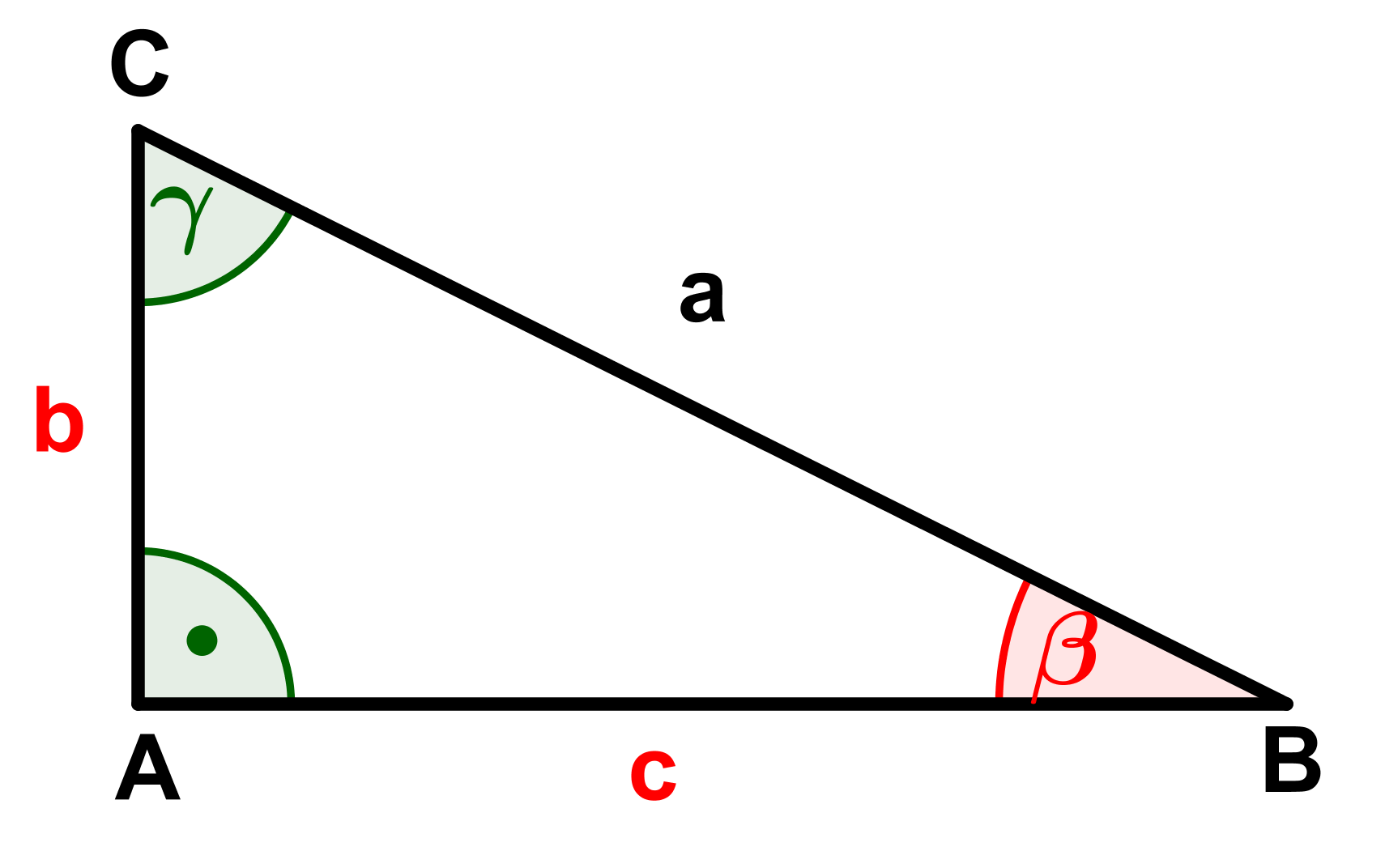
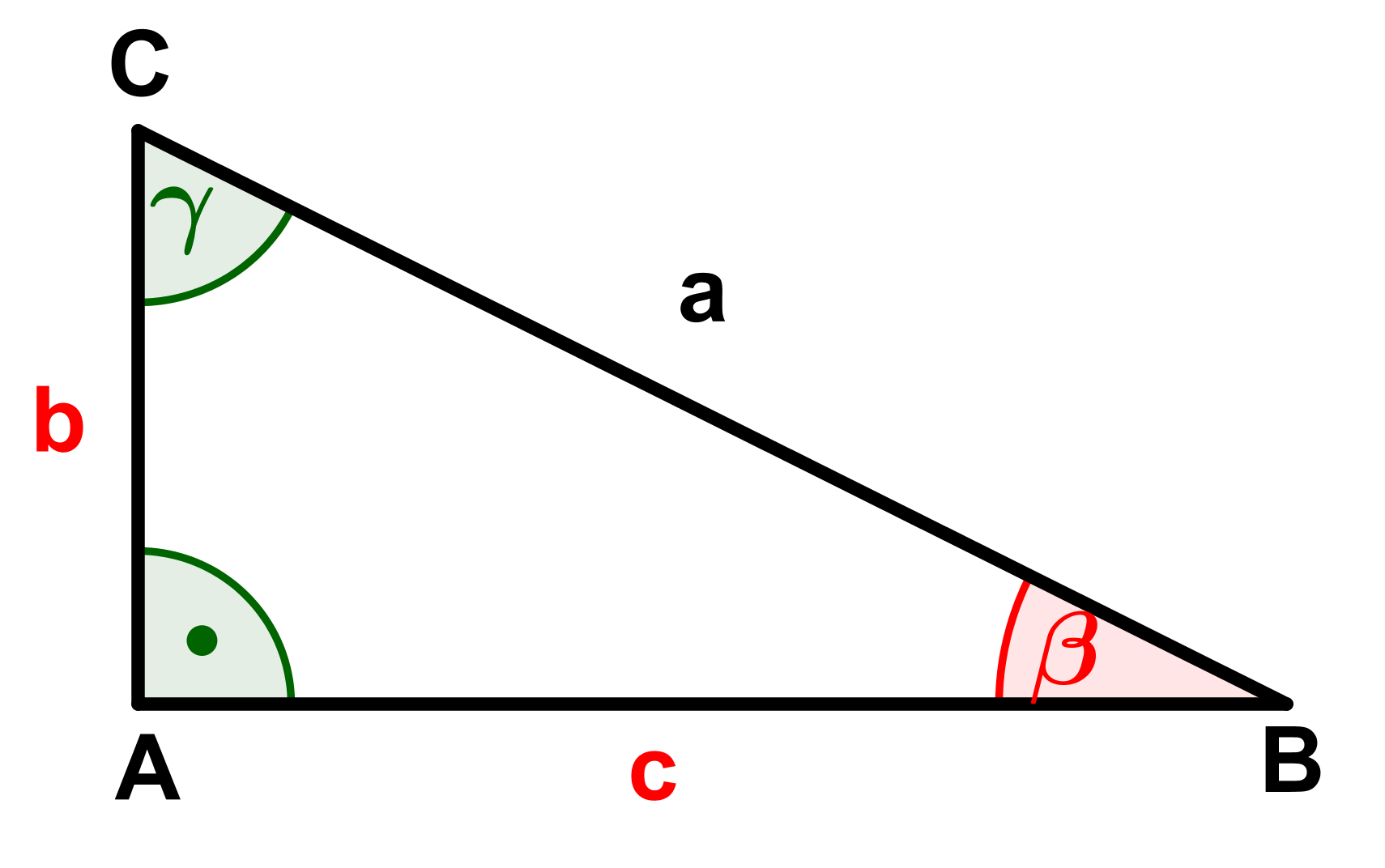
Calculate the missing sides and angles (marked red) of the triangles
$γ = 90^{\circ}$
$a = 12.7 cm$
$c = 24.9 cm$

For this task you need the following basic knowledge: Trigonometry on the unit circle
computing $α$
$\sin (α) = \frac{12.7 cm}{24.9 cm}$
$α = {30.7}^{\circ}$
computing $β$
You can calculate $β$ by subtracting all given angles from the total sum of all angles in a triangle $(180^{\circ})$ .
$β = 180^{\circ} - 90^{\circ} - {30.7}^{\circ}$
$β = {59.3}^{\circ}$
computing $b$
Then you compute $b$ using the Pythagorean theorem.
${(24.9 cm)}^{2} = {(12.7 cm)}^{2} + b^{2}$
$| - {(12.7 cm)}^{2}$
$b^{2} = {(24.9 cm)}^{2} - {(12.7 cm)}^{2}$
$b^{2} = 458.72 {cm}^{2}$
Take the root.
$b \approx 21.4 cm$

$α = 90^{\circ}$
$b = 420 m$
$a = 645 m$

For this task you need the following basic knowledge: Trigonometry on the unit circle
computing $β$
$\sin (β) = \frac{420 m}{645 m}$
$β = {40.6}^{\circ}$
computing $γ$
You can calculate $γ$ by subtracting all given angles from the total sum of all angles in a triangle $(180^{\circ})$ .
$γ = 180^{\circ} - 90^{\circ} - {40.6}^{\circ} = {49.4}^{\circ}$
computing $c$
Then you compute $c$ using the Pythagorean theorem.
Note in particular that c is not the hypotenuse of the triangle, but $a$ (see picture above), so that the Pythagorean form remains similar, but now $a$ , $b$ and $c$ do not take the familiar roles, where $a$ , $b$ would be the cathetuses and $c$ the hypotenuse.
$(645 m)^{2} = (420 m)^{2} + c^{2}$
$c^{2} = (645 m)^{2} - (420 m)^{2}$
$c^{2} = 239 625 m^{2}$
Take the root.
$c \approx 490 m$

$β = 90^{\circ}$
$c = 15.8 cm$
$a = 30.7 cm$

For this task you need the following basic knowledge: Trigonometry on the unit circle
computing $b$
Compute $b$ using the Pythagorean theorem.
$b^{2} = {(30.7 cm)}^{2} + {(15.8 cm)}^{2}$
$b^{2} = 1192.13 {cm}^{2} | \sqrt{}$
$b \approx 34.5 cm$
computing $α$
$\tan (α) = \frac{a}{c}$
$\tan (α) = \frac{30.7 cm}{15.8 cm}$
$α \approx {62.7}^{\circ}$
computing $γ$
You may calculate $γ$ by subtracting all given angles from the total sum of all angles in a triangle $(180^{\circ})$ .
$γ \approx 180^{\circ} - 90^{\circ} - {62.7}^{\circ}$
$γ \approx {27.3}^{\circ}$

$γ = 90^{\circ}$
$α = 35^{\circ}$
$c = 12.5 cm$

For this task you need the following basic knowledge: Trigonometry on the unit circle
computing $β$
You may calculate $β$ by subtracting all given angles from the total sum of all angles in a triangle $(180^{\circ})$ .
$β = 180^{\circ} - 90^{\circ} - 35^{\circ}$
$β = 55^{\circ}$
computing $a$
$\sin (35^{\circ}) = \frac{a}{12.5 cm} | \cdot 12.5 cm$
$a = \sin (35^{\circ}) \cdot 12.5 cm$
$a = 7.2 cm$
computing $b$
Then you compute $b$ using the Pythagorean theorem.
$c^{2} = a^{2} + b^{2}$
${(12.5 cm)}^{2} = {(7.2 cm)}^{2} + b^{2} | - {(7.2 cm)}^{2}$
$b^{2} = {(12.5 cm)}^{2} - {(7.2 cm)}^{2}$
$b^{2} \approx 104.4 {cm}^{2}$
Take the root.
$b \approx 10.2 cm$
computing $b$ (alternative solution with the cosine)
$\cos (α) = \frac{b}{c}$
Solve for $b$
$b = \cos (α) \cdot c \approx 10.2 cm$

$α = 90^{\circ}$
$γ = {40.3}^{\circ}$
$a = 10.5 cm$

For this task you need the following basic knowledge: Trigonometry on the unit circle
computing $β$
You may calculate $β$ by subtracting all given angles from the total sum of all angles in a triangle $(180^{\circ})$ .
$β = 180^{\circ} - 90^{\circ} - {40.3}^{\circ}$
$β = {49.7}^{\circ}$
computing $b$
$\sin ({49.7}^{\circ}) = \frac{b}{10.5 cm} | \cdot 10.5 cm$
$b = \sin ({49.7}^{\circ}) \cdot 10.5 cm$
$b \approx 8 cm$
computing $c$
Then you compute $c$ using the Pythagorean theorem.
${(10.5 cm)}^{2} = c^{2} + {(8 cm)}^{2}$
$c^{2} = 46.25 {cm}^{2}$
Take the root.
$c \approx 6.8 cm$
2
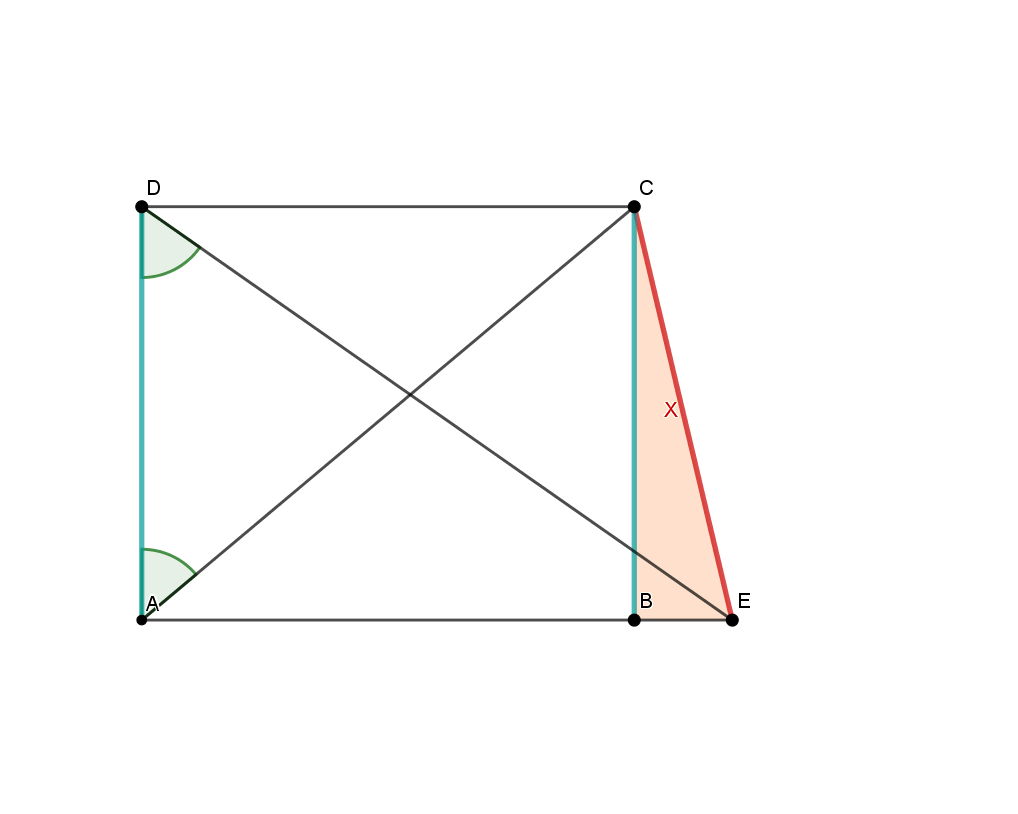
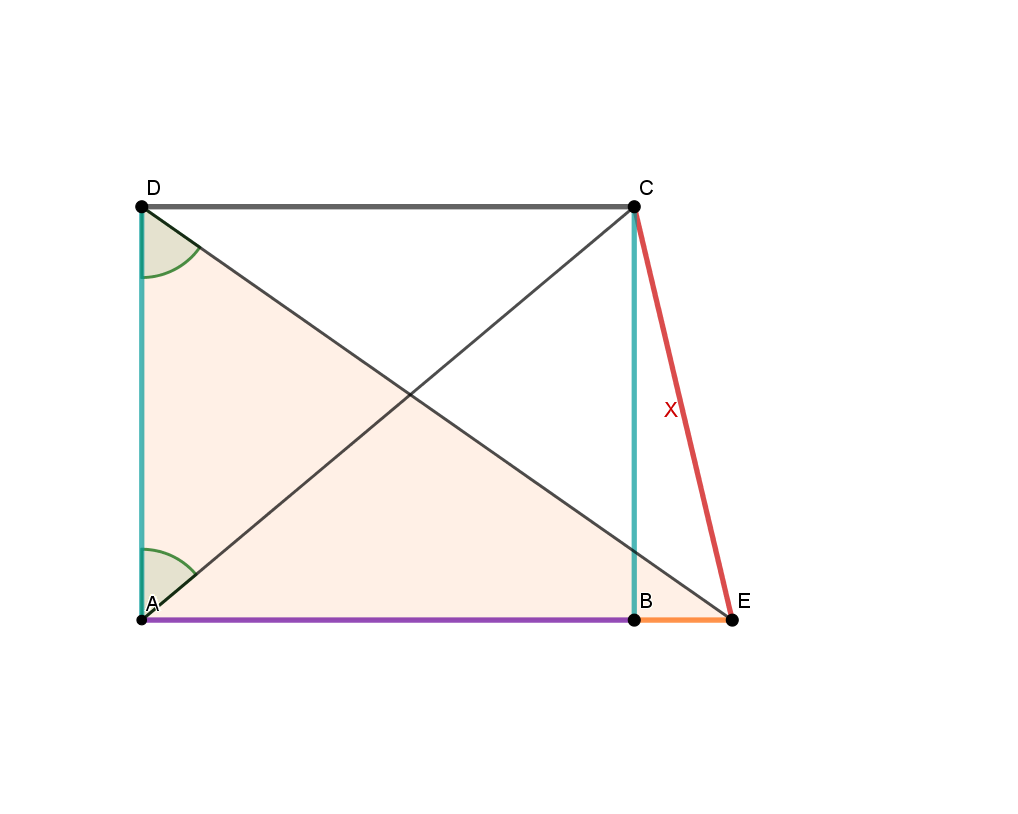
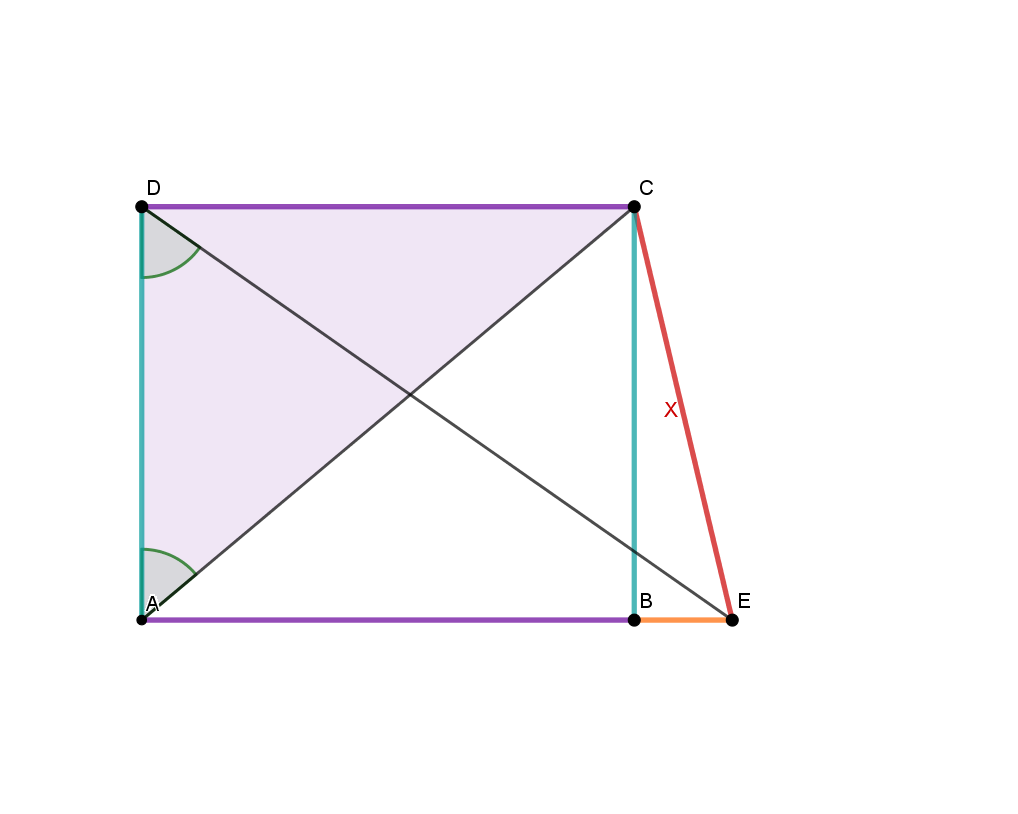
In a right triangle with $a = 5 cm$ and $α = 75 °$ compute the length of $b$ .

For this task you need the following basic knowledge: Sine, Cosine and Tangent
Given: $\begin{array}{l} a = 5 cm \\ α = 75 ° \end{array}$
Required: $b$
The opposite cathetus of $α$ is given and the adjacent cathetus of $α$ is sought. Therefore we use the tangent of $α$ .
$\tan (α)$ $=$ $\frac{a}{b}$ $\cdot b : \tan (α)$
↓
Solve for b
$b$ $=$ $\frac{a}{\tan (α)}$
↓
Plug in $a = 5 cm$ and $α = 75 °$
$b$ $=$ $\frac{5 cm}{\tan (75^{\circ})}$
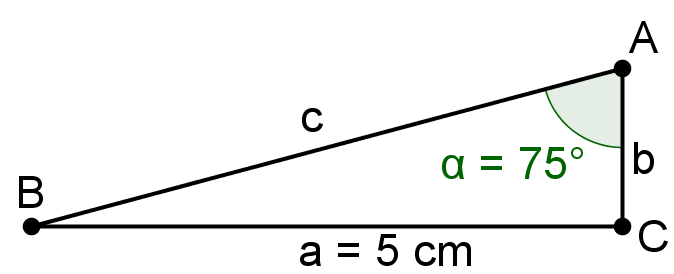
$b$ $=$ $1.34 cm$
Side $b$ has a length of approx. $1.34 cm$ .

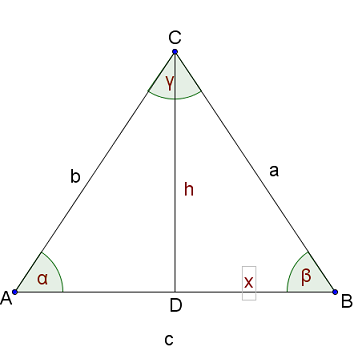
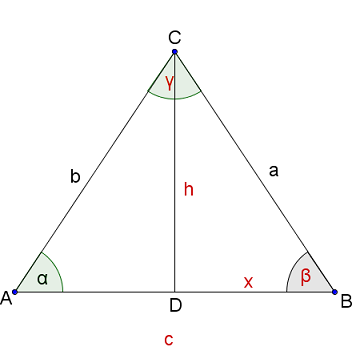
Calculate the missing sides and angles of the isosceles triangle $A B C$ with $a = b$ . Note that we are looking at general isosceles triangles that are not necessarily right-angled.

a=44.2cm
c=63.4cm

For this task you need the following basic knowledge: Sine, Cosine and Tangent
Given: a=b= 44.2cm c=63.4cm
Required: h, $α, β, γ$
Draw a sketch for an overview.
First compute $x$ .
$x$ $=$ $\frac{c}{2}$
$x$ $=$ $\frac{63.4 c m}{2}$
$=$ $31.7 c m$
Compute $h$ by using the Pythagorean theorem within the triangle $△ D B C$ .
$h$ $=$ $\sqrt{a^{2} - x^{2}}$
↓
Plug in known values.
$=$ $\sqrt{{(44.2 c m)}^{2} - {(31.7 c m)}^{2}}$
↓
square
$=$ $\sqrt{1953.64 c m^{2} - 1004.89 c m^{2}}$
↓
subtract
$=$ $\sqrt{948.75 c m^{2}}$
↓
take the root
$=$ $30.8 c m$
Compute $α$ usig the sine.
$\sin (α)$ $=$ $\frac{h}{b}$
↓
Plug in known values.
$=$ $\frac{30.8 c m}{44.2 c m}$
↓
Compute $α$ using a calculator.
$α$ $=$ $44.2 ° = β$
↓
So we have a right triangle with $α = β$
$=$
Since the base angles in an isosceles triangle are equal, and all interior angles total $180^{\circ}$ , you may calculate $γ$ .
$γ$ $=$ $180 ° - 2 \cdot 44.2 °$
↓
multiply and subtract
$=$ $91.6 °$
$\Rightarrow$ $h = 30.8 c m; α = β = {44.2}^{\circ}; γ = {91.6}^{\circ}$
Attention: The triangle $A B C$ is not a right triangle because no angle is $90 °$ .
a=114.5m
$α$ =32.3°

For this task you need the following basic knowledge: Sine, Cosine and Tangent
Given: $a = b = 114,5 m$ $α = β$ =32.3°
Required: $c$ , $h$ , $γ$
Draw a sketch for an overview.
Since the base angles in an isosceles triangle are equal, and all interior angles total $180^{\circ}$ , you may calculate $γ$ .
$γ$ $=$ $180 ° - 2 \cdot 32.3 °$
$=$ $115.4 °$
$h$ can be calculated using the sine.
$\sin (α)$ $=$ $\frac{h}{b}$
↓
solve for $h$ and plug in values.
$h$ $=$ $114.5 m \cdot \sin (32.3 °)$
↓
multiply
$=$ $61.2 m$
$x$ is computed using the Pythagorean theorem within the triangle $△ D B C$ .
$x$ $=$ $\sqrt{a^{2} - h^{2}}$
↓
Plug in known values.
$=$ $\sqrt{{(114.5 m)}^{2} - {(61.2 m)}^{2}}$
↓
square
$=$ $\sqrt{13110.25 m^{2} - 3745.44 m^{2}}$
↓
subtract
$=$ $\sqrt{9364.81 m^{2}}$
↓
take the root
$x$ $=$ $96.8 c m$
$c$ can be obtained by doubling the length of $x$ and then cutting the height $h$ of $c$ in half, such that $2$ equally long pieces $x$ are created.
$c = 2 \cdot 96.8 m = 193.6 m$
$\Rightarrow$ $h = 61.2 m; c = 193.6 m; γ = {115.4}^{\circ}$
c=35.4cm
$β$ =43.9°

For this task you need the following basic knowledge: Sine, Cosine and Tangent
Given: c=35.4cm $β = α$ =43.9°
Required: a, b, h, $γ$ , x
Draw a sketch for an overview.
Since the base angles in an isosceles triangle are equal, and all interior angles total $180^{\circ}$ , you may calculate $γ$ .
$γ$ $=$ $180 ° - 2 \cdot 43.9 °$
$=$ $92.2 °$
x is computed by cutting c into half.
$x$ $=$ $\frac{35.4 c m}{2}$
$=$ $17.7 c m$
a can be calculated using the cosine.
$\cos (β)$ $=$ $\frac{x}{a}$
↓
Solve for $a$ and plug in values.
$a$ $=$ $\frac{17.7 c m}{\cos (43.9 °)}$
↓
divide
$a$ $=$ $24.6 c m$
h can be calculated using the tangent.
$\tan (β)$ $=$ $\frac{h}{x}$
↓
Solve for $h$ and plug in values.
$h$ $=$ $17.7 c m \cdot \tan (43.9 °)$
↓
multiply
$h$ $=$ $17.0 c m$
$\Rightarrow$ $α = {43.9}^{\circ}; γ = {92.2}^{\circ}; a = b = 24.6 c m; h = 17.0 c m$
h=14.8cm
$α = β =$ 28.3°

For this task you need the following basic knowledge: Sine, Cosine and Tangent
Given.: $h = 14.8 c m$ ; $α = β = {28.3}^{\circ}$
Required.: $β, γ, c, b, a$
Draw a sketch for an overview.
Since the base angles (here: $α$ and $β$ ) in an isosceles triangle are equal, and all the interior angles add up to $180^{\circ}$ (i.e. $α + β + γ = 180^{\circ}$ ), you can calculate $γ$ directly with this information.
$γ$ $=$ $180 ° - 2 \cdot 28.3 °$
$=$ $123.4 °$
x can be calculated using the tangent.
$\tan (β)$ $=$ $\frac{h}{x}$
↓
Solve for $x$ and plug in values.
$x$ $=$ $\frac{14.8 c m}{\tan (28.3 °)}$
↓
divide
$x$ $=$ $27.5 c m$
↓
You get $c$ by doubling side $x$ .
$c$ $=$ $2 \cdot 27.5 c m$
$=$ $55 c m$
$b$ can be calculated using the sine.
$\sin (α)$ $=$ $\frac{h}{b}$
↓
Solve for $b$ and plug in values.
$b$ $=$ $\frac{14.8 c m}{\sin (28.3 °)}$
↓
divide
$=$ $31.2 c m$
Since this is an isosceles triangle, the side length $a$ is just equal to the side length $b$ .
$\Rightarrow$ $γ = {123.4}^{\circ}; c = 55 c m; a = b = 31.2 c m$

a=146.4m

h=58.4m

4
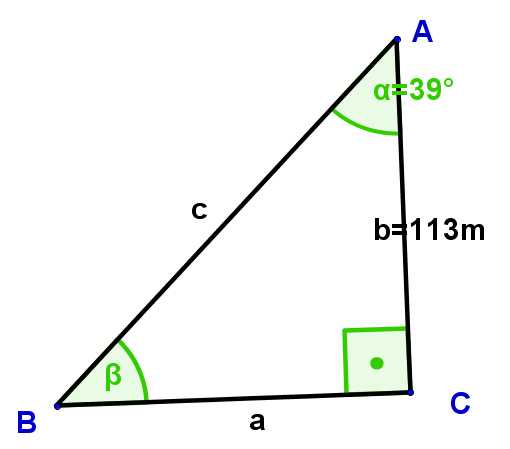
A triangle with a right angle at $C$ , with side $b = 113 m$ has an angle $α = 39^{\circ}$ . First make a sketch and then calculate all the missing sides and the other angle $β$ .

For this task you need the following basic knowledge: Sine, Cosine and Tangent
1. Make a sketch
2. Calculate
$\cos (39 °)$ $=$ $\frac{113 m}{c}$ $\cdot c$
↓
Get c on one side
$c \cdot \cos (39 °)$ $=$ $113 m$ $: \cos (39 °)$
$c$ $=$ $\frac{113 m}{\cos (39 °)}$
$c$ $=$ $145 m$
Calculate $β$ by subtracting all given angles from the total sum of all angles in a triangle $(180^{\circ})$ .
$β + 90 ° + 39 °$ $=$ $180 °$
$β$ $=$ $180 ° - 90 ° - 39 °$
$β$ $=$ $51 °$
$\sin (39 °)$ $=$ $\frac{a}{145 m}$ $\cdot 145 m$
$a$ $=$ $\sin (39 °) \cdot 145 m$
$a$ $=$ $91 m$
5
Sketch a rectangle with sides $a = 7 c m$ and $b = 18 c m$ and calculate the angles
between a diagonal and the sides

For this task you need the following basic knowledge: Sine, Cosine and Tangent
Given: $a = 7 cm$ ; $b = 18 cm$
Required: $α, β,$
You may start by drawing a sketch.
Compute $α$ using the tangent.
$\tan (α) = \frac{a}{b}$
Insert the values and calculate $α$ using the calculator.
$\tan (α) = \frac{7 cm}{18 cm}$
$α = {21.3}^{\circ}$
Compute $β$ . $α$ and $β$ add up to 90° , so for $β$ , we have:
$β = 90^{\circ} - {21,3}^{\circ} = {68.7}^{\circ}$
$\Rightarrow$ The angle $α$ is 21.3°. $β$ equals 68.7°.

between both diagonals

For this task you need the following basic knowledge: Sine, Cosine and Tangent
Given: $α = {68.7}^{\circ}; β = {21.3}^{\circ}$
Required: $γ, δ$
You may start by drawing a sketch.
$δ$ equals 2 $α$ , since $δ$ $+$ $γ$ $=$ 180° and $γ$ $+ 2$ $α$ $=$ 180° holds in a right triangle.
$\Rightarrow$ $δ$ + $γ$ $=$ $γ$ $+ 2$ $α$
$\Rightarrow$ $δ$ $=$ $2$ $α$
$δ = 2 \cdot {68.7}^{\circ} = {137.4}^{\circ}$
$γ$ and $δ$ add up to 180°.
$γ = 180^{\circ} - {137.4}^{\circ} = {42.6}^{\circ}$
$\Rightarrow$ The angle $γ$ equals 42,6°. $δ$ amounts to 137.4°.
6
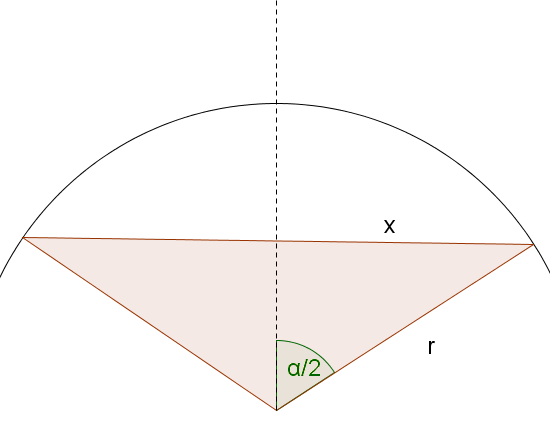
In a circle with radius $r = 10 c m$ the chord $s$ has the central angle $α = 84^{\circ}$ .
What is the length of the chord?

For this task you need the following basic knowledge: Sine, Cosine and Tangent
Given.: $r = 10 c m$ ; $α = 84^{\circ}$
Required.: $x$
First, draw a sketch.
Compute $x$ using the sine.
$\sin (\frac{α}{2})$ $=$ $\frac{x}{r}$
↓
Solve for $x$ and plug in values.
$x$ $=$ $10 c m \cdot \sin (\frac{84^{\circ}}{2})$
↓
Compute $x$ .
$x$ $=$ $6.7 c m$
↓
Since $x$ is half of the chord $s$ , double it to get the chord $s$ .
$s$ $=$ $2 \cdot 6.7 c m$
$s$ $=$ $13.4 c m$
$\Rightarrow$ The length of the chord is $13.4 c m$ .
7
Heike is $1.69 m$ tall. How long is her shadow when the sun's rays hit the ground at an angle of $30 °$ ? Give the result in metres rounded to 2 decimal places.
m
8
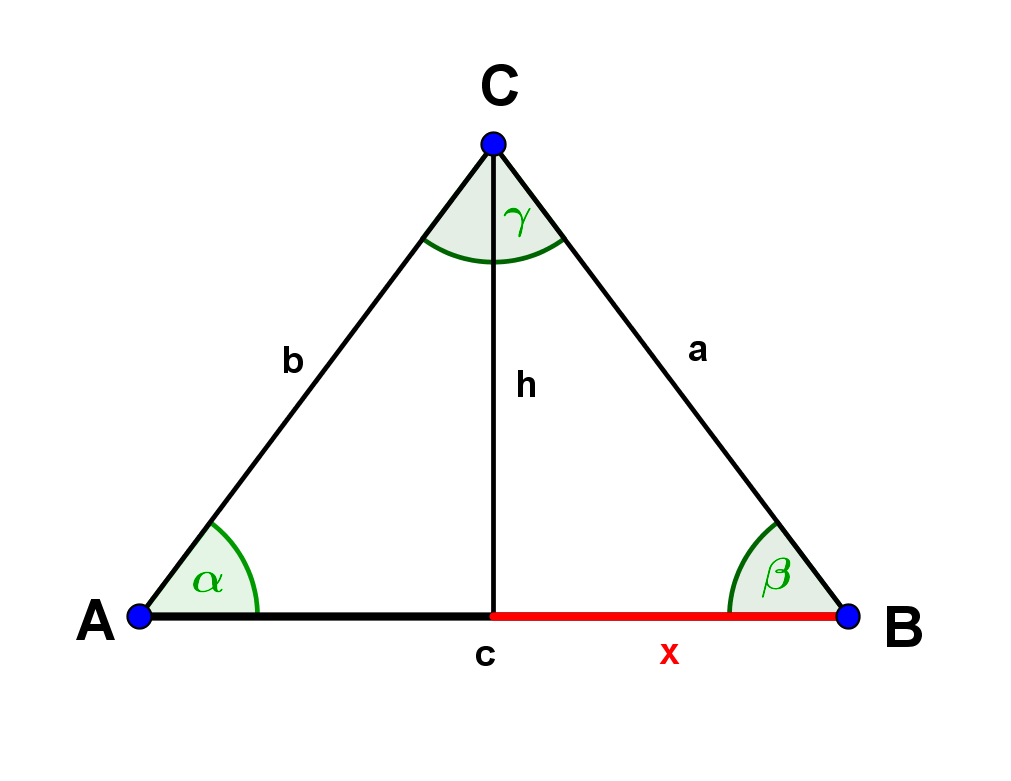
Calculate the missing sides and angles of the isosceles triangle $A B C$ with $a = b$ .
a = 44.2cm
c = 63.4cm

Calculate the height of the triangle.
Apply the Pythagorean theorem to calculate the height.
$h_{c} = \sqrt{b^{2} - {(\frac{1}{2} c)}^{2}} \approx 30.802 c m$
Now calculate $α$ , $β$ and $γ$ using sine or cosine.
$\sin (α)$ $=$ $\frac{h_{c}}{b}$
$α$ $\approx$ $44,177 ° .$
or:
$\cos (α)$ $=$ $\frac{\frac{1}{2} c}{b}$
$α$ $=$ $44.177 °$
$\sin (β)$ $=$ $\frac{h_{c}}{α}$
$β$ $\approx$ $44.177 °$
$\cos (β)$ $=$ $\frac{\frac{1}{2} c}{a}$
$β$ $=$ $44.177 °$
Add the two angles and subtract them from the sum of the angles in the triangle.
$γ$ $=$ $180 ° - 2 \cdot 44.177 ° .$
$γ$ $=$ $91.646 °$
alternatively:
$\cos (\frac{1}{2} γ)$ $=$ $\frac{\frac{1}{2} c}{a}$
$\frac{1}{2} γ$ $\approx$ ${45.8}^{°}$
$γ$ $\approx$ ${45.8}^{\circ} \cdot 2 = {91.6}^{\circ}$
or:
$\sin (\frac{1}{2} γ)$ $=$ $\frac{h_{c}}{a}$
$\frac{1}{2} γ$ $=$ $45.8 °$
$γ$ $=$ $2 \cdot 45.8 ° = 91.6 °$

a = 114.5m
$α$ = 32.3°

For this task you need the following basic knowledge: Triangle
Calculate the side $c$ of the triangle:
Use the cosine to calculate the base of the triangle,
$\cos (α)$ $=$ $\frac{\frac{1}{2} c}{b}$ $\cdot b$
$\cos (32.3 °) \cdot 114.5 m$ $=$ $\frac{1}{2} c$ $\cdot 2$
$2 \cdot (\cos (32.3 °) \cdot 114.5 m)$ $=$ $c$
$c$ $=$ $193.565$
Calculate the height of the triangle:
You may use the sine to do this.
$\sin (α)$ $=$ $\frac{h_{c}}{b}$ $\cdot b$
$\sin (32.3 °) \cdot 114.5 m$ $=$ $h_{c}$
$h_{c}$ $=$ $61.183 m$
↓
Calculate the two missing angles using sine or cosine
$=$
$\cos (β)$ $=$ $\frac{\frac{1}{2} c}{a}$
$β$ $=$ $32.3 °$
$\sin (β)$ $=$ $\frac{h}{a}$
$β$ $=$ $32.3 °$
$γ$ $=$ $180 ° - 2 \cdot 32.3 °$
$γ$ $=$ $115.4 °$
alternatively:
$\cos (\frac{1}{2} γ)$ $=$ $\frac{h_{c}}{b}$
$\frac{1}{2} γ$ $=$ $57.25 °$
$γ$ $=$ $115.4 °$
$\sin (\frac{1}{2} γ)$ $=$ $\frac{\frac{1}{2} c}{b}$
$\frac{1}{2} γ$ $=$ $57.25 °$ $\cdot 2$
$γ$ $=$ $115.4$

c = 35.4cm
$β$ = 43.9°

For this task you need the following basic knowledge: Triangle
Calculate the sides $a$ and $b$ of the triangle.
Use the cosine to calculate the two catheti,
$\cos (β)$ $=$ $\frac{\frac{1}{2} c}{a}$ $\cdot a : \cos (β)$
$a$ $=$ $\frac{\frac{1}{2} \cdot 35.4 c m}{\cos (43.9 °)}$
$a$ $=$ $24.565 c m$
$=$ $b$
Calculate the height of the triangle:
You may use the sine to do this.
$\sin (β)$ $=$ $\frac{h_{c}}{a}$ $\cdot a$
$h_{c}$ $=$ $\sin (43.9 °) \cdot 24.565 c m$
$h_{c}$ $=$ $17.033 c m$
↓
Calculate the two missing angles with sine or cosine .
$=$
$\cos (α)$ $=$ $\frac{\frac{1}{2} c}{b}$
$α$ $=$ $43.9 °$
or:
$\sin (α)$ $=$ $\frac{h_{c}}{b}$
$α$ $=$ $43.9 °$
↓
Add the two angles and subtract them from the sum of the angles in the triangle to calculate the last angle.
$=$
$γ$ $=$ $180 ° - 2 \cdot 43.9 °$
$=$ $92.2 °$
alternatively:
$\cos (\frac{1}{2} γ)$ $=$ $\frac{h_{c}}{b}$
$\frac{1}{2} γ$ $=$ $46.1 °$ $\cdot 2$
$γ$ $=$ $92.2 °$
$\sin (\frac{1}{2} γ)$ $=$ $\frac{\frac{1}{2} c}{b}$
$\frac{1}{2} γ$ $=$ $46.1 °$ $\cdot 2$
$γ$ $=$ $92.2 °$

$h_{c}$ = 14.8cm
$α$ = 28.3°

For this task you need the following basic knowledge: Triangle
Calculate the sides a and b of the triangle:
You may use the sine to do this.
$\sin (α)$ $=$ $\frac{h_{c}}{b}$ $\cdot b : \sin (α)$
$b$ $=$ $\frac{14.8 c m}{\sin (28.3 °)}$
$b$ $=$ $31.218$
$=$ $a$
Calculate the side $c$ of the triangle:
You may use the cosine to do this.
$\cos (α)$ $=$ $\frac{\frac{1}{2} c}{b}$ $\cdot b$
$\cos (28.3 °) \cdot 31.218 c m$ $=$ $\frac{1}{2} c$ $\cdot 2$
$c$ $=$ $54.973 c m$
↓
Calculate the missing angles using cosine or sine,
$=$
$\cos (β)$ $=$ $\frac{\frac{1}{2} c}{a}$
$β$ $=$ $28.3 °$
or:
$\sin (β)$ $=$ $\frac{h_{c}}{a}$
$β$ $=$ $28.3 °$
↓
Add the two angles and subtract them from the sum of the angles in the triangle to work out the last angle.
$=$
$γ$ $=$ $180 ° - 2 \cdot 28,3 °$
$γ$ $=$ $123,4 °$
alternatively:
$\cos (\frac{1}{2} γ)$ $=$ $\frac{h_{c}}{b}$
$\frac{1}{2} γ$ $=$ $61,7 °$ $\cdot 2$
$γ$ $=$ $123,4 °$
or:
$\sin (\frac{1}{2} γ)$ $=$ $\frac{\frac{1}{2} c}{b}$
$\frac{1}{2} γ$ $=$ $61,7 °$ $\cdot 2$
$γ$ $=$ $123,4 °$

a = 146.4m
$h_{c}$ = 58.4m

For this task you need the following basic knowledge: Triangle
Calculate the angle $α$ .
You may use the sine to do this.
$\sin (α)$ $=$ $\frac{h_{c}}{b}$
$α$ $=$ ${23.51}^{\circ}$
Now calculate the side $c$ using the cosine.
$\cos (α)$ $=$ $\frac{\frac{1}{2} c}{b}$ $\cdot b$
$\frac{1}{2} c$ $=$ $\cos (α) \cdot b$
$\frac{1}{2} c$ $=$ $134.25 m$ $\cdot 2$
$c$ $=$ $268.5 m$
Calculate the remaining angles using sine or cosine.
$\cos (β)$ $=$ $\frac{\frac{1}{2} c}{a}$
$β$ $=$ ${23.51}^{\circ}$
or:
$\sin (β)$ $=$ $\frac{h_{c}}{a}$
$β$ $=$ ${23.51}^{\circ}$
Add the two angles and subtract them from the sum of the angles in the triangle.
$γ$ $=$ $180^{\circ} - 2 \cdot {23.51}^{\circ}$
$=$ ${132.98}^{\circ}$
alternatively:
$\cos (\frac{1}{2} γ)$ $=$ $\frac{h_{c}}{b}$
$\frac{1}{2} γ$ $=$ ${66.49}^{\circ}$ $\cdot 2$
$γ$ $=$ ${132.98}^{\circ}$
or:
$\sin (\frac{1}{2} γ)$ $=$ $\frac{\frac{1}{2} c}{b}$
$\frac{1}{2} γ$ $=$ ${66.49}^{\circ}$ $\cdot 2$
$γ$ $=$ ${132.98}^{\circ}$
9
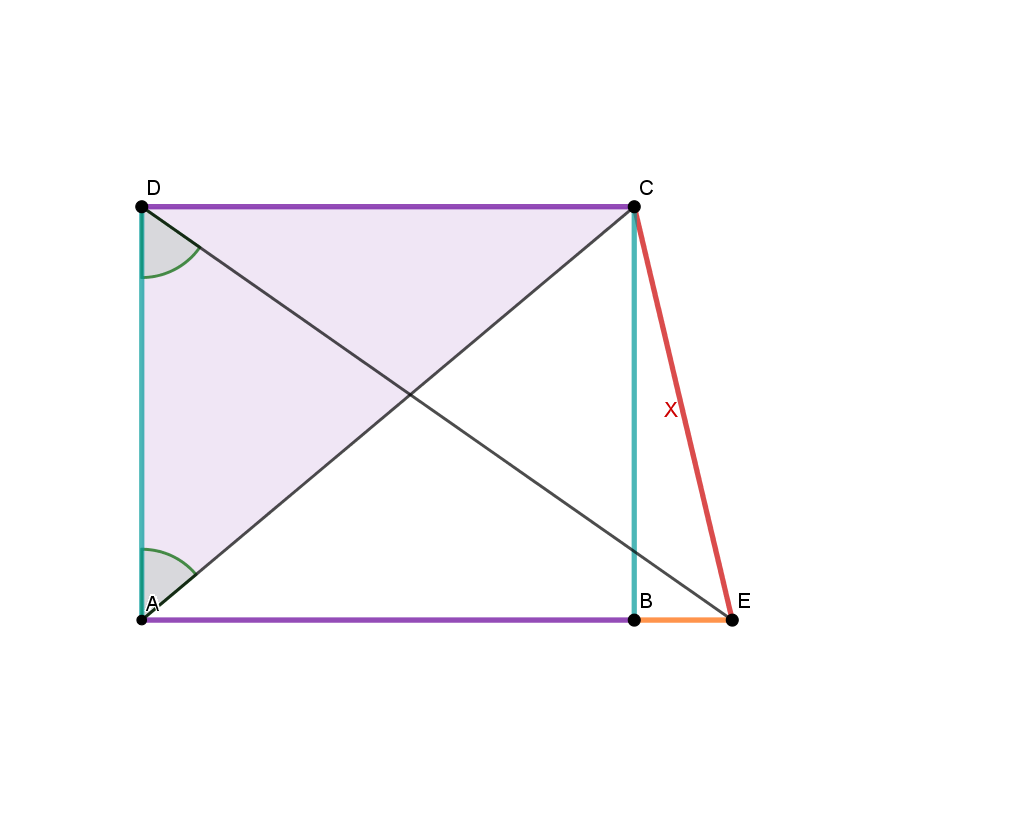
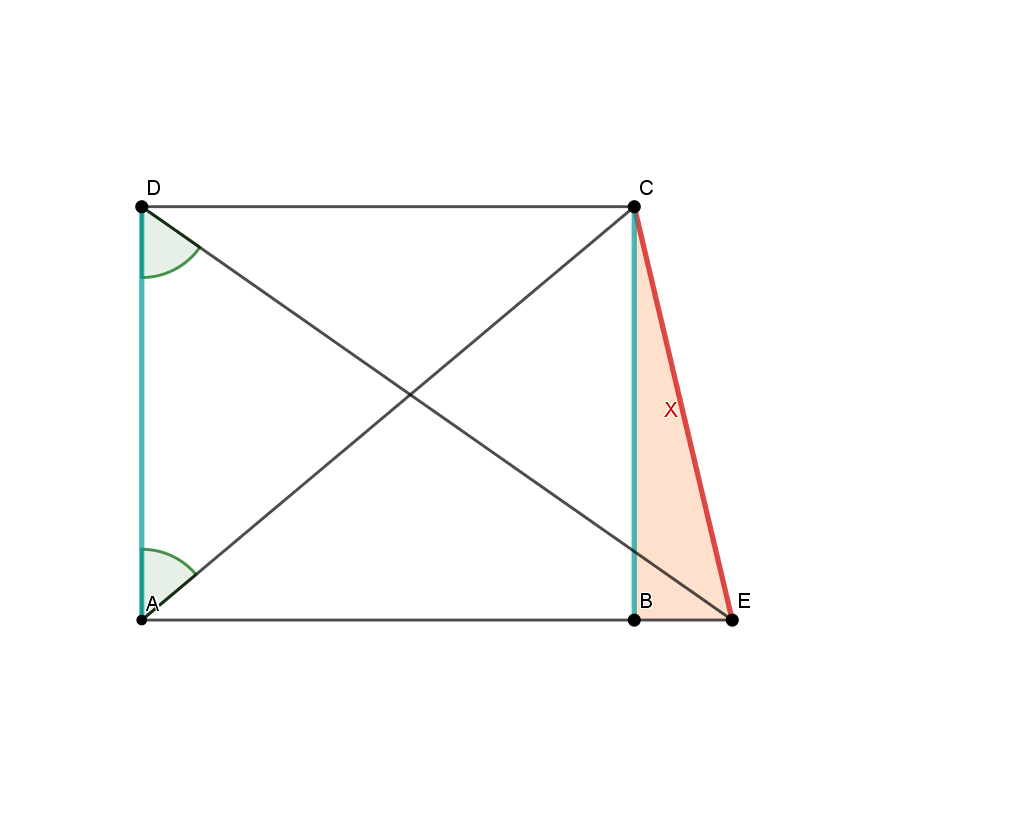
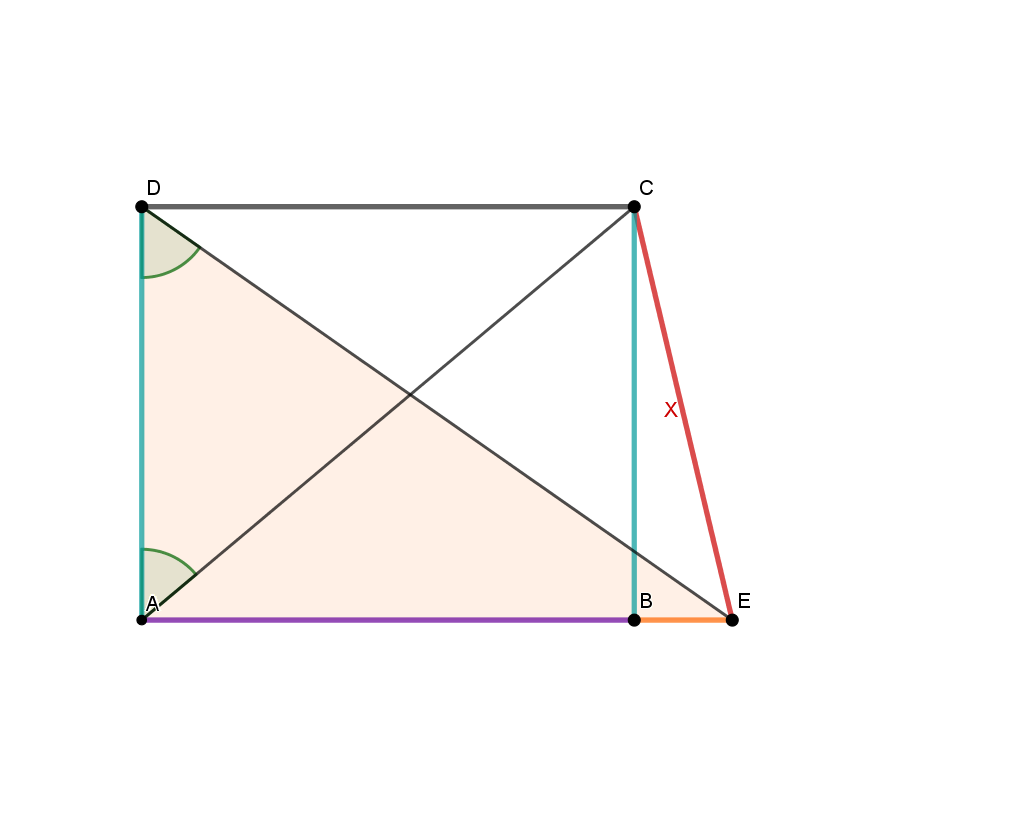
This sketch, which is not to scale, shows a trapezoid with the lengths:
$AD = 7 m, ∡ DAB = ∡ DCB = ∡ CDA = 90^{\circ}, ∡ CAD = 50^{\circ}, ∡ ADE = 55^{\circ}$
Calculate the distance of $x$

For this task you need the following basic knowledge: Sine, Cosine and Tangent
Hint: Proceed backwards in pictures:
For this exercise, you need to be able to use the sine and cosine in the right triangle and the Pythagorean theorem.
Strategy
If you want to work out a strategy for the solution first, it is best to work backwards:
To calculate the length of $x$ , for example, you need all the other distances in this triangle. You know the length of $B C$ . It is the same length as that of $A D$ , because they are opposite sides in a rectangle. That means you only have to determine $B E$ .
$B E$ can be calculated by subtracting the length of $A B$ from the long side $A E$ . You can calculate $A E$ with the using the tangent in the triangle $Δ A D E$ . To calculate $A B$ , for example, you can use the tangent in the triangle $Δ A C D$ , because you know that $D C$ and $A B$ , as opposite sides in the rectangle, have the same length.
Lösung
Nun kennst du das Vorgehen "von hinten" und kannst es in genau umgekehrter Reihenfolge verwenden, um auf die Länge der Strecke $x$ zu kommen:
Berechnung von $D C$
Verwende den Tangens im Dreieck $Δ A C D$ mit dem dir bekannten Winkel $∡ CAD$ für die Berechnung von $D C$ :
Solution
Now you know the procedure "from behind" and can use it in exactly the opposite order to arrive at the length of $x$ :
Calculation of $D C$
Use the tangent in the triangle $Δ A C D$ with the known angle $∡ CAD$ to calculate $D C$ :
$\tan (∡ CAD) = \frac{opposite cathetus}{adjacent cathetus} = \frac{D C}{A D}$
Solve for $D C$ by multiplying both sides with $A D$ .
$D C = A D \cdot \tan (∡ CAD)$
Plug in the values $AD = 7 m$ and $∡ CAD = 50^{\circ}$ .
$D C = A B = 7 \cdot \tan (50^{\circ}) \approx 8.34$
Computing $A E$
Use the tangent in the triangle $Δ A D E$ to calculate $A E$ , since you know $∡ ADE = 55^{\circ}$ and $A D = 7$ .
$\tan (∡ ADE) = \frac{opposite cathetus}{adjacent cathetus} = \frac{A D}{A E}$
Solve for $A E$ by multiplying with $A E$ and dividing by $\tan (∡ ADE)$ .
$A E = \frac{A D}{\tan (∡ ADE)}$
Plug in the values.
$A E = \frac{7}{\tan (55^{\circ})} \approx 10.00$
Computing $B E$
Now you can compute $B E$ :
$B E = A E - A D = 10.00 - 8.34 = 1.66 m$
Computing $x$
Now you can calculate the length of $x$ using the Pythagorean theorem. Here $x$ is the hypotenuse.
$x^{2} = {B E}^{2} + {B C}^{2}$
Solve for $x$ by taking the root.
$x = \sqrt{{B E}^{2} + {B C}^{2}}$
Plug in the values. Remember that you can use $B C = A D$ because they are opposite sides in the rectangle.
$x = \sqrt{{1.66}^{2} + 7^{2}} \approx 7.19 m$
The side $x$ is $7.19 m$ long.
Here, as is very often the case, there is not only one possible solution. For example, you can also use the sine or cosine instead of the tangent with another intermediate step.
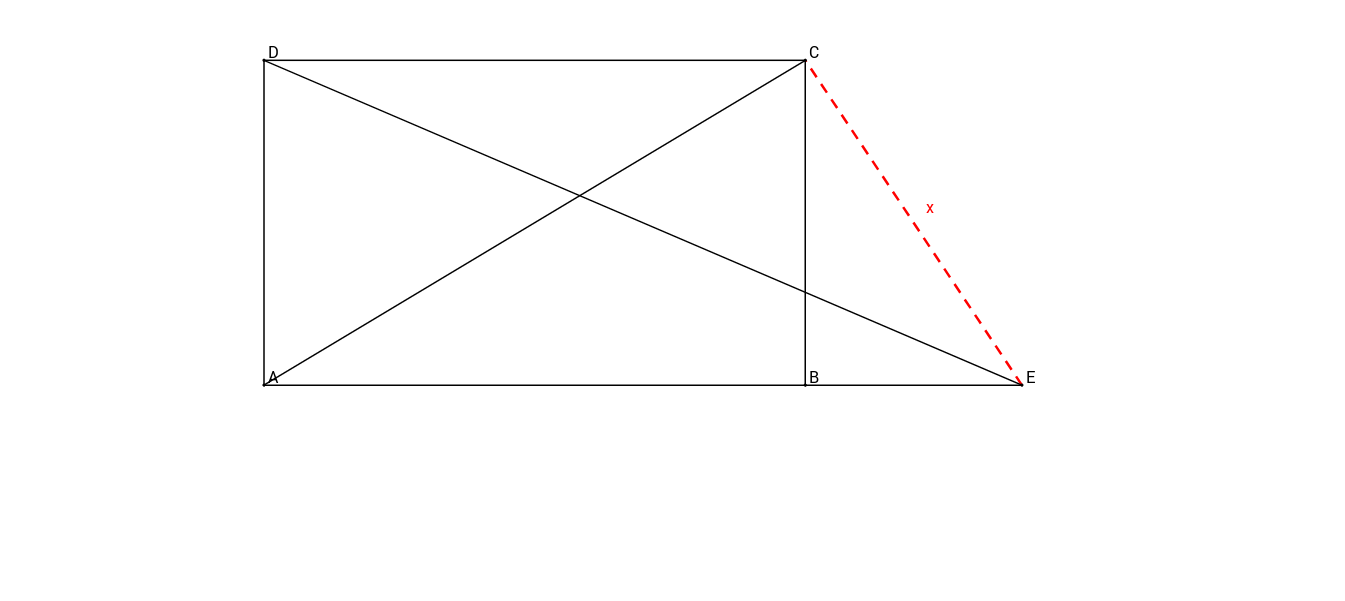
10
This sketch, which is not to scale, shows a kite quadrilateral $A B C D$ with symmetry axis $A C$ and the sides: $a = 7 cm$ , $c = 6 cm$ , $DB = 10 cm$
Compute the angles $α, β$ and $γ$ .

Solution is still missing
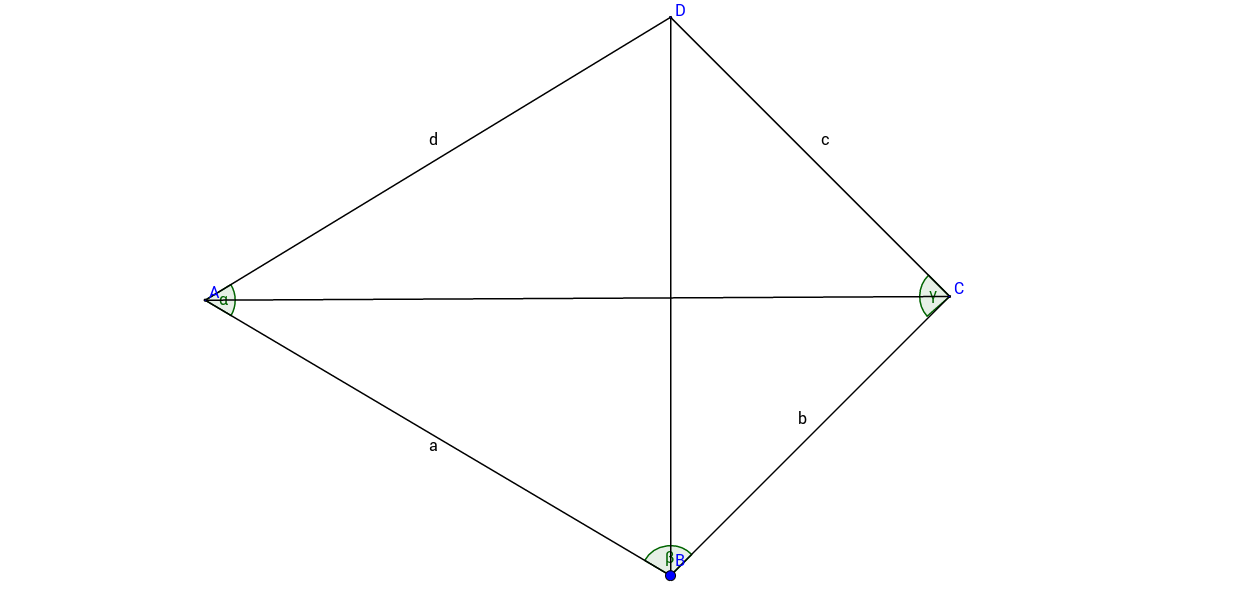
11
This sketch, which is not to scale, shows a rectangle with side lengths $a = 5.0 cm$ and $b = 7.0 cm$ .
Calculate the angle $α$ .

For this task you need the following basic knowledge: Sine, Cosine and Tangent
First, draw a sketch.
Draw a rectangle and point out the angle $α$ .
If you now draw a line from the intersection of the diagonals to the centre of the side $[B C]$ , then the angle $α$ you are looking for is divided into two equal parts by this auxiliary line.
There are several ways to calculate the angle $\frac{α}{2}$ :
You may compute $\frac{α}{2}$ using the sine.
You may compute $\frac{α}{2}$ using the tangent.
The solution with the tangent is mathematically easier .
Solution with the sine
First we calculate the distance from $A$ to $C$ and thus obtain a right-angled triangle.
$\begin{array}{rcl} A C & = & \sqrt{b^{2} + a^{2}} \\ A C & = & \sqrt{(7 cm)^{2} + (5 cm)^{2}} \\ A C & = & \sqrt{74} cm \end{array}$
To calculate the angle $α$ , we divide the distance from $A$ to $C$ and the distance from $A$ to $B$ by $2$ . Thus we can apply the sine to calculate $\frac{α}{2}$ . Then we multiply the calculated angle by $2$ and get the angle we are looking for, $α$ .
$\frac{A B}{2} = \frac{5 cm}{2} = 2.5 cm \frac{A C}{2} = \frac{\sqrt{74}}{2} cm \sin (\frac{α}{2}) = \frac{\frac{A B}{2}}{\frac{A C}{2}} = \frac{2.5}{\frac{\sqrt{74}}{2}} α = 2 \cdot \sin^{- 1} (\frac{2.5}{\frac{\sqrt{74}}{2}}) \approx 71 °$
Solution with the tangent
Consider the triangle $Δ M M_{B C} C$ . This triangle is right-angled.
The side $[M M_{B C}]$ is the adjacent cathetus of $\frac{α}{2}$ .
The side $[M_{B C} C]$ is the opposite cathetus of $\frac{α}{2}$ .
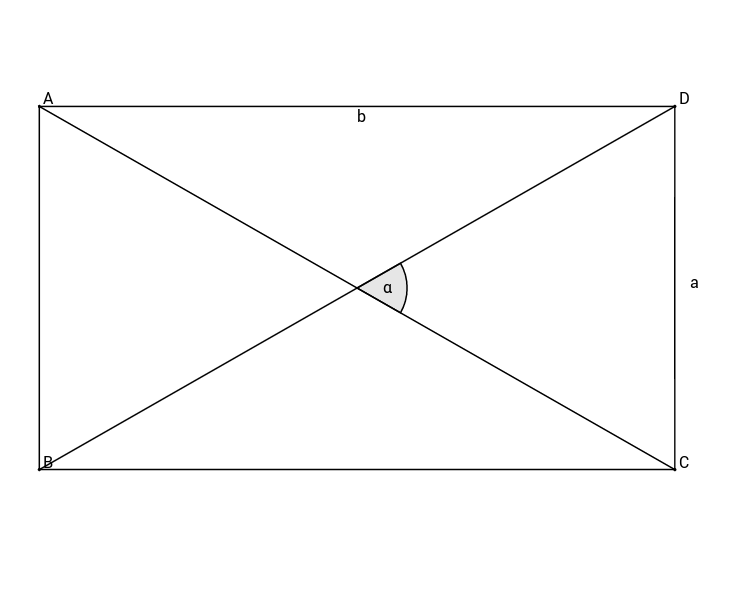
12
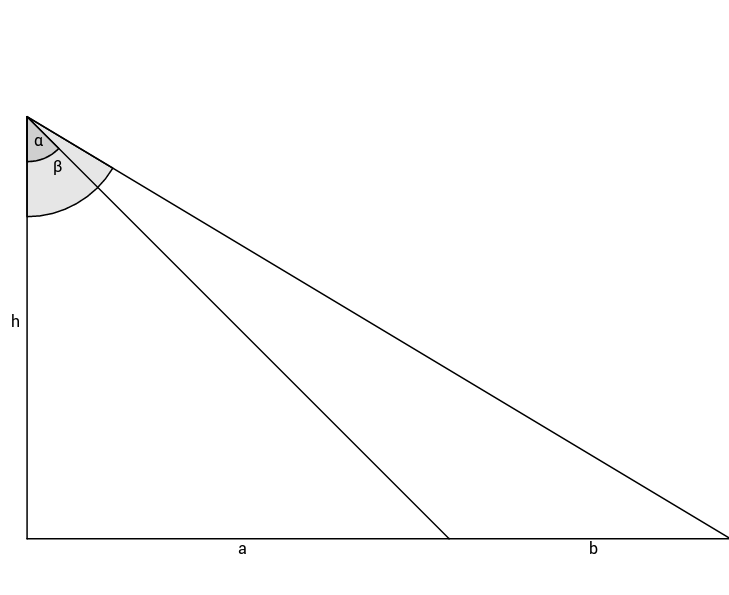
This sketch shows a right triangle, not true to size, with height $h = 8 cm$ and angles $α = 65^{\circ}$ and $β = 80^{\circ}$ .
Calculate the side lengths $a$ and $b$ .
$\begin{array}{l} a = \tan (α) \cdot h \\ a = \tan (65^{\circ}) \cdot 8 cm \\ a = 17.16 cm \\ b = \tan (β) \cdot h \\ b = \tan (80^{\circ}) \cdot 8 cm \\ b = 45.37 cm \end{array}$

Solution is still missing.

$\tan (α)$	$=$	$\frac{a}{b}$	$\cdot b : \tan (α)$
	↓	Solve for b
$b$	$=$	$\frac{a}{\tan (α)}$
	↓	Plug in $a = 5 cm$ and $α = 75 °$
$b$	$=$	$\frac{5 cm}{\tan (75^{\circ})}$
$b$	$=$	$1.34 cm$

$h$	$=$	$\sqrt{a^{2} - x^{2}}$
	↓	Plug in known values.
	$=$	$\sqrt{{(44.2 c m)}^{2} - {(31.7 c m)}^{2}}$
	↓	square
	$=$	$\sqrt{1953.64 c m^{2} - 1004.89 c m^{2}}$
	↓	subtract
	$=$	$\sqrt{948.75 c m^{2}}$
	↓	take the root
	$=$	$30.8 c m$

$\sin (α)$	$=$	$\frac{h}{b}$
	↓	Plug in known values.
	$=$	$\frac{30.8 c m}{44.2 c m}$
	↓	Compute $α$ using a calculator.
$α$	$=$	$44.2 ° = β$
	↓	So we have a right triangle with $α = β$
	$=$

$γ$	$=$	$180 ° - 2 \cdot 44.2 °$
	↓	multiply and subtract
	$=$	$91.6 °$

$\sin (α)$	$=$	$\frac{h}{b}$
	↓	solve for $h$ and plug in values.
$h$	$=$	$114.5 m \cdot \sin (32.3 °)$
	↓	multiply
	$=$	$61.2 m$

$x$	$=$	$\sqrt{a^{2} - h^{2}}$
	↓	Plug in known values.
	$=$	$\sqrt{{(114.5 m)}^{2} - {(61.2 m)}^{2}}$
	↓	square
	$=$	$\sqrt{13110.25 m^{2} - 3745.44 m^{2}}$
	↓	subtract
	$=$	$\sqrt{9364.81 m^{2}}$
	↓	take the root
$x$	$=$	$96.8 c m$

$\cos (β)$	$=$	$\frac{x}{a}$
	↓	Solve for $a$ and plug in values.
$a$	$=$	$\frac{17.7 c m}{\cos (43.9 °)}$
	↓	divide
$a$	$=$	$24.6 c m$

$\tan (β)$	$=$	$\frac{h}{x}$
	↓	Solve for $h$ and plug in values.
$h$	$=$	$17.7 c m \cdot \tan (43.9 °)$
	↓	multiply
$h$	$=$	$17.0 c m$

$\tan (β)$	$=$	$\frac{h}{x}$
	↓	Solve for $x$ and plug in values.
$x$	$=$	$\frac{14.8 c m}{\tan (28.3 °)}$
	↓	divide
$x$	$=$	$27.5 c m$
	↓	You get $c$ by doubling side $x$ .
$c$	$=$	$2 \cdot 27.5 c m$
	$=$	$55 c m$

$\sin (α)$	$=$	$\frac{h}{b}$
	↓	Solve for $b$ and plug in values.
$b$	$=$	$\frac{14.8 c m}{\sin (28.3 °)}$
	↓	divide
	$=$	$31.2 c m$

$\sin (β)$	$=$	$\frac{h_{c}}{α}$
$β$	$\approx$	$44.177 °$

$\cos (\frac{1}{2} γ)$	$=$	$\frac{\frac{1}{2} c}{a}$
$\frac{1}{2} γ$	$\approx$	${45.8}^{°}$
$γ$	$\approx$	${45.8}^{\circ} \cdot 2 = {91.6}^{\circ}$

$\sin (\frac{1}{2} γ)$	$=$	$\frac{h_{c}}{a}$
$\frac{1}{2} γ$	$=$	$45.8 °$
$γ$	$=$	$2 \cdot 45.8 ° = 91.6 °$

$\cos (\frac{1}{2} γ)$	$=$	$\frac{h_{c}}{b}$
$\frac{1}{2} γ$	$=$	$57.25 °$
$γ$	$=$	$115.4 °$
$\sin (\frac{1}{2} γ)$	$=$	$\frac{\frac{1}{2} c}{b}$
$\frac{1}{2} γ$	$=$	$57.25 °$	$\cdot 2$
$γ$	$=$	$115.4$

$\sin (β)$	$=$	$\frac{h}{a}$
	↓	Plug in values and compute $α$
$β$	$=$	$23.5 °$

$\cos (39 °)$	$=$	$\frac{113 m}{c}$	$\cdot c$
	↓	Get c on one side
$c \cdot \cos (39 °)$	$=$	$113 m$	$: \cos (39 °)$
$c$	$=$	$\frac{113 m}{\cos (39 °)}$
$c$	$=$	$145 m$

$β + 90 ° + 39 °$	$=$	$180 °$
$β$	$=$	$180 ° - 90 ° - 39 °$
$β$	$=$	$51 °$

$\sin (39 °)$	$=$	$\frac{a}{145 m}$	$\cdot 145 m$
$a$	$=$	$\sin (39 °) \cdot 145 m$
$a$	$=$	$91 m$

$\sin (\frac{α}{2})$	$=$	$\frac{x}{r}$
	↓	Solve for $x$ and plug in values.
$x$	$=$	$10 c m \cdot \sin (\frac{84^{\circ}}{2})$
	↓	Compute $x$ .
$x$	$=$	$6.7 c m$
	↓	Since $x$ is half of the chord $s$ , double it to get the chord $s$ .
$s$	$=$	$2 \cdot 6.7 c m$
$s$	$=$	$13.4 c m$

$\cos (α)$	$=$	$\frac{\frac{1}{2} c}{b}$	$\cdot b$
$\cos (32.3 °) \cdot 114.5 m$	$=$	$\frac{1}{2} c$	$\cdot 2$
$2 \cdot (\cos (32.3 °) \cdot 114.5 m)$	$=$	$c$
$c$	$=$	$193.565$

$\cos (β)$	$=$	$\frac{\frac{1}{2} c}{a}$	$\cdot a : \cos (β)$
$a$	$=$	$\frac{\frac{1}{2} \cdot 35.4 c m}{\cos (43.9 °)}$
$a$	$=$	$24.565 c m$
	$=$	$b$

$\sin (β)$	$=$	$\frac{h_{c}}{a}$	$\cdot a$
$h_{c}$	$=$	$\sin (43.9 °) \cdot 24.565 c m$
$h_{c}$	$=$	$17.033 c m$
	↓	Calculate the two missing angles with sine or cosine .
	$=$

$\sin (α)$	$=$	$\frac{h_{c}}{b}$	$\cdot b : \sin (α)$
$b$	$=$	$\frac{14.8 c m}{\sin (28.3 °)}$
$b$	$=$	$31.218$
	$=$	$a$

$γ$	$=$	$180^{\circ} - 2 \cdot {23.51}^{\circ}$
	$=$	${132.98}^{\circ}$

Exercises: Sine, Cosine and Tangent on a right triangle

1. Make a sketch

2. Calculate

Strategy

Lösung

Berechnung von DC

Solution

Computing AE

Use the tangent in the triangle ΔADE to calculate AE, since you know ∡ADE=55∘ and AD=7.

Computing BE

Computing x

Solution with the sine

Solution with the tangent

Berechnung von $D C$

Computing $A E$

Use the tangent in the triangle $Δ A D E$ to calculate $A E$ , since you know $∡ ADE = 55^{\circ}$ and $A D = 7$ .

Computing $B E$

Computing $x$