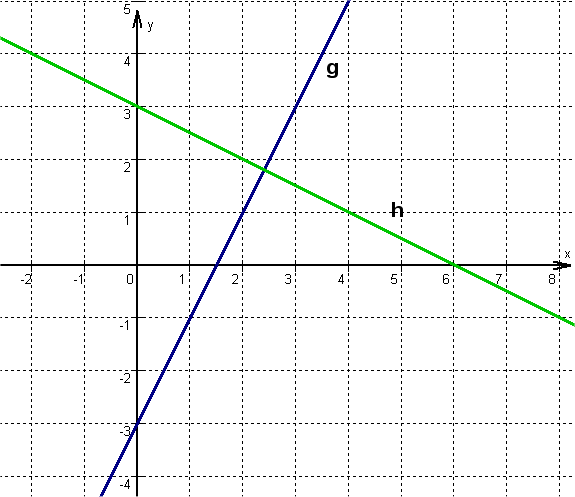
Checking with sketch

Select any point on the straight line, e.g. the $yy$-axis sections $(0\mathrm{\mid }-3)(0|-3)$ and $(0\mathrm{\mid }3)(0|3)$. Go from there 1 to the right and, corresponding to the slopes, $m_g=2m\_g=2$ upwards or $m_h=-0.5m\_h=-0.5$ downwards. Connect the two points to form a straight line.

If you look at the course of the straight line and, for example, the position of point $AA$, you will see that it will hardly lie on the straight line $hh$, but probably on $gg$. Similarly, you can decide for other points whether a mathematical check is worthwhile: Point $D(-102\mathrm{/}55)D(-102/55)$ can only lie on $hh$, for example.

Computational verification

Plug $A(1\mathrm{\mid }-1)A(1|-1)$ into $gg$:

Plug the coordinates y=-1 and x=1 into the equation.

$-1=2\cdot 1-3-1=2\backslash cdot1-3$

That is a true statement.

⇒ $AA$ is on $gg$.

$BB$ does not lie on any of the straight lines. This can be clearly seen in the sketch.

Plug $CC$ into $hh$:

$5=-0.5\cdot (-6)+35=-0.5\backslash cdot(-6)+3$

⇒ $5=3+35=3+3$

This statement is false, so $CC$ is not on $hh$.

Plug $DD$ into $hh$:

$55=-0.5\cdot (-102)+355=-0.5\backslash cdot\backslash left(-102\backslash right)+3$

⇒ $55=51+355=51+3$

This statement is false, so $DD$ is not on $hh$.

Plug $EE$ into $gg$:

$87=2\cdot 45-387=2\backslash cdot45-3$

This statement is correct, so $EE$ lies on $gg$.

Complete coordinates

$h:y=-0.5x+3h:\backslash ;y=-0.5x+3$ ; $P(5\mathrm{\mid }?)P(5|?)$

The given coordinate of the point (the $xx$-coordinate) is inserted into the function equation and the missing $yy$-coordinate is calculated from it.

$y=-0.5\cdot 5+3=-2.5+3=0.5y=-0.5\backslash cdot5+3=-2.5+3=0.5$

⇒ $P(5\mathrm{\mid }\mathrm{0,5})P(5|0\{,\}5)$

Q: $y=-0.5\cdot (-3.5)+3=1.75+3=4.75y=-0.5\backslash cdot(-3.5)+3=1.75+3=4.75$ $\Rightarrow \backslash ;\backslash ;\backslash Rightarrow\backslash ;\backslash ;$ $Q(-3.5\mathrm{\mid }4.75)Q(-3.5|4.75)$

R: $12=-0.5x+3\Rightarrow 0.5x=-9\Rightarrow x=-1812=-0.5x+3\backslash ;\backslash ;\backslash Rightarrow\backslash ;\backslash ;0.5x=-9\backslash ;\backslash ;\backslash Rightarrow\backslash ;\backslash ;x=-18$ $\Rightarrow \backslash ;\backslash ;\backslash Rightarrow\backslash ;\backslash ;$ $R(-18\mathrm{\mid }12)R(-18|12)$

S: $-7.5=-0.5x+3\Rightarrow 0.5x=10.5\Rightarrow x=21-7.5=-0.5x+3\backslash ;\backslash ;\backslash Rightarrow\backslash ;\backslash ;0.5x=10.5\backslash ;\backslash ;\backslash Rightarrow\backslash ;\backslash ;x=21$ $\Rightarrow \backslash ;\backslash ;\backslash Rightarrow\backslash ;\backslash ;$ $S(21\mathrm{\mid }-7.5)S(21|-7.5)$

Proof for $TT$

$T(2.4\mathrm{\mid }1.8)T(2.4|1.8)$

Plug the coordinates of $TT$ into both line equations. If the statements are true, $TT$ lies on the lines.

into $gg$:

into $hh$:

$\Rightarrow \backslash ;\backslash ;\backslash Rightarrow\backslash ;\backslash ;$ Both equations give correct statements, so the point $TT$ lies on both lines.

$\Rightarrow \backslash ;\backslash ;\backslash Rightarrow\backslash ;\backslash ;$ $TT$ Is the intersection point of the lines.