Solvability of Linear Systems

There are three possibilities for the number of solutions to a system of equations:

1. No solution

2. Exactly one solution

3. Infinitely many solutions.

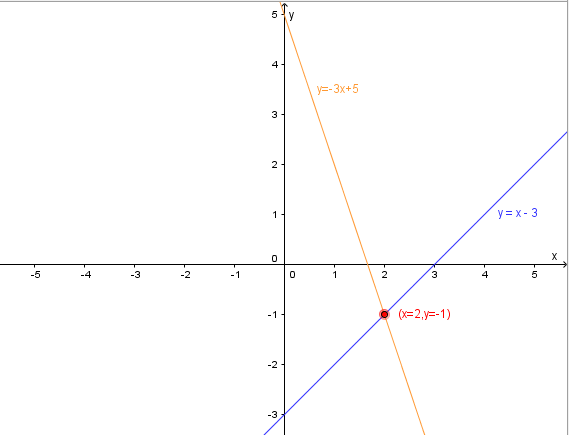
This can be easily illustrated with an example by graphing the system of equations:

Example

The graphs of the individual linear equations, i.e. the straight lines, intersect either:

• in a common point $\to$ one solution

• lie on top of each other (i.e. are equal) $\to$ infinitely many solutions, or

• are really parallel to each other, so they have no common point $\to$ no solution.

Determine solvability with the matrix representation

In the following, we consider quadratic linear systems of equations, that is, linear systems of equations with exactly as many equations as variables.

Procedure

The procedure is described here for a system of equations with three equations. However, it is also valid for systems of equations with more or less equations.

1. Representation as extended coefficient matrix

$\def\arraystretch{1.25} \begin{array}{ccccc}\mathrm{I}&x_1\cdot x&+y_1\cdot y&+z_1\cdot z&=b_1\\\mathrm{II}&x_2\cdot x&+y_2\cdot y&+z_2\cdot z&=b_2\\\mathrm{III}&x_3\cdot x&+y_3\cdot y&+z_3\cdot z&=b_3\end{array}\quad\to\quad\left(\begin{array}{ccc|c}x_1&y_1&z_1&b_1\\x_2&y_2&z_2&b_2\\x_3&y_3&z_3&b_3\end{array}\right)=(A|b)$

2. Bring to row echelon form

Bringing the expanded coefficient matrix to row echelon form means eliminating the coefficients $x_2$, $x_3$, $y_3$, for example using the Gaussian method.

$\def\arraystretch{1.25} \left(\begin{array}{ccc|c}x_1&y_1&z_1&b_1\\0&\tilde{y}_2&\tilde{z}_2&\tilde{b}_2\\0&0&\tilde{z}_3&\tilde{b}_3\end{array}\right)=(\tilde{A}|\tilde{b})$

3. Determine rank

The rank of a matrix is the number of rows in the row echelon form of the matrix that have at least one non-zero entry.

We write $rk(A)$ for the rank of the matrix $A$.

Determine the rank of the matrix $\def\arraystretch{1.25} \tilde{A}=\left(\begin{array}{ccc}x_1&y_1&z_1\\0&\tilde{y}_2&\tilde{z}_2\\0&0&\tilde{z}_3\end{array}\right)$ and the rank of the extended matrix $(\tilde{A}|\tilde{b}).$

4. Compare ranks

Now $n$ denotes the number of variables or the number of columns of the matrix. There are now three possibilities:

• $rk(\tilde{A})=rk(\tilde{A}|\tilde{b})=n$

  • Example: $\def\arraystretch{1.25} \left(\begin{array}{ccc|c}1&3&5&0\\0&2&1&1\\0&0&7&4\end{array}\right) \quad rk(\tilde{A})=3=rk(\tilde{A}|\tilde{b}),n=3$

  • Solvability: There is exactly one solution.

• $rk(\tilde{A})=rk(\tilde{A}|\tilde{b})<n$

  • Example: $\def\arraystretch{1.25} \left(\begin{array}{ccc|c}1&3&5&0\\0&2&1&1\\0&0&0&0\end{array}\right) \quad rk(\tilde{A})=2=rk(\tilde{A}|\tilde{b}),n=3$

  • Solvability: There are infinite solutions.

• $rk(\tilde{A})<rk(\tilde{A}|\tilde{b})$

  • Example: $\def\arraystretch{1.25} \left(\begin{array}{ccc|c}1&3&5&0\\0&2&1&1\\0&0&0&4\end{array}\right) \quad rk(\tilde{A})=2<3=rk(\tilde{A}|\tilde{b})$

  • Solvability: There is no solution.