Vertex of a Parabola

The vertex is the highest or lowest point (extreme point) of a parabola.

Properties of the vertex

• The vertex is the maximum of the function when the parabola is open downward and minimum of the function when the parabola is open upward.

• The parabola is axisymmetric to the parallel to the y-axis through the vertex.

Example

$f(x)=(x-2)^2+1$

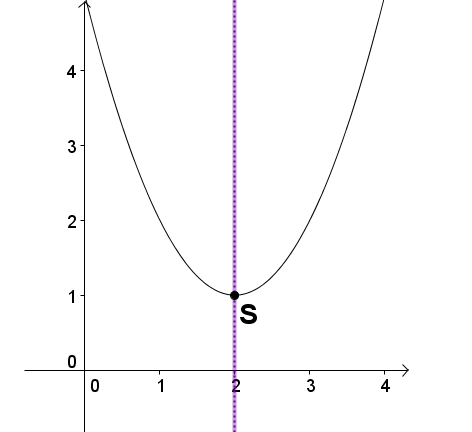
• The vertex is $S(2\vert1)$ and here is a minimum, because the parabola is open upwards.

• The parabola is axisymmetric to the straight line $x=2$.

Determination of the Vertex

There are four different methods for determining the apex:

• on the basis of the vertex shape

• using the general form

• using the derivative (advanced)

• using the zeros (not always applicable)

1. Determination on the basis of the vertex shape

If the function is already in vertex form (apex form), the point can be easily read:

• Vertex Shape: $f(x)=a(x-d)^2+e$

• Vertex: $S(d\vert e)$

Examples

Pay attention to the different signs of the functions!

• From the function $2\left(x-1\right)^2-3$ can be $d=1$ and $e=-3$ read off. The vertex is therefore located at point $S(1|-3)$.

• Is the function $\left(x-2\right)^2+4$, follows $d=2$ and $e=4$. Thus the vertex is at $S(2|4)$.

• Is the function $\left(x+1\right)^2+4$, follows $d=-1$ and $e=4$. Thus the vertex is at $S(-1|4)$.

Conversion to vertex form

If the equation is not yet in vertex form, you can convert it to vertex form with the quadratic addition or other transformations (multiply out, factor out, binomial formula) and then read off the vertex as already explained above.

2. Determination based on the general form

Using the following formula, you can also calculate the vertex directly from the general form.

• General Form: $f(x)=ax^2+bx+c$

Formula for the vertex:

$S\left(-\frac b{2~\cdot~ a}\left|c-\frac{b^2}{4 ~\cdot ~a}\right.\right)$

Example

The vertex of the function $f(x)=2x^2+x-3$ is to be determined using the formula.

$f(x)=2x^2+x-3$

Determine $a$, $b$, $c$ from the general form.

$a=2,~b=1,~c=-3$

$S\left(-\frac{1}{2\cdot2}\big|-3-\frac{1^2}{4\cdot2}\right)$

Summarize the terms by shortening and subtracting fractions.

$S\left(-\frac14\big\vert -\frac{25}{8}\right)$

Convert to general form

If the equation is not yet in the general form, you can bring it by transformations like multiply out, factoring out, binomial formula into the general form and then as already explained above, calculate the vertex by the formula.

3. Determination with the derivation (advanced)

The slope of the parabola is equal to 0 at the vertex. Therefore, the vertex of a parabola can also be calculated with the derivative, since the vertex is always the extremum of the quadratic function.

Example

It should be the vertex of $f(x)=x^2+2x+4$ can be calculated by means of the method determination with the derivative.

$f(x)=x^2+2x+4$

Directs the function $f$ from.

$f'(x)=2x+2$

Determine the zero of the first derivative for the extreme point, i.e. $f'(x)=0$.

$2x+2=0$

Solve for $x$.

$x=-1$

This is the extreme point. We have here a parabola opened upward, therefore $x=-1$ is the minimum digit. Calculate the corresponding y-value by adding $x=-1$ into the function:

$f(-1)=(-1)^2+2(-1)+4=1-2+4=3$

Write down the Vertex

$S~(-1~|~3)$

4. Determination based on the zeros

Caution. This method only works if the parabola has zeros.

If this is the case, the vertex lies exactly in the middle between these two zeros, because all parabolas are axisymmetric.

If the quadratic function has only one zero, then this is the x-value $x_s$ of the Vertex.

Example:

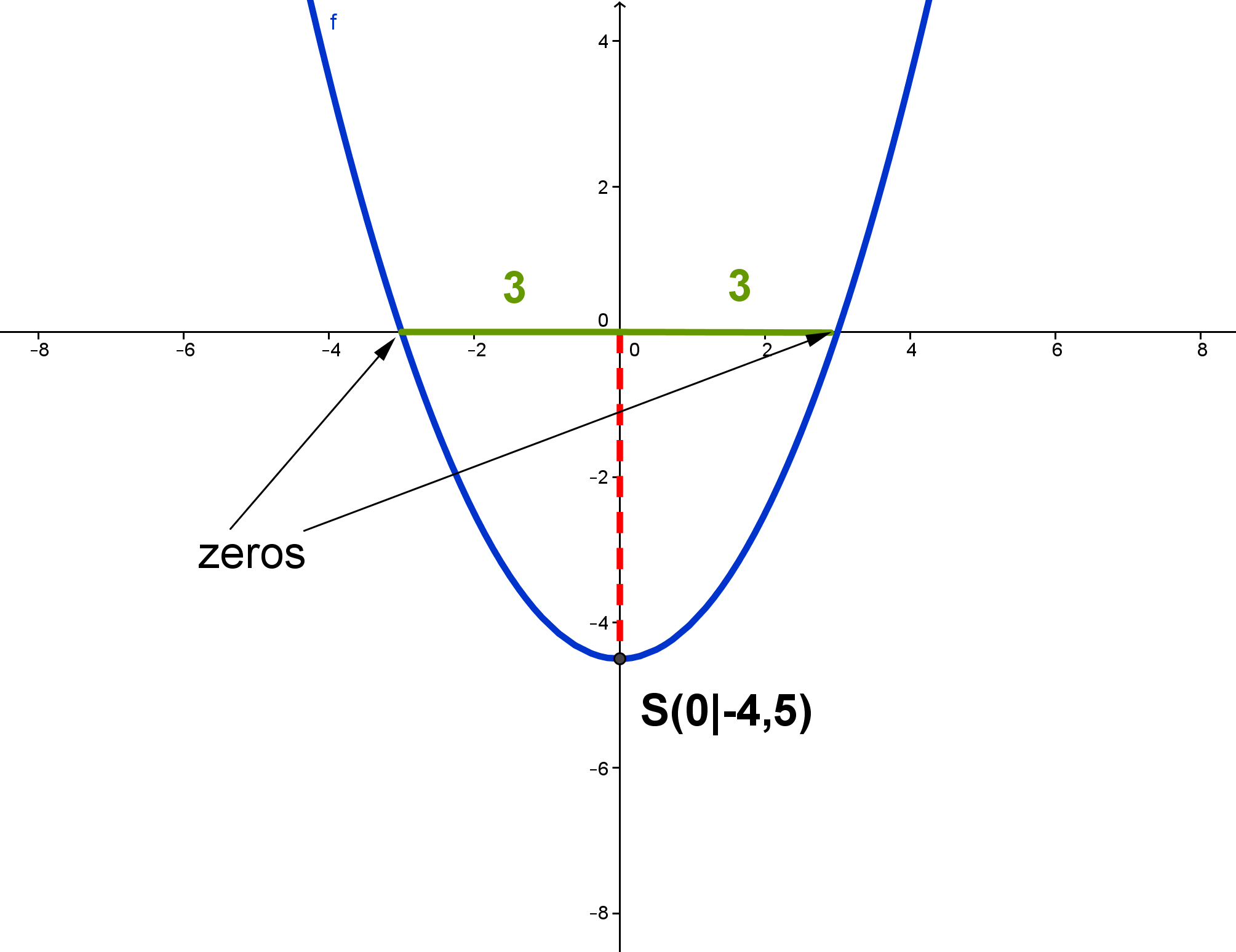
Determine the vertex of the function f with the function equation $f(x)= 0{,}5\cdot x^2-4{,}5$ using its zeros.

$f(x)=0{,}5\cdot x^2-4{,}5$

Calculate the zeros. of f.

$0=0{,}5\cdot x^2-4{,}5$

Add $4{,}5$.

$4{,}5=0{,}5\cdot x^2$

Multiply with $2$.

$9=x^2$

Draw the root.

$x=\pm\sqrt{9}$

Calculate the root.

$x_1=3$ and $x_2=-3$

The zeros of $f$are $-3$ and $3$.

The x-value of the vertex $x_s$ lies in the middle between these two zeros.The number 0 lies between$-3$ and $3$.

So, $x_s=0$.

Now determine the y-value of the vertex $y_s$, by substituting the x-value into the function equation of f .

$y_s=f(x_s)=f(0)=0{,}5\cdot0^2-4{,}5=-4{,}5$

The vertest of $f$ is $S(0|-4{,}5)$.

Graph of the function:

Video on how to determine the vertex using the zeros: