7How many solutions exist? (2/2)

How do you find out what solution type you have?

The three different solution types are explained with examples.

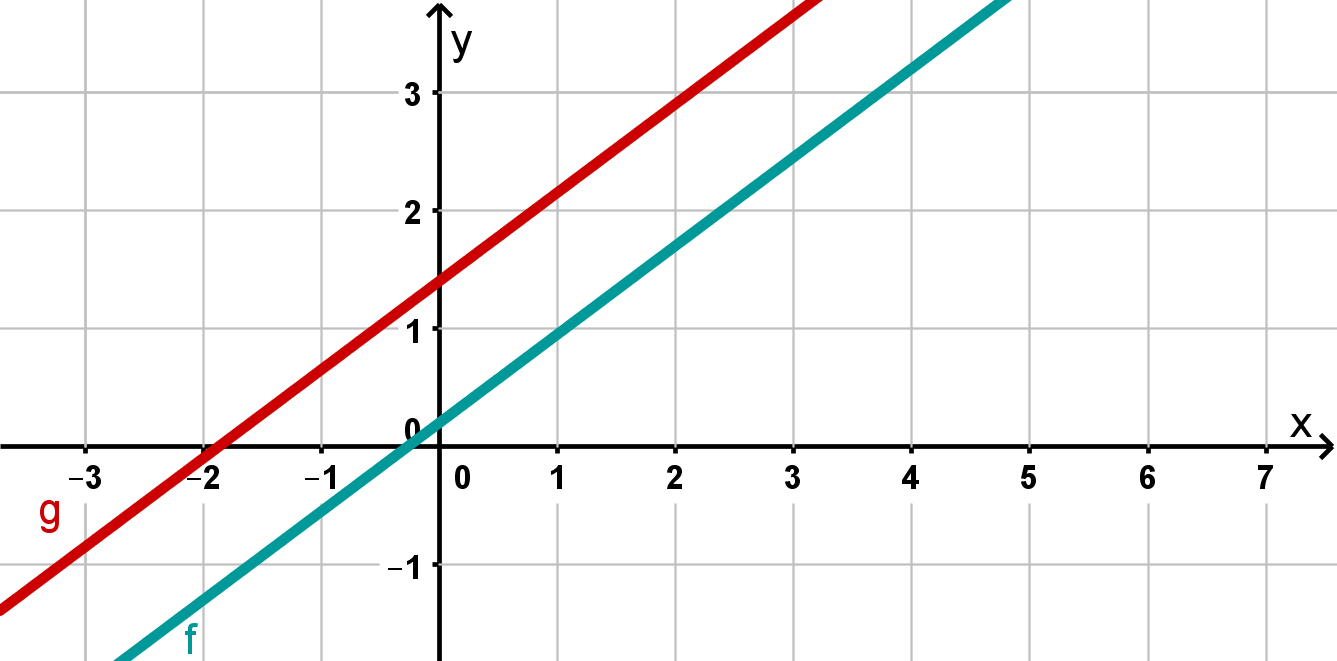
In the graphic you can see two parallel lines. You can see this because they have the same slope $\frac{3}{4}$, but different $y$-axis intercepts. The straight lines never intersect, so there is no solution.

In this case, the solution set is the empty set:

$\mathbb{L}=\{\}$ or $\mathbb{L}=\varnothing$.

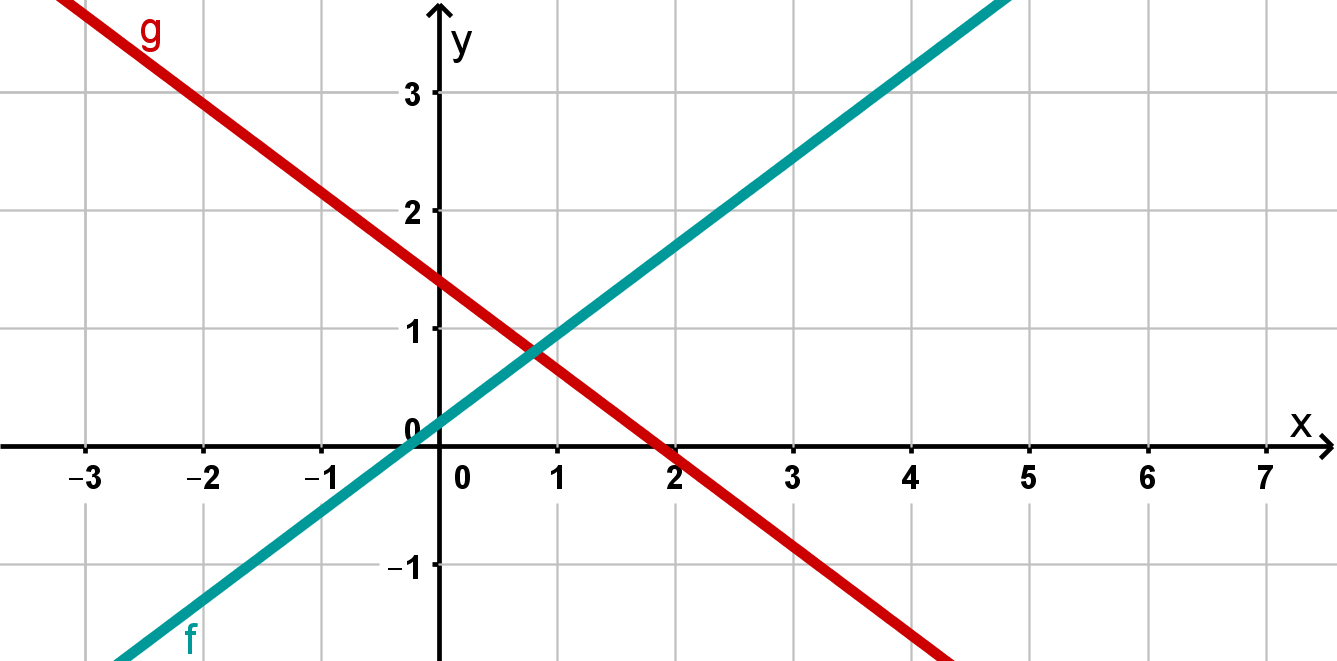
You can see from the graphic that the lines cross at an intersection point. This is always the case when both lines have different slopes. So there is exactly one solution.

The solution set here is simply again your number pair $\mathbb{L}=\{(x|y)\}$.

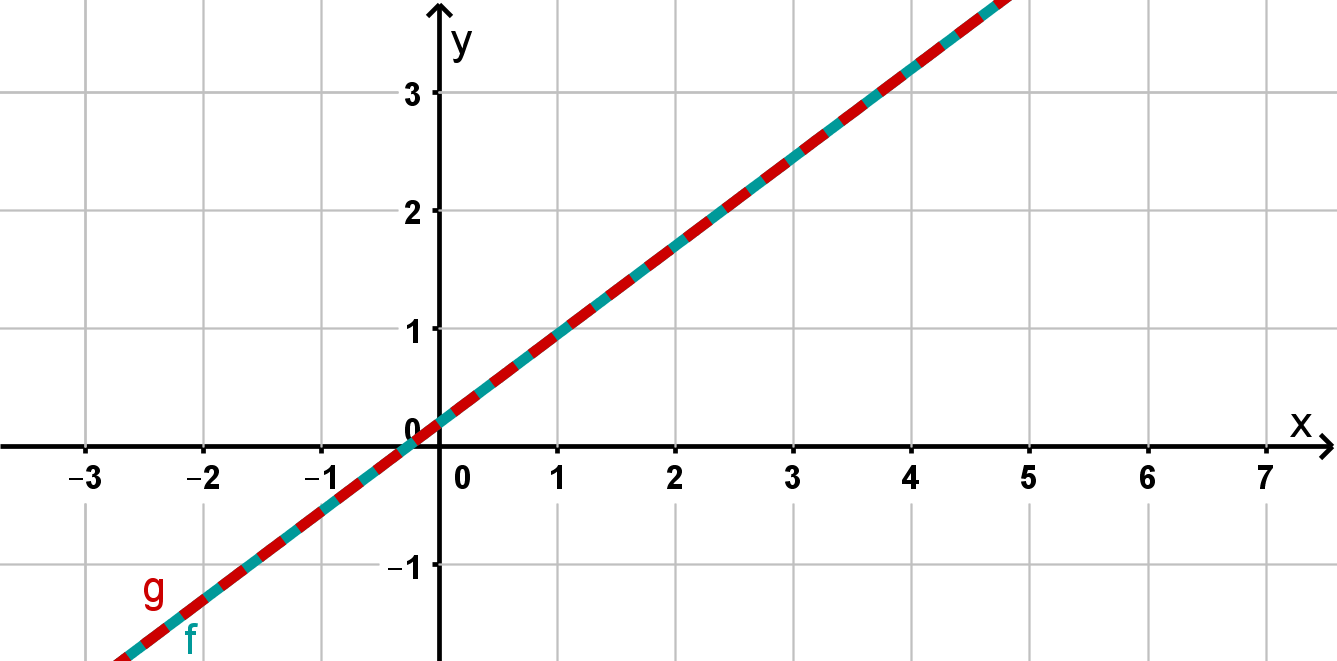
If you transform both equations, you will see that both lines have the same slope and the same $y$-axis intercept. They are therefore identical.

Every point on the lines is an intersection point. So there are infinitely many solutions.

The solution set here is the special case, namely: $\mathbb{L}=\left \{(x|y)\;\left |\;y=\dfrac{3}{4}x + \dfrac{1}{5}\right \}\right .$ , that is, all pairs of numbers $(x|y)$ with the property that they satisfy the equation $y = \frac{3}{4}x + \frac{1}{5}$.