Exercises: Sine and Cosine theorem
- 1
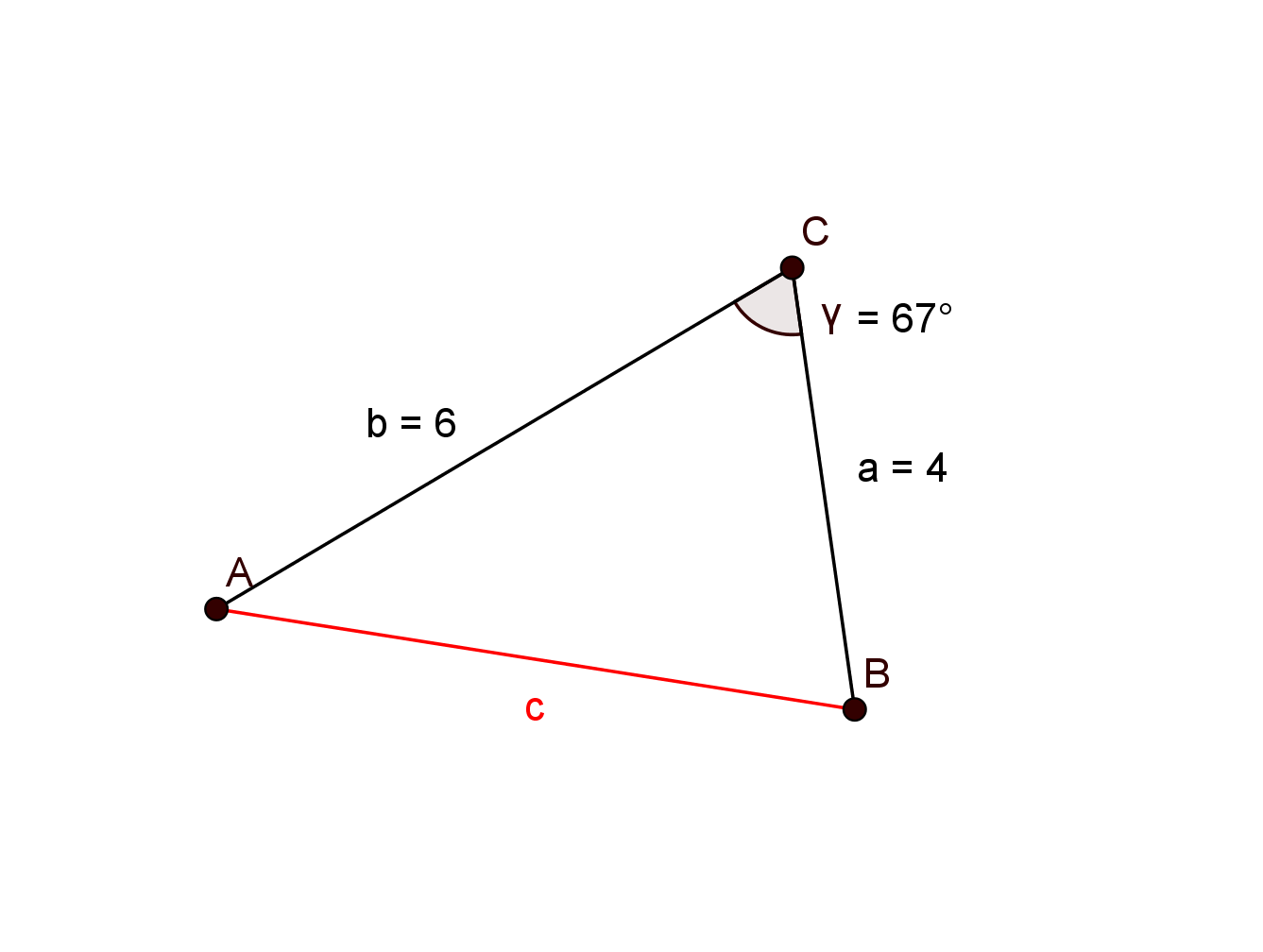
For this task you need the following basic knowledge: Cosine theorem
Given:
Required:
Use the cosine theorem.
↓ Plug in the given values.
↓ Add up the right-hand side.
- 2
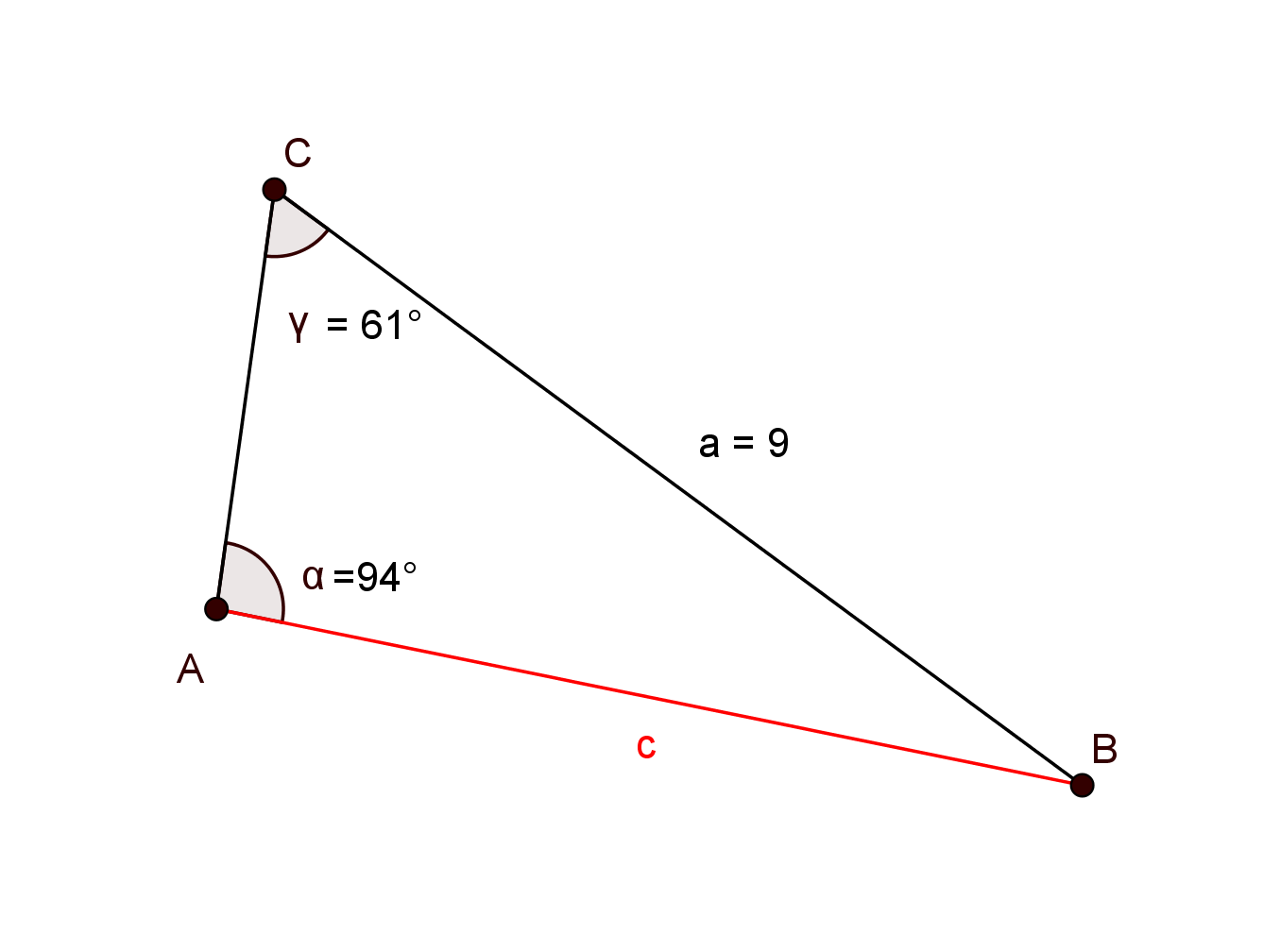
For this task you need the following basic knowledge: Sine theorem
Given:
Required:
You are given two angles and one side. Therefore use the sine theorem.
↓ Solve for the variable you are looking for. To do this multiply by .
↓ Plug in the values.
- 3
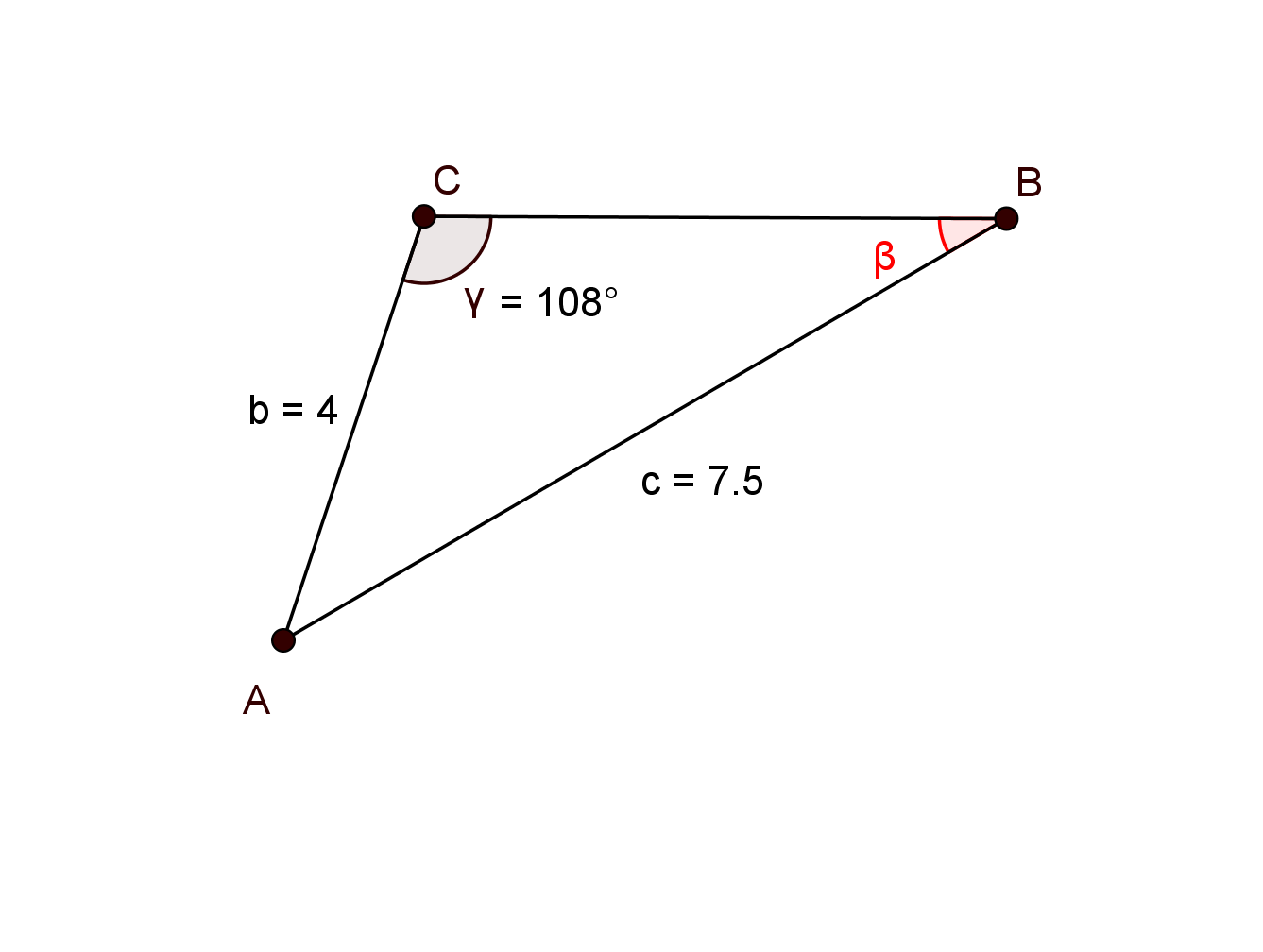
For this task you need the following basic knowledge: Sine theorem
Given:
Required:
You are given a pair of an angle and a side, as well as the side opposite the angle you are looking for. Therefore you may use the sine theorem.
↓ Hint: By forming the reciprocal value of both fractions, you can get the variable you are looking for into the numerator.
↓ Solve for the required variable.
↓ Plug in the given values.
- 4

For this task you need the following basic knowledge: Cosine theorem
Given:
Required:
You are given three sides and need to find the value of an angle. Since the angle you are looking for is the angle , the side standing alone in the cosine theorem is .
↓ Solve for .
↓ Plug in the given values.
- 5
The sketch shows a parallelogram with side lengths and , as well as the angle .
Calculate the angle .

For this task you need the following basic knowledge: Properties of a parallelogram
In particular, you need the following rules:
The diagonals in a parallelogram bisect each other.
Adjacent angles add up to .
Set up target equation
First we look for an equation that contains the angle we are looking for. In the parallelogram, only the side lengths and and the angle are known. Since the side a is opposite the angle we are looking for, the cosine theorem for is a good choice.
Since the diagonals bisect each other in a parallelogram, the sides adjacent to the angle have the length and respectively. The objective equation is therefore:

Simplify the target equation
To have to calculate less later, you can simplify the equation by factoring it out and shortening it
Calculate missing quantities
You can calculate the lengths of and with the cosine theorem:
In a parallelogram, adjacent angles add up to . So . Together with the supplement relations for sine and cosine, the following applies:
Insertion into the target equation
Insertion into the target equation :