Relations between trigonometric functions

Sine, cosine and tangent are in different relationships. A distinction is made between the complement relationships and the supplement relationships.

Complement relationships

$\sin (90^{\circ} - α) = \cos (α)$
$\cos (90^{\circ} - α) = \sin (α)$
$\tan (90^{\circ} - α) = \frac{1}{\tan (α)}$

Since in a triangle the sum of the interior angles is always $180 °$ , the following applies in a right triangle $β = 90 ° - α$ .

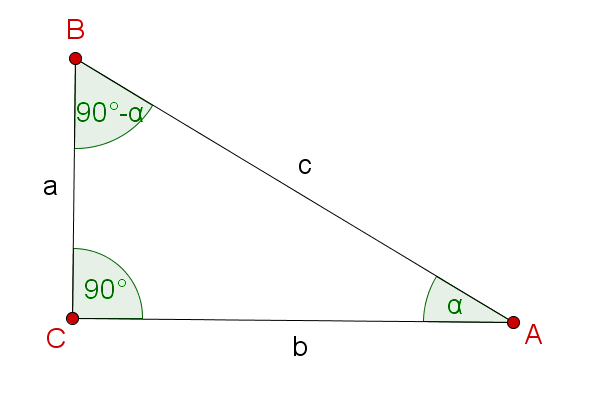
Using the sine, cosine and tangent formulas, you can see:

$\sin (90 ° - α) = \frac{opposite cathetus}{hypotenuse} = \frac{b}{c}$

$\cos (α) = \frac{adjacent cathetus}{hypotenuse} = \frac{b}{c} .$

Hence, $\sin (90 ° - α) = \cos (α)$ .

The other equations can be explained in the same way.

Example

Consider the given triangle. Calculate $\cos (α)$ in the same way as above.

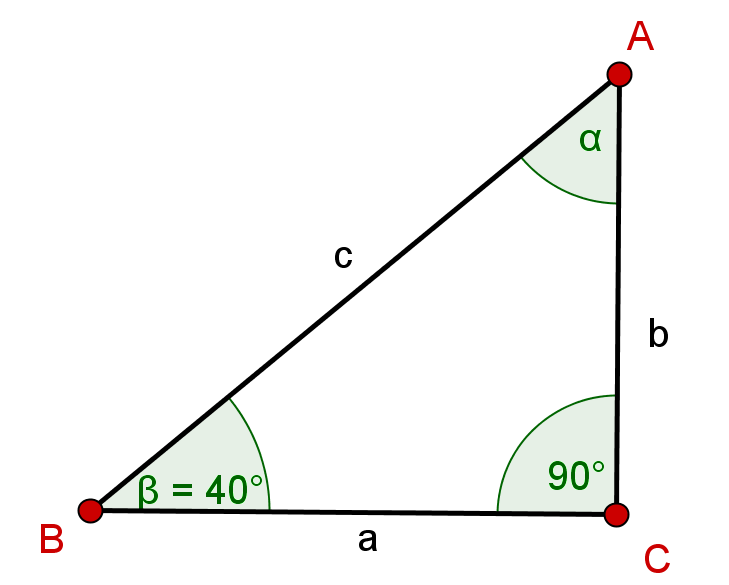
With the complement relation you can equate $\cos (α)$ and $\sin (90 ° - α)$ .

$\cos (α) = \sin (90 ° - α)$

Because of the sum of the interior angles, the following equation applies.

$\sin (90 ° - α) = \sin (β)$

Insert the value of $β$ , calculate the result and round it to $2$ decimal places.

$\sin (β) = \sin (40 °) \approx 0.59.$

Therefore, $\cos (α) \approx 0.59.$

Supplement relationships

Sine	Kosine	Tangent
$\sin (180 ° + α) = - \sin (α)$	$\cos (180^{\circ} + α) = - \cos (α)$	$\tan (180^{\circ} + α) = + \tan (α)$
$\sin (180 ° - α) = + \sin (α)$	$\cos (180 ° - α) = - \cos (α)$	$\tan (180^{\circ} - α) = - \tan (α)$
$\sin (360^{\circ} - α) = - \sin (α)$	$\cos (360^{\circ} - α) = + \cos (α)$	$\tan (360^{\circ} - α) = - \tan (α)$

Visualization

$\sin (180 ° + α) = - \sin (α)$ and $\cos (180 ° + α) = - \cos (α)$ can be tested, here

By clicking on image or button above you agree that external content from GeoGebra will be loaded. Also personal data may be transferred to this service in accordance with our privacy policy.

This content is licensed under
CC BY-SA 4.0 → What does that mean? serlo.org