Exercises: Sine, Cosine and Tangent on a right triangle
This sketch, which is not to scale, shows a trapezoid with the lengths:
Calculate the distance of
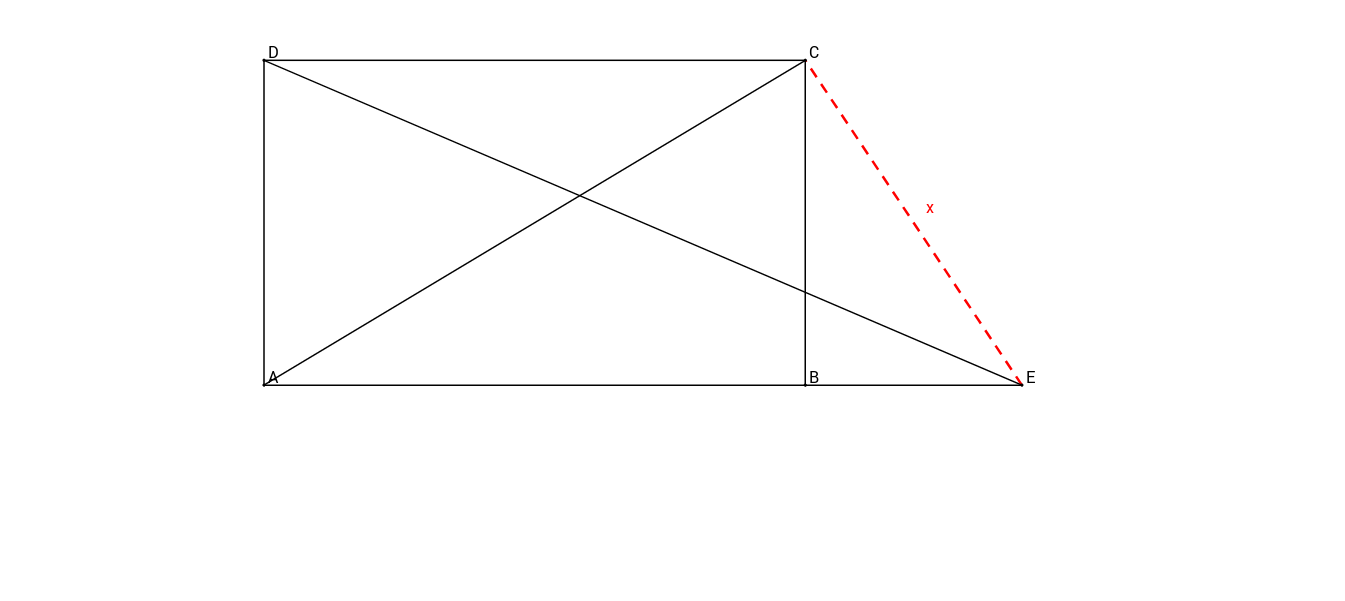
For this task you need the following basic knowledge: Sine, Cosine and Tangent
Hint: Proceed backwards in pictures:
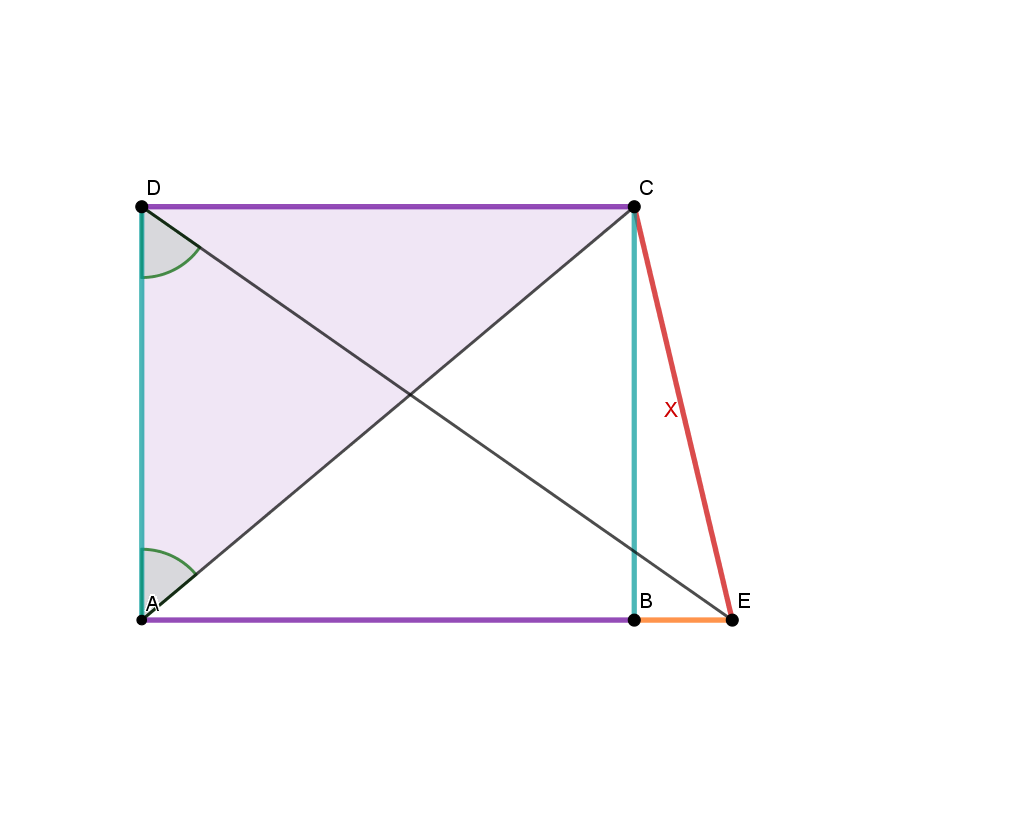
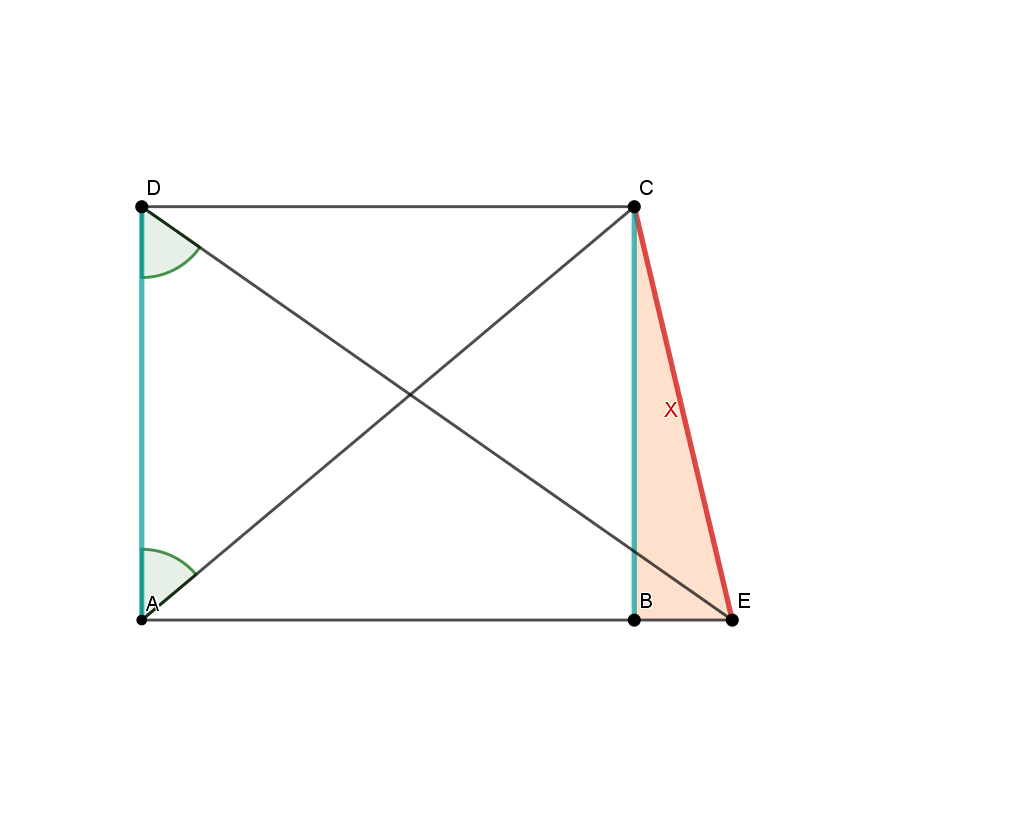
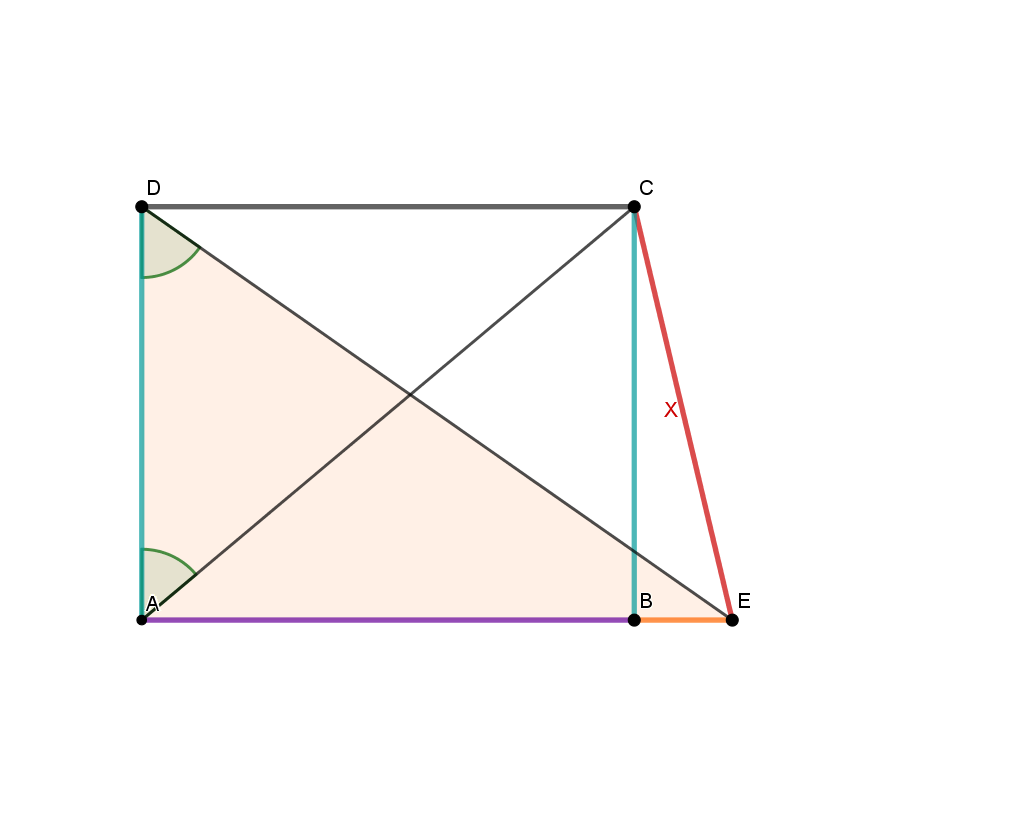
For this exercise, you need to be able to use the sine and cosine in the right triangle and the Pythagorean theorem.
Strategy
If you want to work out a strategy for the solution first, it is best to work backwards:
To calculate the length of , for example, you need all the other distances in this triangle. You know the length of . It is the same length as that of , because they are opposite sides in a rectangle. That means you only have to determine .
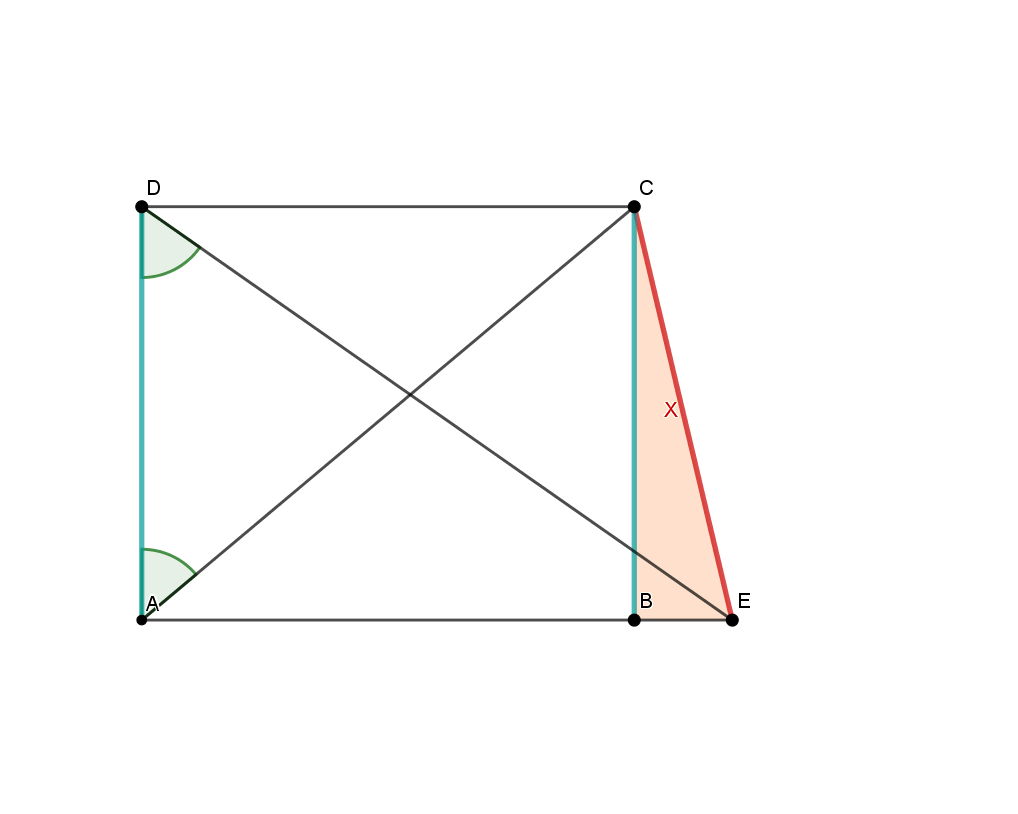
can be calculated by subtracting the length of from the long side . You can calculate with the using the tangent in the triangle . To calculate , for example, you can use the tangent in the triangle , because you know that and , as opposite sides in the rectangle, have the same length.
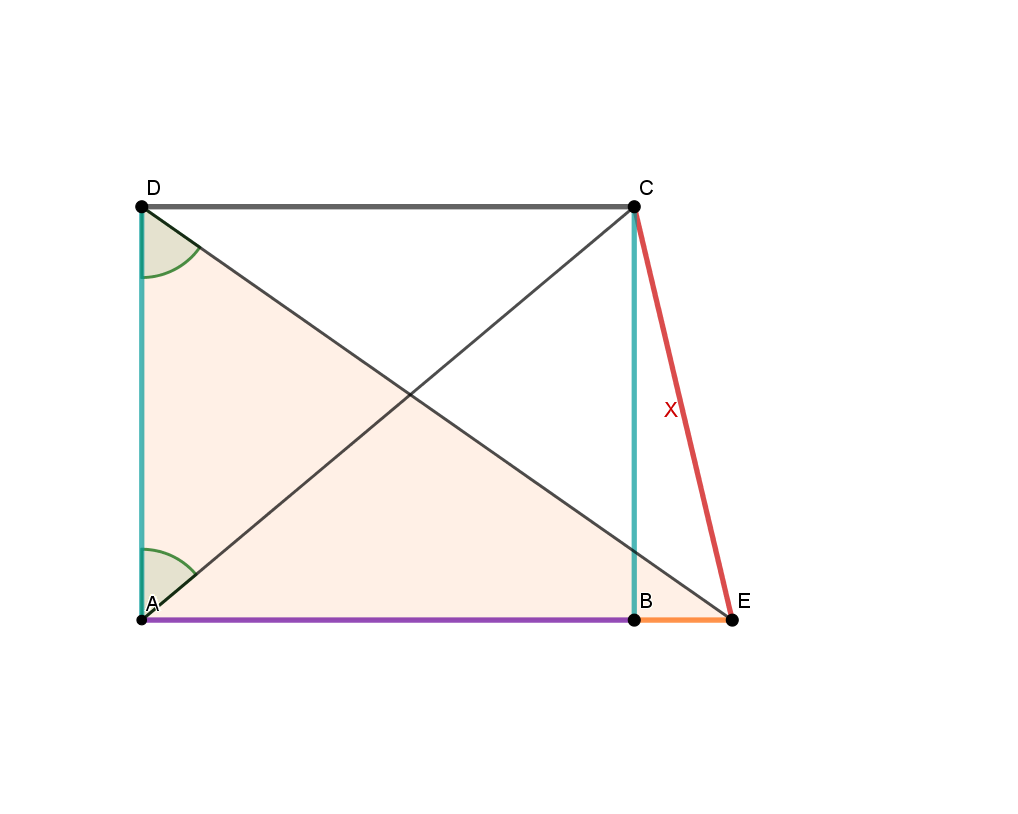
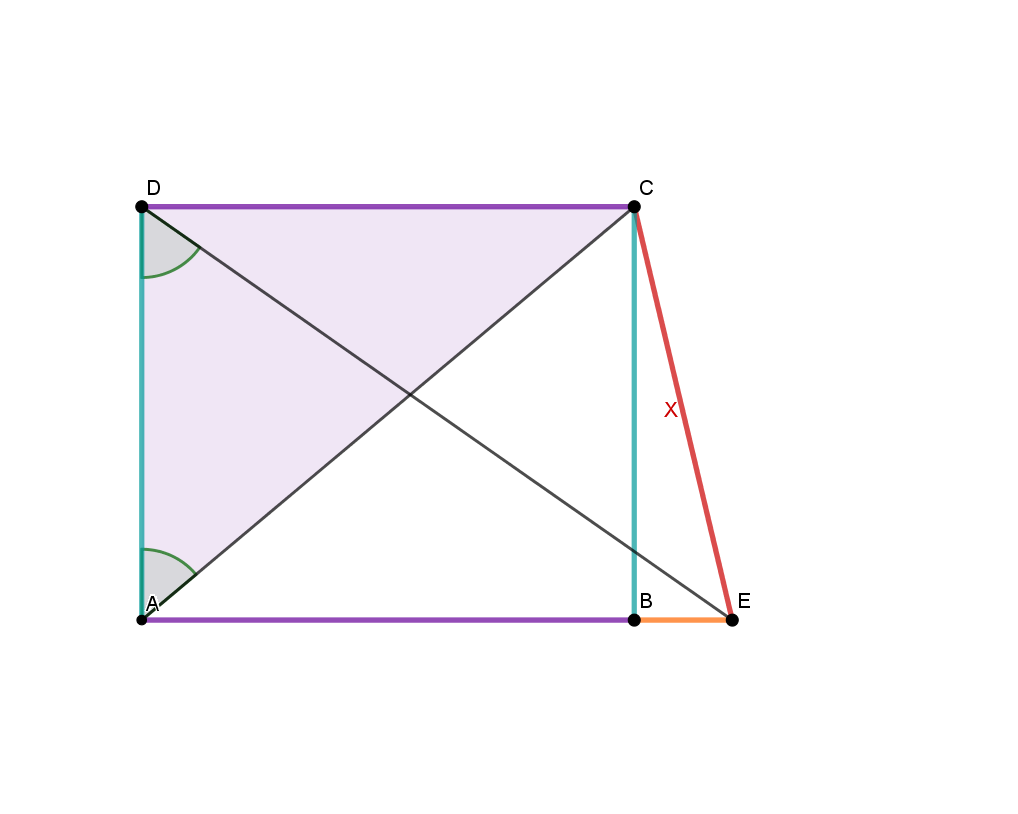
Lösung
Nun kennst du das Vorgehen "von hinten" und kannst es in genau umgekehrter Reihenfolge verwenden, um auf die Länge der Strecke zu kommen:
Berechnung von
Verwende den Tangens im Dreieck mit dem dir bekannten Winkel für die Berechnung von :
Solution
Now you know the procedure "from behind" and can use it in exactly the opposite order to arrive at the length of :
Calculation of
Use the tangent in the triangle with the known angle to calculate :
Solve for by multiplying both sides with .
Plug in the values and .
Computing
Use the tangent in the triangle to calculate , since you know and .
Solve for by multiplying with and dividing by .
Plug in the values.
Computing
Now you can compute :
Computing
Now you can calculate the length of using the Pythagorean theorem. Here is the hypotenuse.
Solve for by taking the root.
Plug in the values. Remember that you can use because they are opposite sides in the rectangle.
The side is long.
Here, as is very often the case, there is not only one possible solution. For example, you can also use the sine or cosine instead of the tangent with another intermediate step.