Exercises: Finding line equations
- 1
The following function graphs are given:
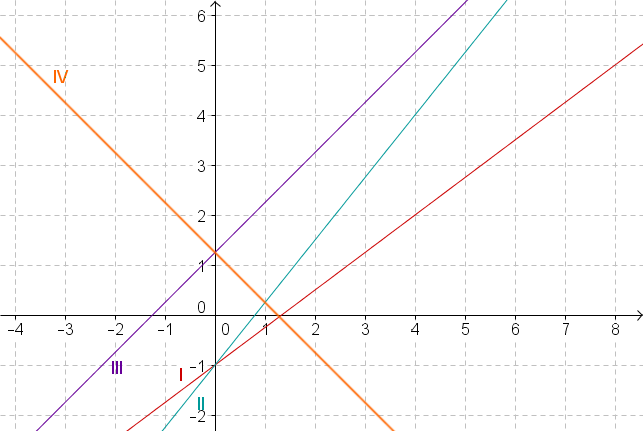
Which of the four graphs belongs to the equation ?
For this task you need the following basic knowledge: Line Equations
You are given the graph equation:
You can read the slope and the y-intercept of this graph from the equation.
First check for which functions the y-intercept is by reading the y-value of each graph by cutting the y-axis.
Only graph I and II have the y-intercept so you can exclude any other graph.
Now check which of the two graphs has the slope by going one unit to the right from the point and checking which of the two -values increases by .
Both graphs start at the point . As the straight line you are looking for has a gradient of , it also passes through the point .
Only line II runs through this point.
Graph II is the one that belongs to the given equation.
Wie lautet die Gleichung zum Graphen III?
For this task you need the following basic knowledge: Line Equations
We have to check graph III
First read where the graph intersects the y-axis to determine the y-intercept.
The y-value of the point where the y-axis is intersected is . Therefore, .
Now read off how much the y-value changes if you go one to the right starting from . This will give you the gradient.
The y-value increases from to . The gradient is therefore .
Set up the equation.
⇒ Graph III has the equation .
- 2
The following diagrams contain graphs of linear functions. Determine the function terms.
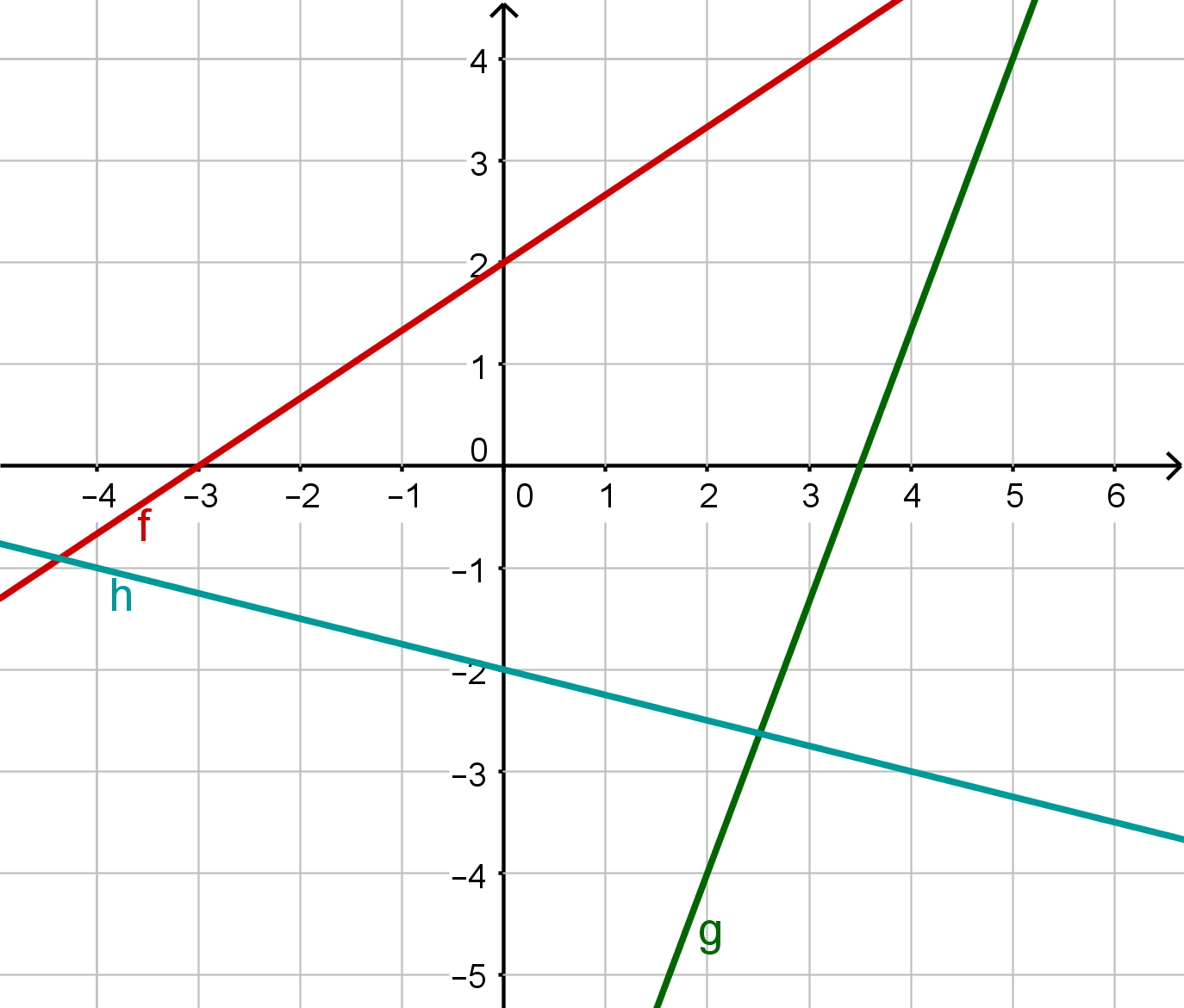
For this task you need the following basic knowledge: Linear Functions
Linear function
Set up the general form of a linear function.
Read off the y-intercept from the diagram.
Read off two points from the graph of the linear function to calculate the gradient:
You can use these points, for example:
and
and
For the gradient, you then get by substituting:
Now plug the calculated values of and into the general form:
Linear function
Set up the general form of a linear function.
Read off two points on the graph of the linear function to calculate the gradient.
For example, you can use these two points:
and
and
The gradient is then:
As the y-intercept is not visible, you have to calculate it. To do this, set up the equation of the line.
Insert one of the points, for example .
Now solve for .
Substitute the values of and into the general form of the linear function, and you will get the linear equation:
Linear function
Set up the general form of a linear function.
Read off two points from the graph of the linear function to calculate the gradient:
You can use these two points, for example:
and
and
Now use them to calculate the gradient:
Either read off or calculate the value. To calculate it, set up the linear equation.
Insert a point that lies on the straight line, for example .
Now, solve for .
Setze und in die allgemeine Form ein und du erhältst die Geradengleichung:
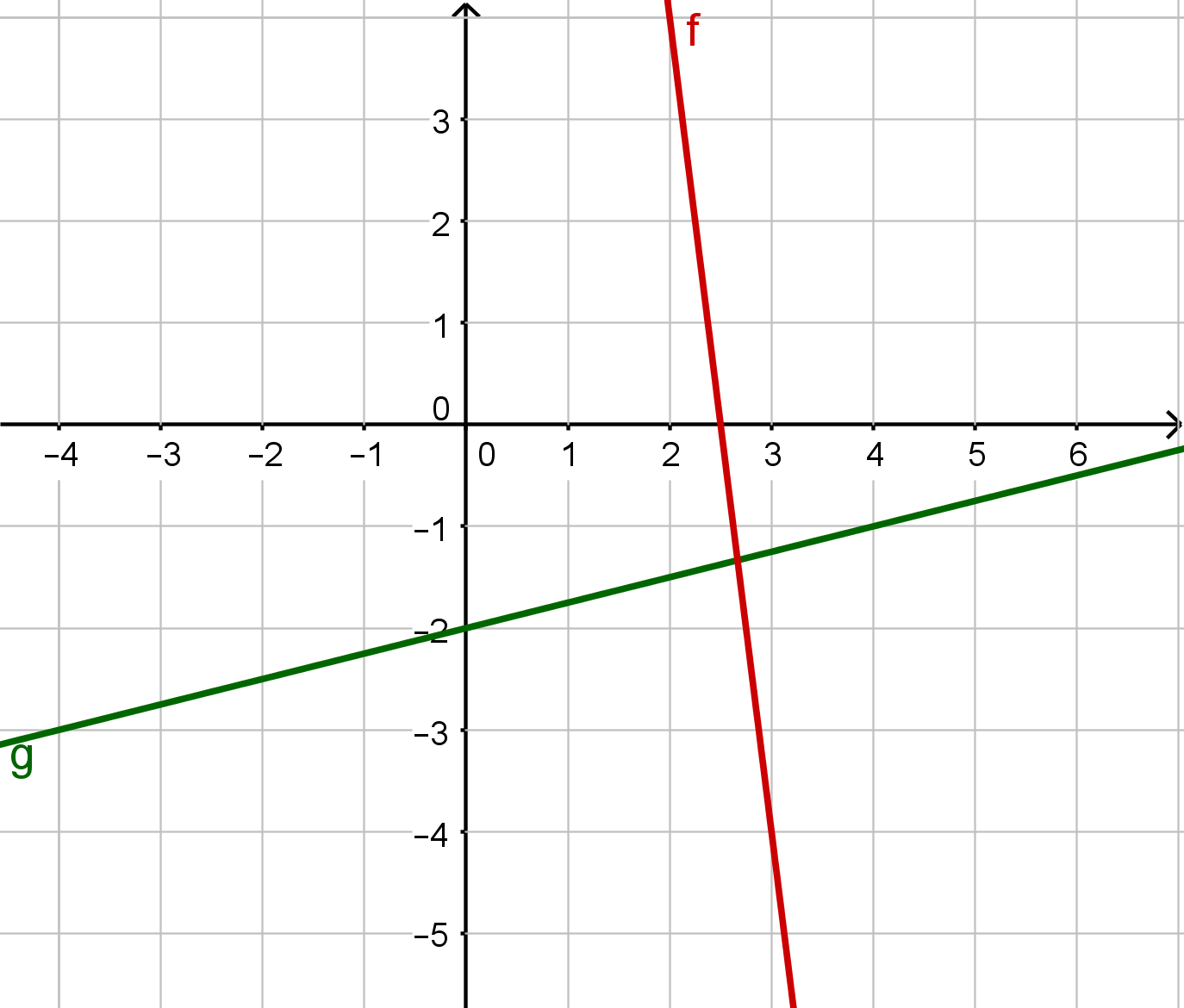
For this task you need the following basic knowledge: Linear Functions
Linear function
Set up the general form of a linear function.
Read off two points from the graph of the linear function to calculate the gradient:
You can use these two points, for example:
and
and
The result is a gradient:
As the y-intercept is not visible, you have to calculate it. Therefore, set up the equation of the line:
Insert one of the points, for example :
Solve for .
Plug and into the general form, and you will get the linear equation as a result:
Linear function
Set up the general form of a linear function.
Read off two points from the graph of the linear function to calculate the gradient:
You can use these two points, for example:
and
and
Now use them to calculate the gradient:
Read off the y-intercept from the diagram.
Plug and into the general form of the linear function, and you get the line equation of :
- 3
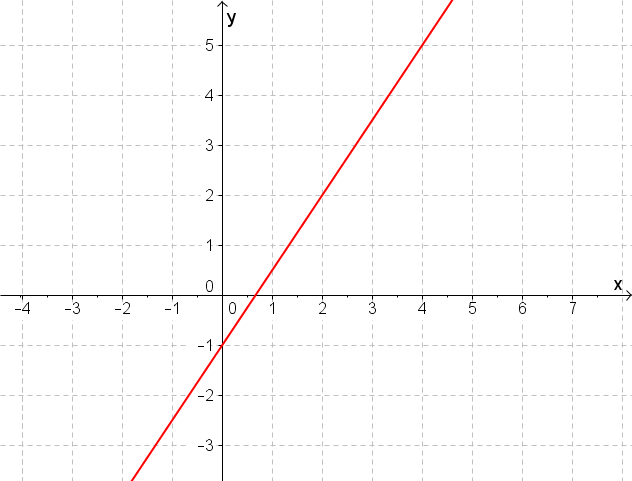
Determine the equation of the following straight line:
For this task you need the following basic knowledge: Lines in Coordinate Systems
The general line equation is:
Read the y-intercept , i.e. the point at which the straight line intersects the y-axis, from the drawing.
Find two points with (at best) integer coordinates.
and are on the line
There are two ways to determine the gradient :
1.
Plug in the coordinates of and .
2.
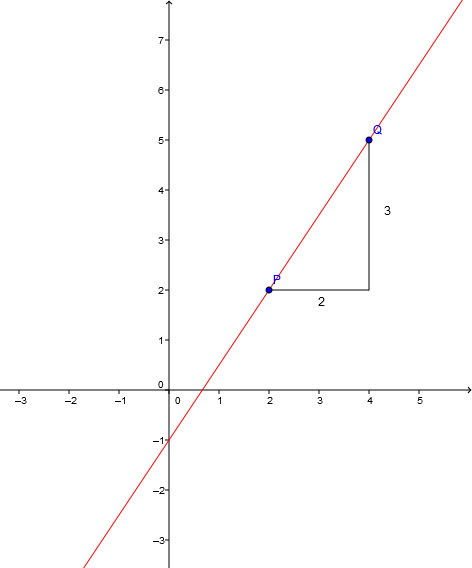
Draw a slope triangle between the points. The vertical distance is the numerator, the horizontal distance is the denominator of the fraction that describes the gradient.
The line equation is therefore given by :
- 4
Calculate the gradient of the straight line through the given points.
,
For this task you need the following basic knowledge: Slope/Gradient of a Line
Insert the points into the difference quotient for the line.
↓ Simplify numerator and denominator
The gradient of the line is .
,
For this task you need the following basic knowledge: Slope/Gradient of a Line
Insert the points into the difference quotient for the line.
↓ Simplify numerator and denominator
The gradient of the line is m = 1.
- 5
Solve the following exercises.
What is the gradient of the straight line through the points and ?
For this task you need the following basic knowledge: Line Equation
You are given the points and
Insert the x-values (first coordinate) and the y-values (second coordinate) into the general line equation.
In the first equation, you can immediately see that . You can insert this into the second equation to calculate .
Plug and into the general line equation.
Set up the equation of the line through the points and .
For this task you need the following basic knowledge: Line Equation
You are given the points and
Calculate the difference between the two x-values and the two y-values to determine the gradient.
x-values:
y-values:
While the x-value increases by 2, the y-value decreases by 4. Divide the y-value by the x-value to calculate the gradient.
Substitute m, the x-value and the y-value of one of the points into the general line equation to determine .
Plug and into the general linear equation to set up the equation of the function.
- 6
What is the gradient of the line through the points and ? What is its function equation?
For this task you need the following basic knowledge: Lineare Funktionen
Gradient
Determine the gradient .
Insert the two points into the formula for the gradient.
Function equation
Determine the function equation.
Insert m into the general line equation.
Insert one of the two points into the function equation.
Substitute t into the function equation.
- 7
Set up the equation of the straight line through the points and .
For this task you need the following basic knowledge: Linear Function
You are given the points and .
You are looking for the equation of the straight line that passes through the two points.
To determine the linear equation, it is best to first consider the general form of the linear equation:
Determination of the gradient
Firstly, recall the equation for the gradient of a straight line:
Plug the values from the points and into the formula.
Shorten the denominator.
Now you know that the equation of the line through the points and looks like this:
Next, determine the y -intercept ().
Determination of the y -intersect
To determine , insert the - and -values of one of the two points into the equation of the line. This is calculated using the point as an example
The -intercept of the function is 5. This gives you the function equation.
- 8
Set the equation of the straight line with gradient through the point and draw it in a coordinate system.
For this task you need the following basic knowledge: Linear Function
Setting up line equations
;
Plug and into the general linear equation and solve for .
↓ ↓ Reduce the two fractions to the same denominator.
↓ Subtract.
↓ Convert to a mixed fraction.
↓ Setze t und m in die allgemeine Geradengleichung ein.
Drawing the line
To determine , you substitute the - and -values of one of the two points into the equation of the line. Here, it is calculated exemplarily with the point ."
Choose any point on the line, for example, the given point . Find a second point by moving from the point 1 unit to the right. According to the slope , 1you then have to go units down. You obtain the green slope triangle. Connect the two points to form a line.
Alternatively, you can find the second point by moving 3 units to the right and 4 units down. You obtain the orange slope triangle. (The slope is still .)
- 9
Write the equation of the straight line that runs through the point and has the gradient . Draw the straight line.
For this task you need the following basic knowledge: Line Equation
1. insert and the coordinates of the point into the general line equation and solve for .
2. Plug and into the general linear equation
Drawing the line
Draw the given point in the coordinate system. Then draw a slope triangle by moving 1 unit to the right and 2 units down (). Mark the point there. Connect and to form a line.
- 10
Set up the equation of the line through the two points and draw it.
and
For this task you need the following basic knowledge: Line Equation
Determining the line equation
Determine the gradient of the general line equation using the difference quotient.
Plug and the coordinates of a point, e.g. into the general line equation and solve for .
Substitute and into the general line equation.
Drawing the line
Draw the two points und into the coordinate system and connect them to form a line.
and
For this task you need the following basic knowledge: Line Equation
Determining the line equation
Determine the gradient of the general line equation using the difference quotient.
Plug and the coordinates of a point, e.g. into the general line equation and solve for .
Substitute and into the general line equation.
Drawing the line
Draw the two points und into the coordinate system and connect them to form a line.
and
For this task you need the following basic knowledge: Line Equation
Determining the line equation
;
Determine the gradient of the general line equation using the difference quotient.
Plug and the coordinates of a point, e.g. into the general line equation and solve for .
Substitute and into the general line equation.
Drawing the line
Draw the two points und into the coordinate system and connect them to form a line.
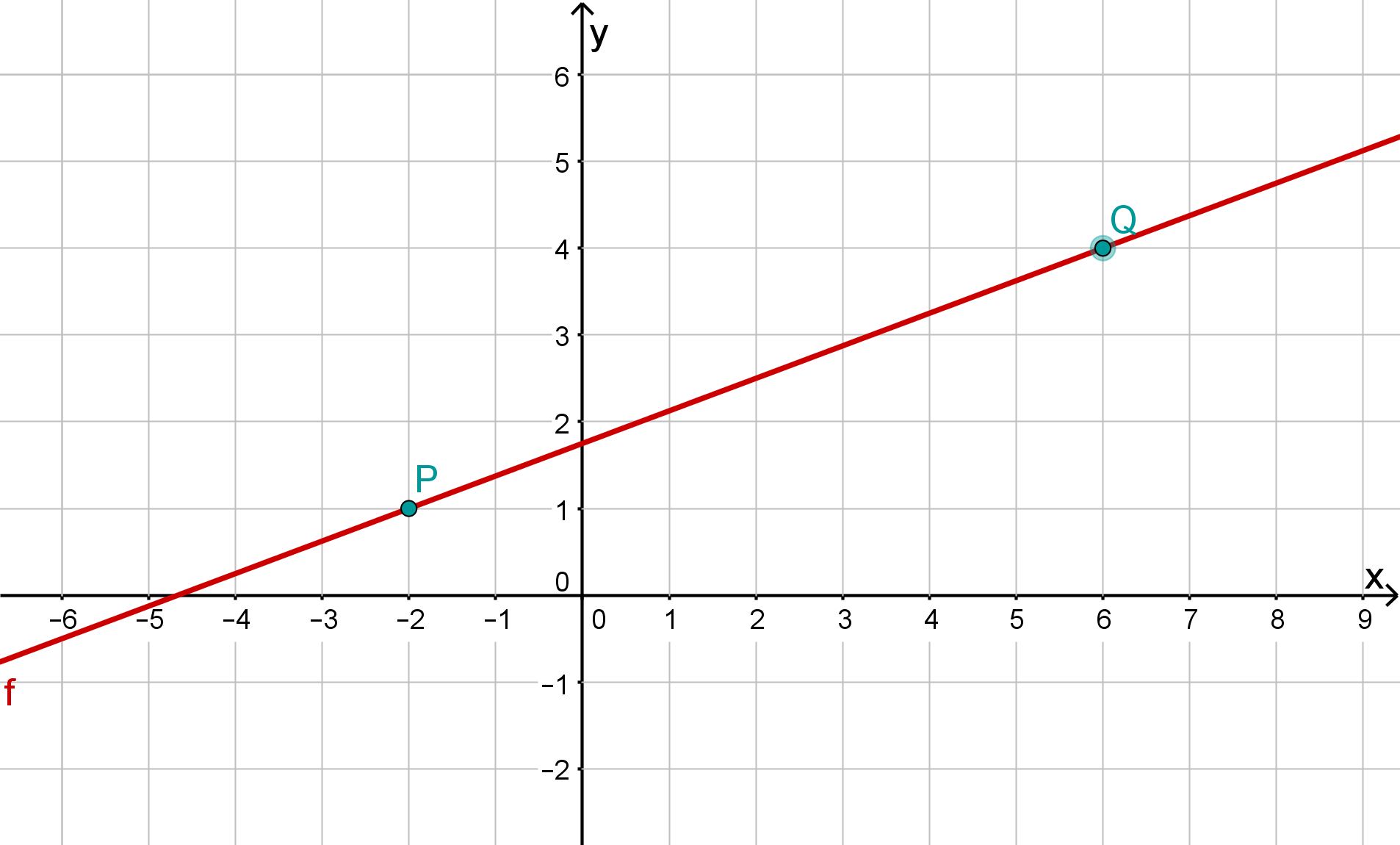
and
For this task you need the following basic knowledge: Line Equation
Determining the line equation
;
Determine the gradient of the general line equation using the difference quotient.
Plug and the coordinates of a point, e.g. into the general line equation and solve for .
Substitute and into the general line equation.
Drawing the line
Draw the two points and into the coordinate system and connect them to form a line.
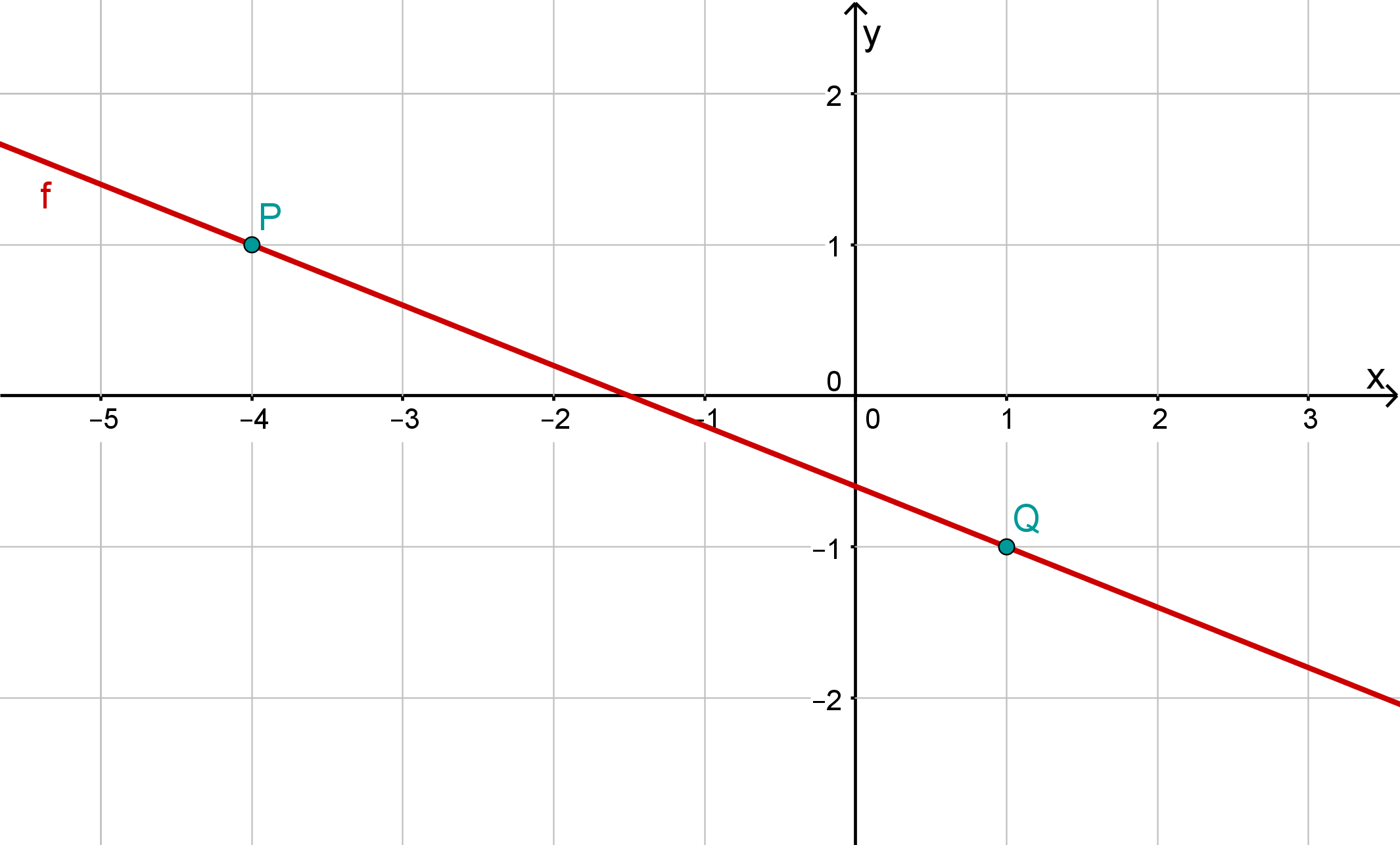
- 11
Given are the y-intercept and the point . Calculate the corresponding equation of the line and plot the line.
For this task you need the following basic knowledge: Line Equation
1. Insert and the coordinates of the point into the general equation of the line and solve for .
2. Substitute and into the general line equation
Drawing the line
Draw the given point in the coordinate system. Then, draw the point (y-intercept and connect the points and to form a line.
- 12
For a linear function , suppose we know:
and . Determine .
For this task you need the following basic knowledge: Line Equation
For a function, the y-intercept is equal to the value at .
Now use the two given points to determine the gradient using the difference quotient.
Put together the line equation.




