Setting up Quadratic Function Terms

3 Points Given

Since a quadratic function is uniquely determind in its normal form by $f(x)=ax^2+bx+c$ , after inserting three points you get a linear system of equations with three equations and the three values you are looking for, a, b and c, which you have to solve.  

General approach for 3 given points

Step 1:

Given pairs of points in the function equation

$f(x)=ax^2+bx+c$

so that you get three equations.

Step 2:

Solve the linear system.

Step 3:

State the function term.

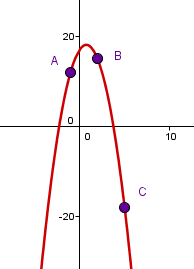
Example

We are looking for the quadratic function that passes through the points $A(-1|12)$, $B(2|15)$ and $C(5|{-}18)$.

Step 1: Insert the given pairs of points into the function equation $f(x)=ax^2+bx+c$.$\def\arraystretch{1.25} \begin{array}{llrcl}A(-1|12): &I &12 &= &a\cdot (-1)^2+b\cdot (-1)+c\\B(2|15): &II &15 &= &a\cdot 2^2+b\cdot 2+c\\C(5|{-}18): &III &-18 &= &a\cdot 5^2+b\cdot 5+c\end{array}$

Step 2: Solve the linear system.

For instance, you could use the addition method.

Detailed calculation, here with addition method

$\def\arraystretch{1.25} \begin{array}{llrcl}A(-1|12): &I &12 &= &a\cdot (-1)^2+b\cdot (-1)+c\\B(2|15): &II &15 &= &a\cdot 2^2+b\cdot 2+c\\C(5|{-}18): &III &-18 &= &a\cdot 5^2+b\cdot 5+c\end{array}$

First you need to multiply the numbers on the right-hand side.

$\def\arraystretch{1.25} \begin{array}{llrcl}&I' &12 &= &a &-b &+c\\&II' &15 &= &4\cdot a &+2\cdot b &+c\\&III' &-18 &= &25\cdot a &+5\cdot b &+c \end{array}$

You will notice that all three equations have the term $+c$ at the end. You can therefore get rid of this by subtracting one equation from another. For example, by subtracting $II′$ from $I′$ you get:

This equation can easily be solved for $b$. The following applies:

$3-3a=3b$, or simply

Even if you subtract equation $III'$ from $II'$ , the $c$ will vanish. Then you get:

If you plug in the solution $1 - a = b$ from above, you obtain

$33=-21a-3\cdot(1-a)$,

and the equation can be summarised as

If you add $3$ on both sides, you get

$36=-18a.$

Dividing by $-18$ on both sides yields:

Since $1-a = b$ was already known, you can use $a = -2$ here and you get

Now you can insert both values of $a$ and $b$ in $III'$ , which renders:

This equation is first multiplied out and then summarised:

$-18=-35+c$

So, after adding 35 on both sides,

The result is therefore $a=-2, b=3, c=17$.

Step 3: State the function term: $f\left(x\right)=-2x^2+3x+17$ .

Vertex and another point given

If you are given a vertex and another point, it is advisable to set up the vertex form and then calculate the missing parameter $a$ using the given point. To obtain the function in the form $f(x)=ax^2+bx+c$, you now need to multiply out.

General procedure for given vertex and given point

Step 1:

Use the vertex to set up the vertex form.

Step 2:

Calculate the missing parameter $a$ by inserting the given point into the vertex form and solving for the parameter.

Step 3:

State the function term.

Hint

The vertex can also be given indirectly by describing the function with shifts. "The parabola is shifted 3 to the right and 2 upwards" means, for example, that the vertex is at (3|2).

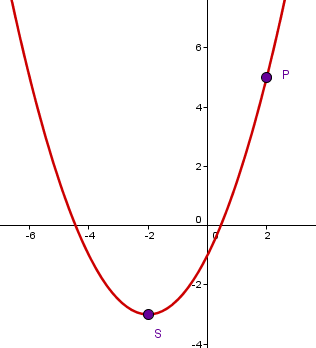
Example

We are looking for the quadratic function f with vertex $S(-2|-3)$, running through the point $P(2|5)$ .

Step 1: Use vertex S to set up the vertex form: $f(x)=a\cdot(x+2)²\;-3$.

Step 2: Calculate the missing parameter $a$ by plugging the given point P into the vertex form and solving for $a$:$\def\arraystretch{1.25} \begin{aligned}5 &= a(2+2)^2-3\\\Rightarrow 8 &= 16a\\\Rightarrow a &= \frac 12\end{aligned}$

Step 3:

The quadratic function is therefore $f(x)=\frac12(x+2)^2-3$, or multiplied out: $f(x)=\frac12x^2+2x-1$.

Download original Geogebra file

Points and additional information given

Additional information is often given in the exercise setting, which can then be used to specify the function term. However, a single piece of additional information is often not enough to specify the entire function term.

Examples of additional information

• "Normal parabola": The pre-factor $a$ is equal to 1 (if the parabola is open upwards) or equal to -1 (parabola open downwards).

• "Parabola opening upwards" or "parabola opening downwards": Positive or negative sign of the pre-factor $a$ (see parabola ).

• "assumes only positive / negative values": Parabola always runs above or below the x-axis. So the y-coordinate of the vertex is greater / less than 0.

• "same y-coordinate at two given points": The vertex lies exactly between the two given points with respect to the x-coordinate (symmetry of parabolas).

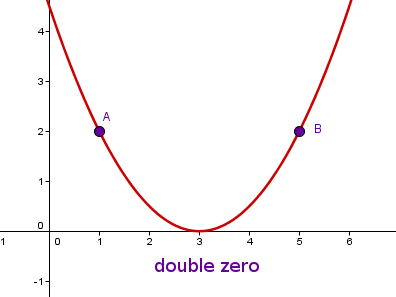
• "Double zero": If a parabola has a double zero, then this zero is at the same time the vertex. It therefore lies on the x-axis and thus has y -coordinate 0.

Example

We are looking for a parabola that has a double zero and passes through the points $A(1∣2)$ and $B(5∣2)$. In this case, the additional information is "double zero". This means that the vertex lies on the x-axis. In addition, the two points have the same y-coordinate, i.e. the vertex lies exactly between them. Together, this results in the vertex $S\left(3\vert\;0\right)$. Now you can solve a linear system of equations with the three points or set up the vertex form with the vertex and insert another point. So you first get $f(x)=a\cdot\left(x-3\right)^2+0$ and insert the point $B$, for example, to get $a=\frac12$.

So the overall result is $f\left(x\right)=\frac12\left(x-3\right)^2=\frac12x^2-3x+\frac92$

Download original Geogebra file

Parabola given as function graph

If the parabola is given as a function graph in the coordinate system, you can read off the function equation in two ways:

Read off three points

You can read favourably located points from the coordinate system in order to apply the known solution approaches. Practical points are the vertex and the zeros.

Directly reading off the vertex

You can also read off the equation directly. To do this, use the vertex form  $y= a\left( x- d\right)^2+ e$ .

• The coefficients $d$ and $e$ are the coordinates of the vertex  $\mathrm S\left( d\left| e\right.\right)$

• The coefficient $a$ can be read off by moving one unit to the right or left from the vertex and reading off how far upwards (if $a$ is positive) or downwards (if $a$ is negative) you have to go.

Example

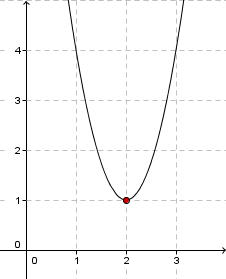
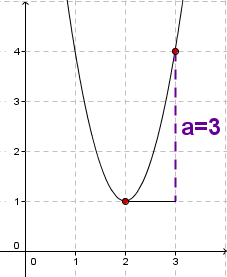
The vertex is at (2|1), so you get

$\boldsymbol y\boldsymbol=\boldsymbol a\left(\boldsymbol x\boldsymbol-\mathbf2\right)^\mathbf2\boldsymbol+\mathbf1$

If you go one unit to the right from the vertex, you have to go up by three units until you are back on the graph. So the function term is

$\boldsymbol y\boldsymbol=\mathbf3\left(\boldsymbol x\boldsymbol-\mathbf2\right)^\mathbf2\boldsymbol+\mathbf1$