Parabola
A parabola is the graph of a quadratic function.
Parabolas have a typical arc-shaped appearance and can be open upwards or downwards. Their uniquely determined lowest or highest point is called the vertex. A parabola is called a normal parabola if its function equation is
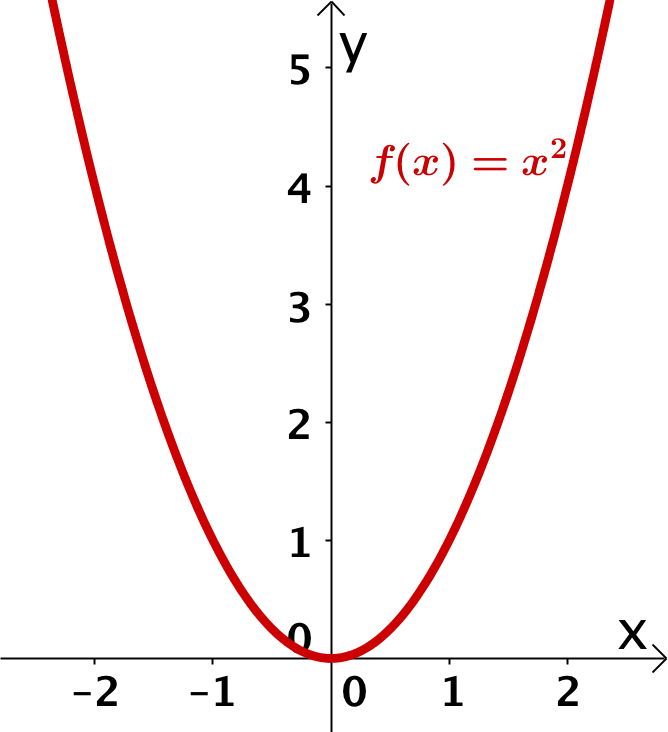
Normal Parabola
The normal parabola is the function graph of the function
It has the following features:
Vertex at
open upwards
axisymmetric to the y-axis
passes through the points
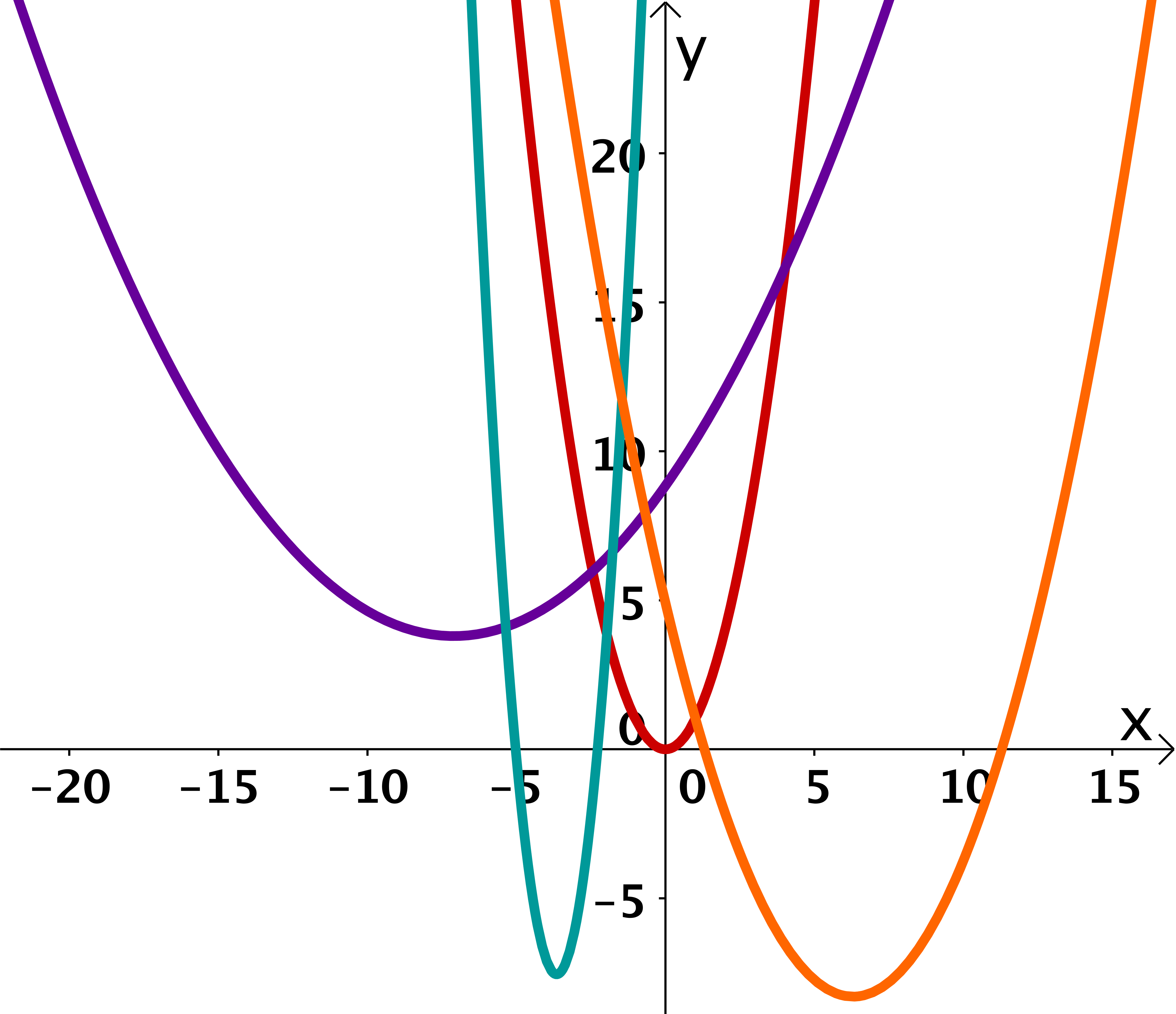
General Parabola
Starting from the normal parabola, one can construct any parabola. To do this, use the vertex form:
The relationship between the parameters in the vertex form and the graph can be found in the corresponding article. This allows the construction of various parabolas, as can be seen in the graph on the right.
Video of the Apex
Loading
Draw Parabola in the coodrinate system
You can draw parabolas using a table of values or using a parabola template and the deformation rules.
Alternative definition of a parabola
A parabola consists of those points which are equidistant from a given straight line and a given point (focal point).
Illustration on the Applet
Parables in everyday life
Parables are often found in everyday life:
Water jets, such as in drinking fountains, describe parabolas.
If you throw a ball horizontally, you get a throwing parabola.
In parabolic flights, the flight path of the aircraft runs along a parabola. Parabolic flights are used to simulate different gravity situations.
The name parabolic antenna is derived from the parabolic cross-section. (Parabolas are generally called lines that have a focal point, which is used here to bundle and thus amplify beams, such as in satellite dishes).
Parabolic arcs are also often found under bridges, as they are more stable compared to circular arcs, for example.
On the other hand, power lines hanging between two poles do not form a parabola, but a so-called catenary, which only looks very similar to the parabola.
