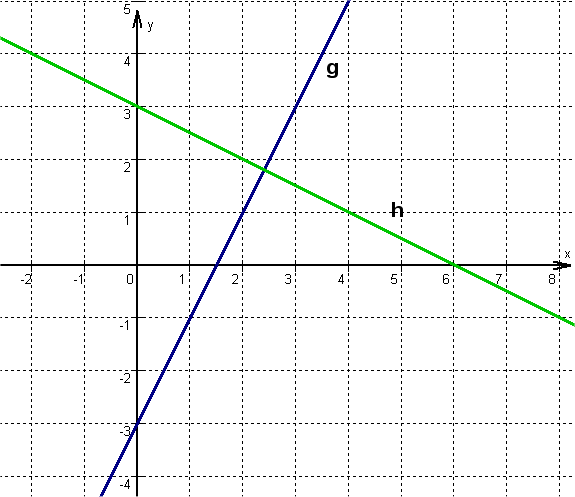
For this task you need the following basic knowledge: Line equation
Part 1
Drawing a sketch
Select any point on the straight line, e.g. the -axis intercepts and . Go from there 1 unit to the right and, corresponding to the slopes, upwards and downwards. Connect the two points to form a straight line.
If you look at the straight line and, for example, the position of point , you will see that it will hardly lie on the straight line , but probably on . Similarly, you can decide for other points whether a mathematical check is worthwhile: Point can only lie on , for example.
Check by computation
Put the coordinates of the points into the equation in question. So set and .
Check if the equation is a true statement.
does not lie on any of the straight lines. This can be clearly seen in the sketch.
is plugged into : This statement is false, so does not lie on .
is plugged into : This statement is false, so does not lie on .
is plugged into : This statement is true, so lies on .
Part 2
Completing coordinates
The given coordinate of the point (the -coordinate) is inserted into the function equation and the missing -coordinate is calculated from it.
Q:
R:
S:
Part 3
Proof for
Insert the coordinates of into both line equations. If the statements are true, lies on the lines.
Both equations give correct statements, so the point lies on both straight lines.
Is the intersection point of the lines.