Exercises: Square Roots

Heron's Method

Heron's method is an algorithm that allows you to estimate the value of square roots.

You try to find a square whose area is the number under the root (which is $7$, here). The side length is then the square (which is $\sqrt{7}$, here).

To find the square, you start with a rectangle of area $A=7$ and change its shape to be more "square-like" step by step.

Step 1

Find the first rectangle by picking two side lengths $a$ and $b$, such that the area of the rectangle is

$A=a\cdot b$

In our case, $A=7$ so it follows to choose

$a_0=7$

$b_0=1$

In the figure below you can see the initial rectangle.

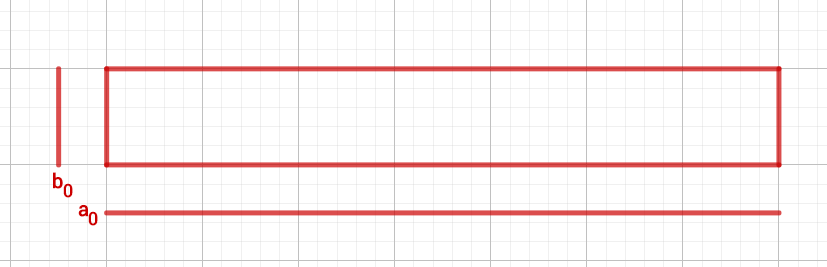
The next steps always follow the same pattern:

• First you calculate the mean value of the old side lengths, which will be one of your new side lengths, called $a$.

• Then you calculate the other side length $b$ by dividing $\frac{A}{a}$ with $A$ being the fixed area.

You can find a detailed explanation of these steps in this applet.

Step 2

Calculate the mean value of $a_0$ and $b_0$.

$a_1={\displaystyle \frac{a_0+b_0}{2}}={\displaystyle \frac{7+1}{2}}=4$

Then calculate $b_1$.

$b_1={\displaystyle \frac{A}{a_1}}={\displaystyle \frac{\text{radicand}}{a_1}}={\displaystyle \frac{7}{4}}=1.75$

Your new side lengths are

$a_1=4$

$b_1=1.75$

In the figure below you can see the original rectangle (red) and the new one (blue), which has now become a bit more square-like.

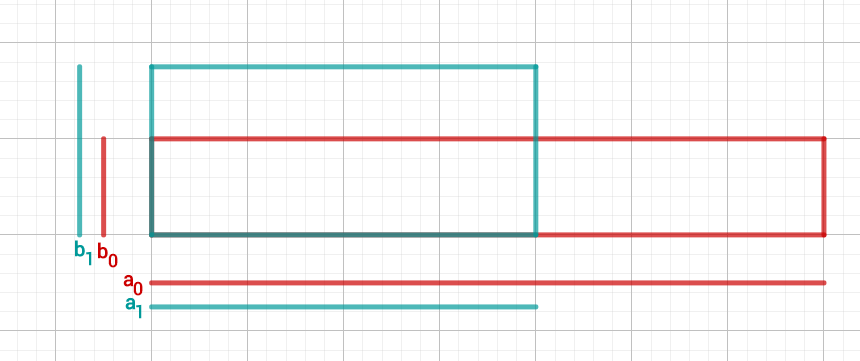
Step 3

Calculate the mean value of $a_1$ and $b_1$.

$a_2={\displaystyle \frac{a_1+b_1}{2}}={\displaystyle \frac{4+1.75}{2}}=2.875$

Then calculate $b_2$.

$\begin{array}{l}{b}_2={\displaystyle \frac{A}{a_2}}={\displaystyle \frac{\text{radicand}}{a_2}}\\ ={\displaystyle \frac{7}{2.875}}=2.4348\end{array}$

Your new side lengths are

In the figure below you can see the new rectangle in orange.

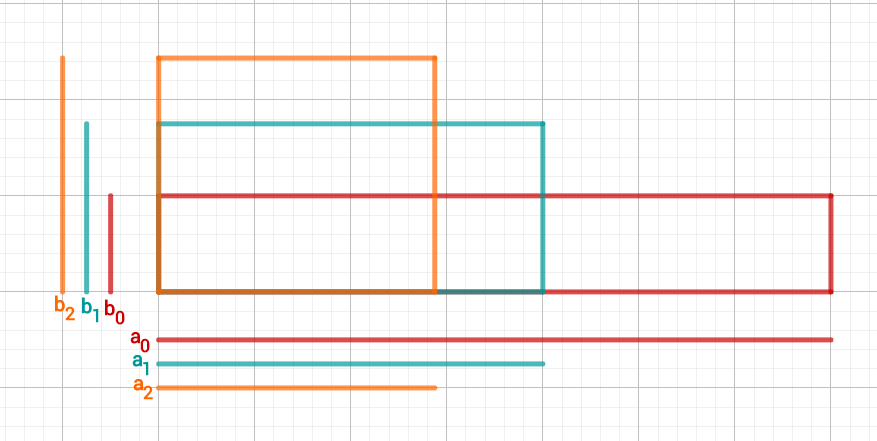
Step 4

Calculate the mean value of $a_2$ and $b_2$.

$a_3={\displaystyle \frac{a_2+b_2}{2}}={\displaystyle \frac{2.875+2.4348}{2}}=2.6548$

Then calculate $b_3$.

$\begin{array}{l}{b}_3={\displaystyle \frac{A}{a_3}}={\displaystyle \frac{\text{radicand}}{a_3}}\\ ={\displaystyle \frac{7}{2.6548}}=2.6367\end{array}$

Your new side lengths are $a_3=2.6548$ and $b_3=2.6367$.

You may notice these two values are not that different anymore.

In the figurebelow you can see the change in the rectangles. The last one (purple) is already almost a square.

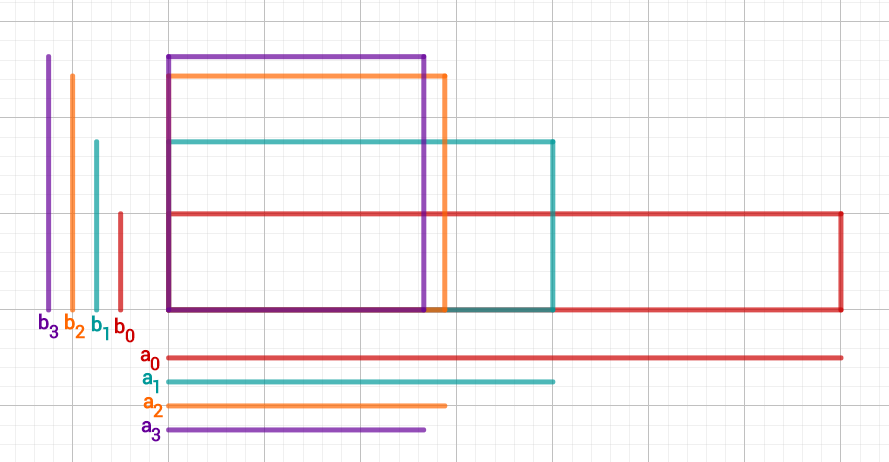
Final Estimate

You could do as many further steps as you wish in order to get a more precise result. Now, the problem setting tells us to do exactly four steps, so we will stop here.

Since $a_3=2.6548$ and $b_3=2.6367$, the value of $\sqrt{7}$ must be between these two numbers. So a good estimate for $\sqrt{7}$ is given by the mean value of the two numbers:

For comparison: The precise value of $\sqrt{7}$ is $2.64575\dots$