Exercises: Square Roots
Here you will find mixed problems with root terms, as well as equations that are solved using the square root. Can you do them all?
- 1
Solve the following equations.
- 2
Which of the following roots are well-defined (i.e., they exist)?
- 3
Which of the following roots are well-defined (i.e., they exist)?
- 4
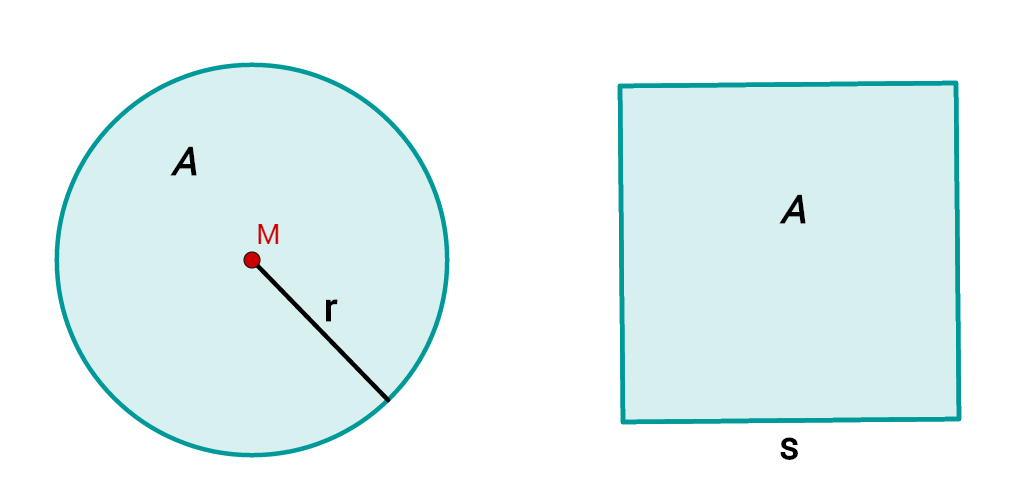
A square and a circle have the same area.
The radius of the circle is . What is the side length of the square?
- 5
Estimate the value of .
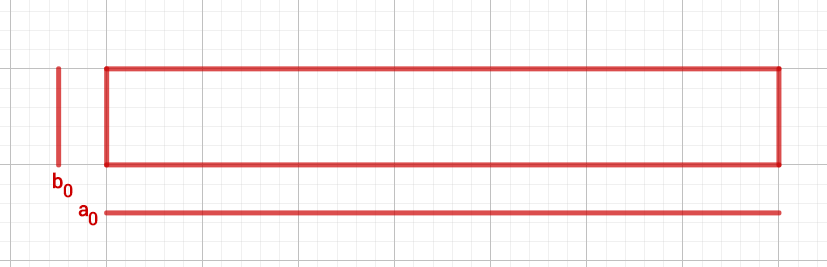
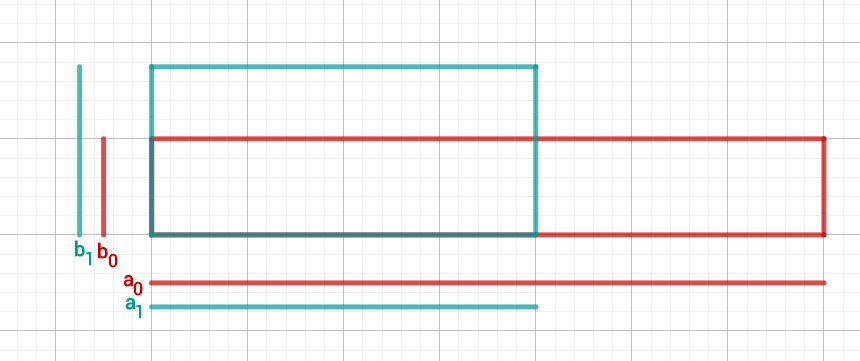
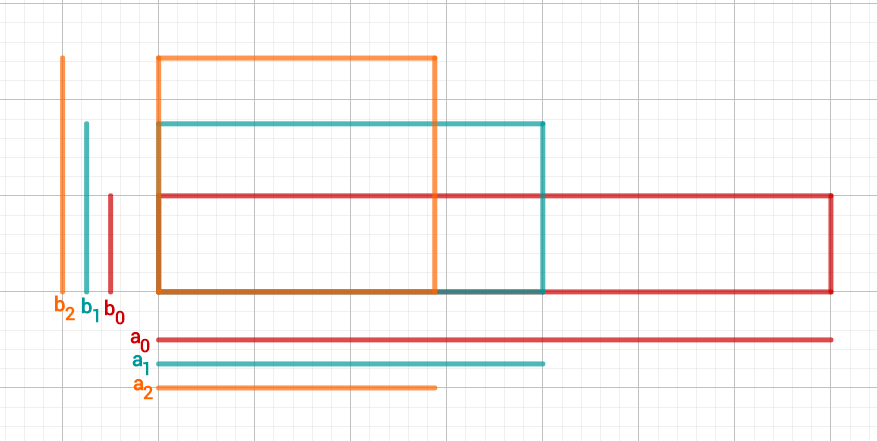
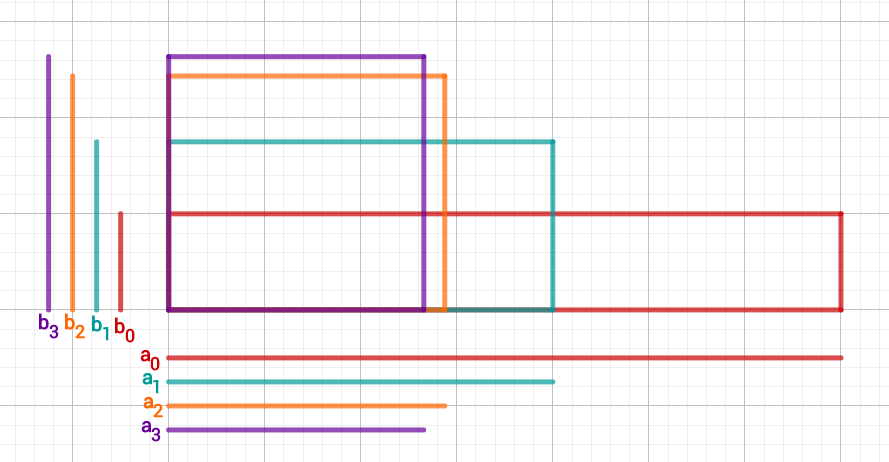
Calculate the first five steps of the interval nesting and then estimate the value of .
- 6
Estimate the value of .
Calculate the first four steps using Heron's method and then estimate the value of .
- 7
Simplify these root terms as far as possible.
- 8
Which are the two natural numbers between which lies?
- 9
The orange square and the purple rectangle have the same area. The purple rectangle has side lengths b and c. The side length b is 2cm long and the side length c is 8cm long. Calculate the side length a of the square.
- 10
Tina wants to build a cat out of square tiles. She uses a template with rows and columns. The complete picture of the cat should be in size. Tina thinks about how big the tiles have to be. Can you help Tina calculating the side length of the tiles?
- 11
Estimate the value of both and by replacing them with simpler values.
- 12
Suppose, you have forgotten your calculator and need the result of. Can you give a good estimate? For instance, between which integers lies?
- 13
In the following table the side length of a square or its area is given.
Some values are still missing in the tables. Calculate them without a pocket calculator.
a
?
?
?
?
a
?
?
?
?
- 14
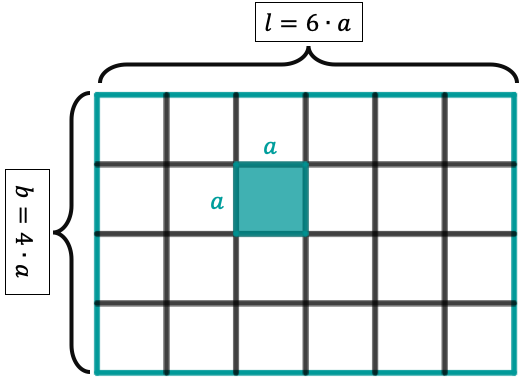
The square marked in colour has an area of . Determine the perimeter of the rectangle.
- 15
Sara and her older brother Markus have a conversation after school. Markus makes his little sister think. Can you help Sara solve the problem?