Exercises: Power- and root functions
Bestimme den Grad folgender Potenzfunktionen, mache eine Aussage über das Symmetrieverhalten, den Verlauf des Graphen und die Wertemenge. Zeichne die Graphen jeweils in ein Koordinatensystem.
For this task you need the following basic knowledge: Potenzfunktion
Lies den Grad der Potenzfunktion ab.
Setz in ein, um die Symmetrie des Graphen zu ermitteln.
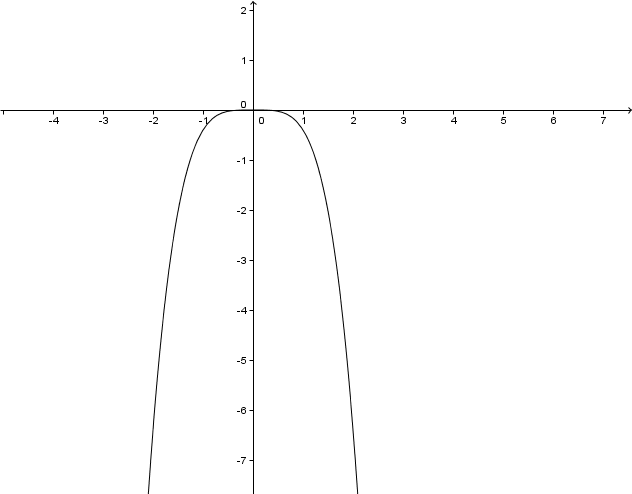
Der Graph ist achsensymmetrisch .
Setz einen Wert über 0 und einen unter 0 ein, um den Verlauf des Graphen zu ermitteln.
Der Graph verläuft durch den III und IV Quadranten .
Bestimme die Wertemenge, indem du überprüfst, welche Werte für f(x) möglich sind.
Es gibt keine Definitionslücke. Das Ergebnis der Funktion kann aber nur negativ sein, weil vor dem eine negative Zahl steht.
Zeichne den Graphen. Rechne dazu einige Werte der Funktion aus.
For this task you need the following basic knowledge: Potenzfunktionen
Lies den Grad der Potenfzunktion ab.
Setz in ein , um die Symmetrie des Graphen zu überprüfen.
Der Graph ist punktsymmetrisch .
Überprüfe den Verlauf des Graphen, indem du einen Wert unter 0 und einen über 0 einsetzt.
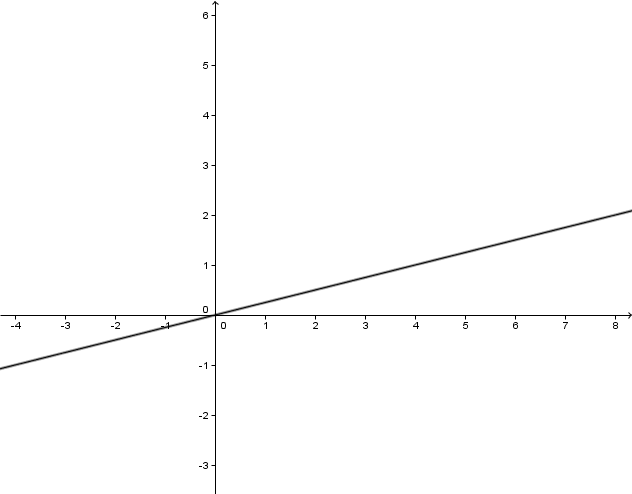
Der Graph verläuft durch den III und I Quadranten .
Bestimme die Wertemenge, indem du überprüfst welche Werte für f(x) möglich sind.
Die Funktion hat keine Definitionslücke. Es sind positive und negative Werte für f(x) möglich. Das heißt f(x) kann jeden Wert als Ergebnis haben.
Zeichne den Graphen. Rechne dazu einige Werte der Funktion aus.
For this task you need the following basic knowledge: Potenzfunktion
Lies den Grad der Potenzfunktion ab.
Setz in ein, um die Symmetrie des Graphen zu überprüfen.
Der Graph der Funktion ist achsensymmetrisch .
Bestimme den Verlauf der Funktion, indem du einen Wert unter 0 und einen über 0 einsetzt.
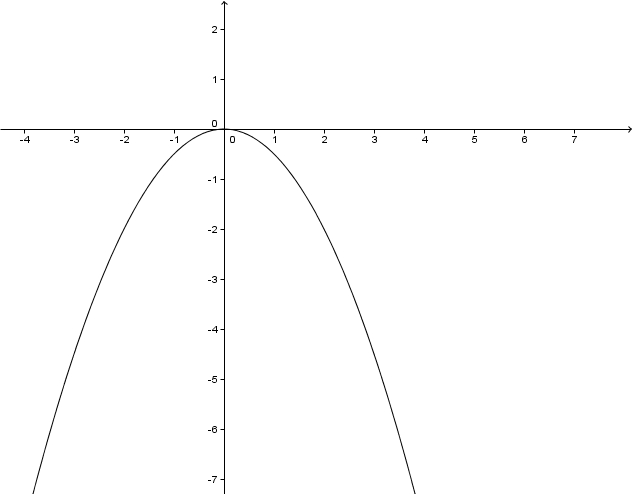
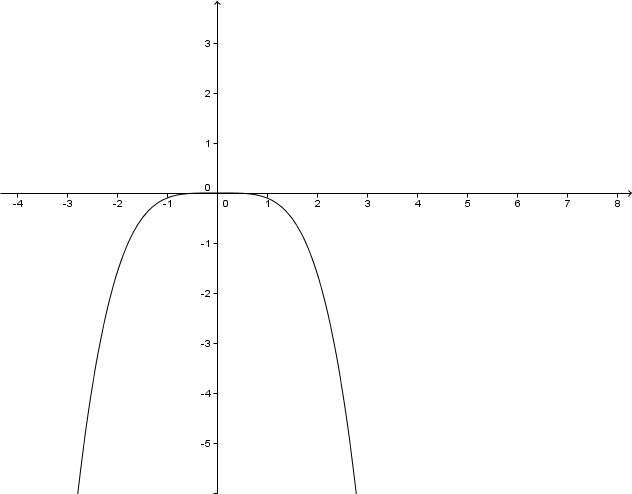
Der Graph verläuft durch den III und IV Quadranten .
Bestimme die Wertemenge, indem du überprüfst welche Werte für f(x) möglich sind.
Es gibt keine Definitionslücke. Das Ergebnis der Funktion kann aber nur negativ sein, weil bei immer positive Werte entstehen, davor aber steht.
Zeiche den Graphen. Rechne dazu einige Werte der Funktion aus.
For this task you need the following basic knowledge: Potenzfunktion
Lies den Grad der Potenzfunktion ab.
Setz in ein, um die Symmetrie des Graphen zu überprüfen.
Der Graph ist punktsymmetrisch .
Bestimme den Verlauf der Funktion, indem du einen Wert unter 0 und einen über 0 einsetzt.
Der Graph verläuft durch den III und I Quadranten .
Bestimme die Wertemenge, indem du überprüfst welche Werte für f(x) möglich sind.
Es gibt keine Definitionslücke . Das Ergebnis schließt jeden positiven und negativen Wert mit ein.
Zeichne den Graphen. Rechne dazu einige Werte der Funktion aus.
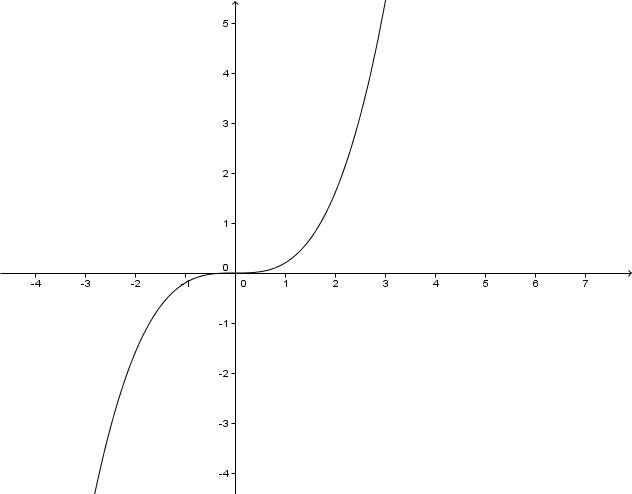
For this task you need the following basic knowledge: Potenzfunktion
Lies den Grad der Potenzfunktion ab.
Setz für ein, um die Symmetrie des Graphen zu überprüfen.
Der Graph ist punktsymmetrisch .
Bestimme den Verlauf der Funktion, indem du einen Wert unter 0 und einen über 0 einsetzt.
Der Graph verläuft durch den III und IV Quadranten.
Bestimme die Wertemenge, indem du überprüfst welche Werte für f(x) möglich sind.
Es gibt keine Definitionslücke Das Ergebnis der Funktion schließt jeden positiven und negativen Wert mit ein.
Zeichne den Graphen. Rechne dazu einige Werte der Funktion aus.
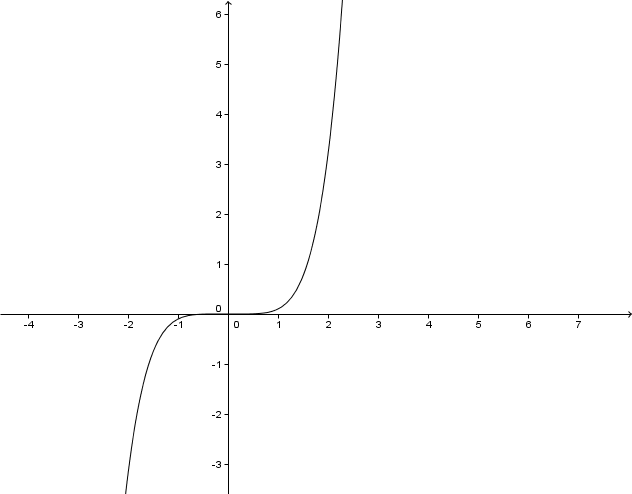
For this task you need the following basic knowledge: Potenzfunktion
Lies den Grad der Potenzfunktion ab.
Setz in ein, um die Symmetrie des Graphen zu überprüfen.
Der Graph ist punktsymmetrisch .
Bestimme den Verlauf der Funktion, indem du einen Wert unter 0 und einen über 0 einsetzt.
Der Graph verläuft durch den II und IV Quadranten .
Bestimme die Wertemenge , indem du überprüfst welche Werte für f(x) möglich sind.
Es gibt keine Definitionslücke . Das Ergebnis der Funktion schließt jeden positiven und negativen Wert mit ein.
Zeichne den Graphen. Rechne dazu einige Werte der Funktion aus.
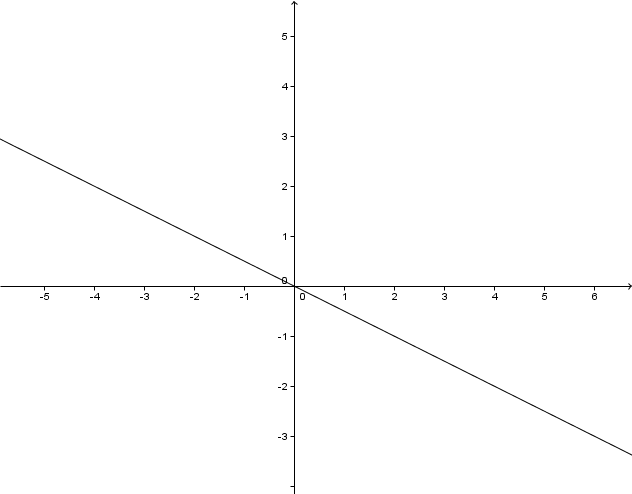
For this task you need the following basic knowledge: Potenzfunktion
Lies den Grad der Potenzfunktion ab.
Setz in ein, um die Symmetrie des Graphen zu überprüfen.
Der Graph ist punktsymmetrisch .
Bestimme den Verlauf der Funktion, indem du einen Wert unter 0 und einen über 0 einsetzt.
Der Graph verläuft durch den II und IV Quadranten .
Bestimme die Wertemenge der Funktion, indem du überprüfst welche Werte für f(x) möglich sind.
Es gibt keine Definitionslücke .Das Ergebnis der Funktion schließt jeden positiven und negativen Wert mit ein.
Zeichne den Graphen. Rechne dazu einige Werte der Funktion aus.
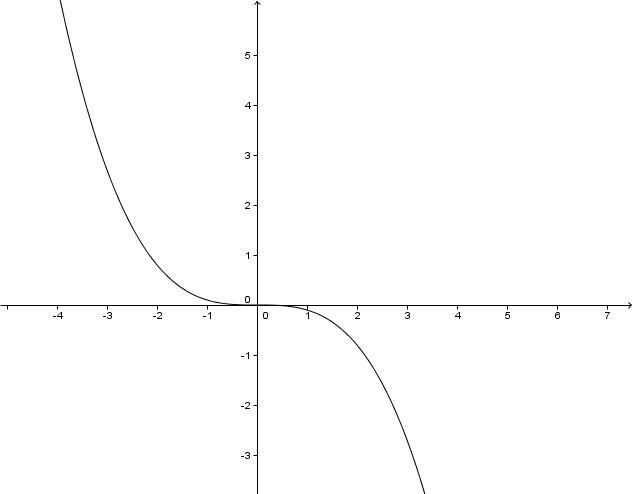
For this task you need the following basic knowledge: Potenzfunktion
Lies den Grad der Potenzfunktion ab.
Setz in ein, um die Symmetrie des Graphen zu überprüfen.
Der Graph ist achsensymmetrisch .
Bestimme den Verlauf der Funktion, indem du einen Wert unter 0 und einen über 0 einsetzt.
Der Graph verläuft durch den II und I Quadranten .
Bestimme die Wertemenge , indem du überprüfst welche Werte für f(x) möglich sind.
Der Graph hat keine Definitionslücke . Aufgrund des , das vorkommt sind aber nur positive Werte als Ergebnis möglich.
Zeichne den Graphen. Rechne dazu einige Werte der Funktion aus.
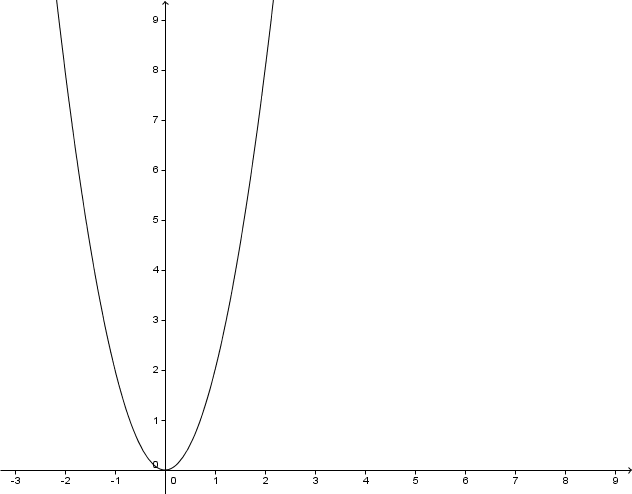
For this task you need the following basic knowledge: Potenzfunktion
Lies den Grad der Potenzfunktion ab.
Setz in ein, um die Symmetrie des Graphen zu überprüfen.
Der Graph ist achsensymmetrisch .
Bestimme den Verlauf der Funktion, indem du einen Wert unter 0 und einen über 0 einsetzt.
Der Graph verläuft durch den II und I Quadranten .
Bestimme die Wertemenge , indem du überprüfst welche Werte für f(x) möglich sind.
Der Graph hat keine Definitionslücke. Aufgrund des . das vorkommt sind aber nur positive Werte als Ergebnis möglich.
Zeichne den Graphen. Rechne dazu einige Werte der Funktion aus.
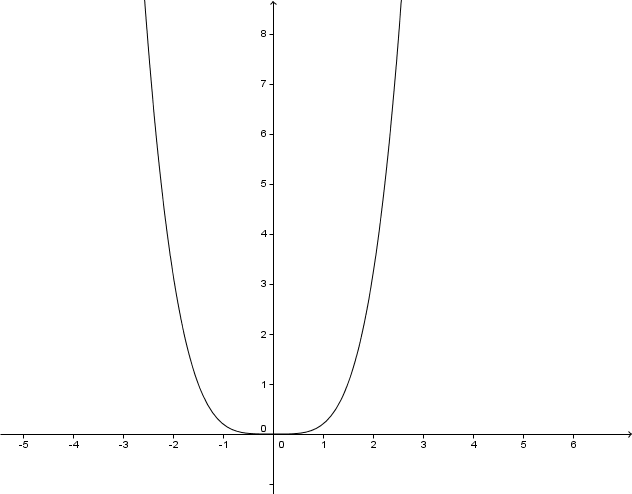
For this task you need the following basic knowledge: Potenzfunktion
Lies den Grad der Potenzfunktion ab.
Setz in ein, um die Symmetrie des Graphen zu überprüfen.
Der Graph ist achsensymmetrisch .
Bestimme den Verlauf der Funktion, indem du einen Wert unter 0 und einen über 0 einsetzt.
Der Graph verläuft durch den III und IV Quadranten .
Bestimme die Wertemenge , indem du überprüfst welche Werte für f(x) möglich sind.
Der Graph hat keine Definitionslücke . Aufgrund der negativen Zahl vor dem , sind nur negative Ergebnisse möglich,.
Zeichne den Graphen. Rechne dazu einige Werte der Funktion aus..