Exercises: Power- and root functions

- 1
Betrachte die Graphen der Potenzfunktionen im . Quadranten. Für - Werte zwischen und liegt der Graph einer Potenzfunktion höheren Grades unterhalb des Graphen einer Potenzfunktion niederen Grades. Für ist das genau umgekehrt.
Begründe dieses Verhalten.
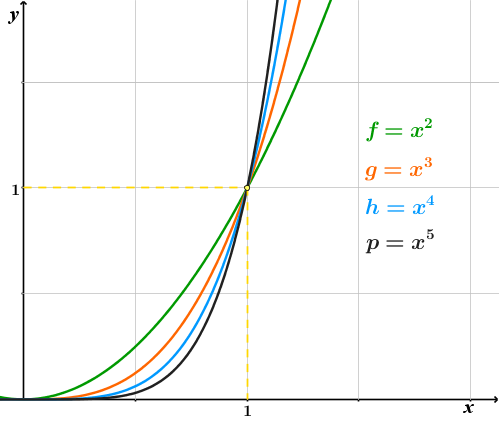
For this task you need the following basic knowledge: Potenzfunktionen
x-Werte zwischen 0 und 1
Die -Werte liegen im Bereich:
Wenn man zwei gleiche Zahlen, die zwischen und liegen, miteinander multipliziert, ist das Ergebnis kleiner als der Wert der zwei gleichen Zahlen. Wenn man das Produkt der zwei Zahlen wieder ein oder mehrmals mit dem gleichen Wert wie dem der anfänglichen zwei Zahlen multipliziert, nimmt das Ergebnis immer mehr ab. Deshalb liegen Funktionen mit größerem Exponenten im Bereich .
Vergleiche die Funktionen und .
Setze für die Zahl ein.
Setze die Zahlt für in die Funktion ein.
ist tatsächlich kleiner als . Somit liegt oberhalb von .
x-Werte größer 1
Wenn man zwei gleiche Zahlen, die größer als sind, miteinander multipliziert, ist das Ergebnis größer als der Wert der zwei gleichen Zahlen. Wenn man das Produkt wieder ein oder mehrmals mit dem gleichen Wert wie dem der zwei anfänglichen Zahlen multipliziert, nimmt das Ergebnis immer mehr zu. Deshalb liegen Funktionen mit größerem Exponenten im Bereich über Funktionen mit kleinerem Exponenten.
Vergleiche die Funktionen und .
Setze für die Zahl ein.
Setze die Zahl für in die Funktion ein.
ist tatsächlich größer als . Somit liegt oberhalb von .
- 2
Der Graph der Potenzfunktion 3.Grades soll um 2 Einheiten nach links und anschließend um 3 Einheiten nach oben verschoben werden. Gib die Funktionsgleichung für den verschobenen Graphen an.
For this task you need the following basic knowledge: Graphen verschieben
Ausgangsfunktion:
Um den Graph 2 nach links zu verschieben muss zum x-Wert 2 addiert werden und das Ergebnis dann hoch 3 genommen werden. Dies ist deshalb so, da der y-Wert beim x-Wert -2 den selben Wert haben muss wie die Ausgansfunktion beim x-Wert 0.
Nun muss der Graph noch um 3 nach oben verschoben werden. Dies entspricht dem y-Achsenabschnitt . Das heißt zum Ergebnis des vorherigen Schritt muss noch 3 addiert werden damit sich der y-Wert um 3 vergrößert.
- 3
Bestimme die Symmetrie und den Verlauf der Graphen folgender Potenzfunktionen und gib jeweils die Wertemenge und den Grad an.
For this task you need the following basic knowledge: Potenzfunktion
Somit ist der Graph punktsymmetrisch .
Verlauf des Graphen
Überprüfe durch welche Quadranten der Graph verläuft indem du einen x-Wert der kleiner als 0 und einen der größer als 0 ist, einsetzt.
Der Graph läuft durch den III und den I Quadranten .
Wertemenge
Gib die Wertemenge der Funktion an.
Es gibt keine Definitionslücken, weshalb man für x jeden Wert einsetzen kann. Das Ergebnis kann jede positive oder negative Zahl sein. Deshalb sind in der Wertemenge alle Zahlen enthalten.
For this task you need the following basic knowledge: Potenzfunktion
Verlauf des Graphen
Überprüfe durch welche Quadranten der Graph verläuft, indem du einen -Wert über 0 und einen unter 0 einsetzt.
Der Graph läuft durch den III. und IV. Quadranten.
Bemerkung: Das ist natürlich ein schrecklich ungenaues Verfahren.
Besser man sagt, dass nie negativ ist und daher nie posiitiv ist. Wegen des Definitionsbereichs muss der Graph dann durch den III. und IV. Quadranten laufen.
Wertemenge
Bestimme die Wertemenge:
Es gibt keine Definitionslücken, weshalb man für x jeden Wert einsetzen kann. Die Ergebnisse können aber nur negative Werte oder sein. Deshalb sind in der Wertemenge alle negativen Werte und die enthalten.
Grad
Lese den Grad der Potenzfunktion ab.
For this task you need the following basic knowledge: Potenzfunktion
Symmetrie
Verlauf des Graphen
Überprüfe durch welche Quadranten der Graph läuft, indem du einen x-Wert unter 0 und einen über 0 einsetzt.
Der Graph verläuft durch den II und den IV Quadranten.
Wertemenge
Bestimme die Wertmenge der Funktion:
Es gibt keine Definitionslücken ,weshalb man für x jeden Wert einsetzen kann. Das Ergebnis kann jede positive oder negative Zahl sein. Deshalb sind in der Wertemenge alle Zahlen enthalten.
Grad
Lese den Grad der Potenzfunktion ab.
f(x) = -1500x=-1500x^\textcolor{ff6600}{1} \Rightarrow \textcolor{ff6600}{n=1} ParseError: Got function '\textcolor' with no arguments as superscript at position 24: … -1500x=-1500x^\̲t̲e̲x̲t̲c̲o̲l̲o̲r̲{ff6600}{1} \Ri…
For this task you need the following basic knowledge: Potenzfunktion
Somit ist der Graph achsensymmetrisch bezüglich der -Achse .
Allgemein sind alle geraden Potenzfunktionen achsensymmetrisch zur -Achse.
Verlauf des Graphen
Überprüfe, durch welche Quadranten der Graph läuft, indem du einen Wert unter und einen über einsetzt.
Der Graph verläuft durch den II. und I. Quadranten (oberhalb der -Achse).
Wertemenge
Bestimme die Wertemenge der Funktion:
Es gibt keine Definitionslücke, also kann man jeden Wert für einsetzen. Das Ergebnis kann aber aufgrund des Exponenten nicht negativ sein. Also sind in der Wertemenge alle positiven Werte und die enthalten.
Grad
Lies den Grad der Potenzfunktion ab:
For this task you need the following basic knowledge: Potenzfunktion
Hinweis: kann man auch als auffassen . Somit ist tatsächlich eine Potenzfunktion.
Symmetrie
Der Graph hat für jeden -Wert den -Wert . Er verläuft also parallel zur -Achse.
Der Graph ist achsensymmetrisch zur -Achse.
Verlauf des Graphen
Überprüfe, durch welche Quadranten der Graph läuft, indem du einen -Wert unter und einen über einsetzt.
Der Graph verläuft durch den II. und I. Quadranten (oberhalb der x-Achse).
Wertemenge
Bestimme die Wertemenge der Funktion.
Nur der Wert gehört zu der Wertemenge dieser Funktion.
Grad
Gib den Grad der Funktion an.
kommt in der Funktion nicht als Faktor vor. Somit ist der Grad der Potenzfunktion .
For this task you need the following basic knowledge: Potenzfunktion
Der Graph ist punktsymmetrisch zum Koordinatenursprung.
Allgemein sind alle ungeraden Potenzfunktionen punktsymmetrisch zum Ursprung.
Verlauf des Graphen
Überprüfe, durch welche Quadranten der Graph läuft, indem du einen -Wert unter und einen über einsetzt.
Der Graph verläuft durch den II. und IV. Quadranten.
Wertemenge
Bestimme die Wertemenge.
Es gibt keine Definitionslücken, weshalb man für jeden Wert einsetzen kann. Das Ergebnis kann jede positive oder negative Zahl sein. Deshalb sind in der Wertemenge alle Zahlen enthalten.
Grad
Lies den Grad der Potenzfunktion ab.
- 4
Bestimme den Grad folgender Potenzfunktionen, mache eine Aussage über das Symmetrieverhalten, den Verlauf des Graphen und die Wertemenge. Zeichne die Graphen jeweils in ein Koordinatensystem.
For this task you need the following basic knowledge: Potenzfunktion
Lies den Grad der Potenzfunktion ab.
Setz in ein, um die Symmetrie des Graphen zu ermitteln.
Der Graph ist achsensymmetrisch .
Setz einen Wert über 0 und einen unter 0 ein, um den Verlauf des Graphen zu ermitteln.
Der Graph verläuft durch den III und IV Quadranten .
Bestimme die Wertemenge, indem du überprüfst, welche Werte für f(x) möglich sind.
Es gibt keine Definitionslücke. Das Ergebnis der Funktion kann aber nur negativ sein, weil vor dem eine negative Zahl steht.
Zeichne den Graphen. Rechne dazu einige Werte der Funktion aus.
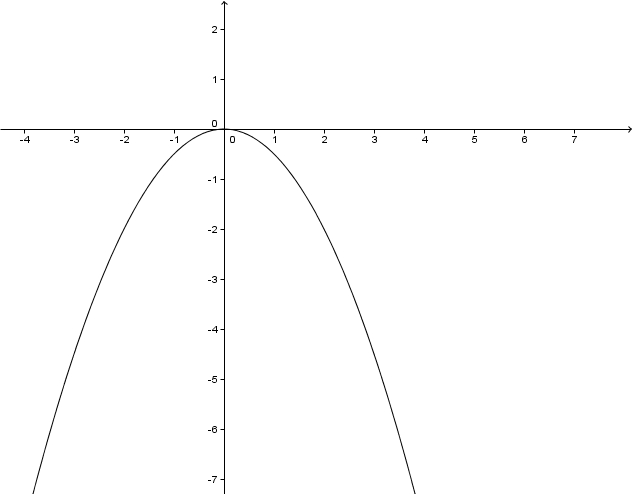
For this task you need the following basic knowledge: Potenzfunktionen
Lies den Grad der Potenfzunktion ab.
Setz in ein , um die Symmetrie des Graphen zu überprüfen.
Der Graph ist punktsymmetrisch .
Überprüfe den Verlauf des Graphen, indem du einen Wert unter 0 und einen über 0 einsetzt.
Der Graph verläuft durch den III und I Quadranten .
Bestimme die Wertemenge, indem du überprüfst welche Werte für f(x) möglich sind.
Die Funktion hat keine Definitionslücke. Es sind positive und negative Werte für f(x) möglich. Das heißt f(x) kann jeden Wert als Ergebnis haben.
Zeichne den Graphen. Rechne dazu einige Werte der Funktion aus.
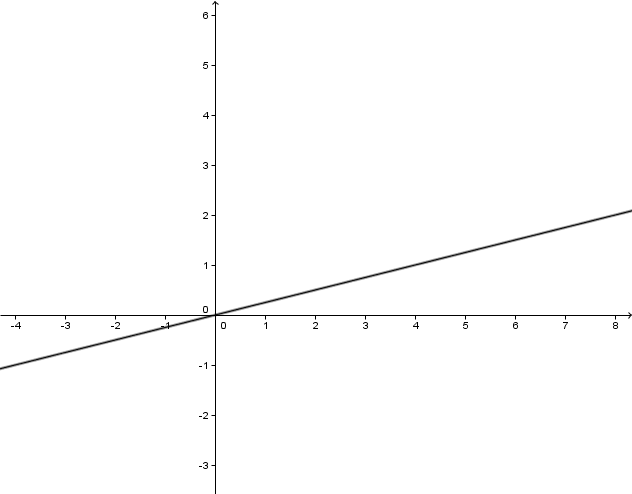
For this task you need the following basic knowledge: Potenzfunktion
Lies den Grad der Potenzfunktion ab.
Setz in ein, um die Symmetrie des Graphen zu überprüfen.
Der Graph der Funktion ist achsensymmetrisch .
Bestimme den Verlauf der Funktion, indem du einen Wert unter 0 und einen über 0 einsetzt.
Der Graph verläuft durch den III und IV Quadranten .
Bestimme die Wertemenge, indem du überprüfst welche Werte für f(x) möglich sind.
Es gibt keine Definitionslücke. Das Ergebnis der Funktion kann aber nur negativ sein, weil bei immer positive Werte entstehen, davor aber steht.
Zeiche den Graphen. Rechne dazu einige Werte der Funktion aus.
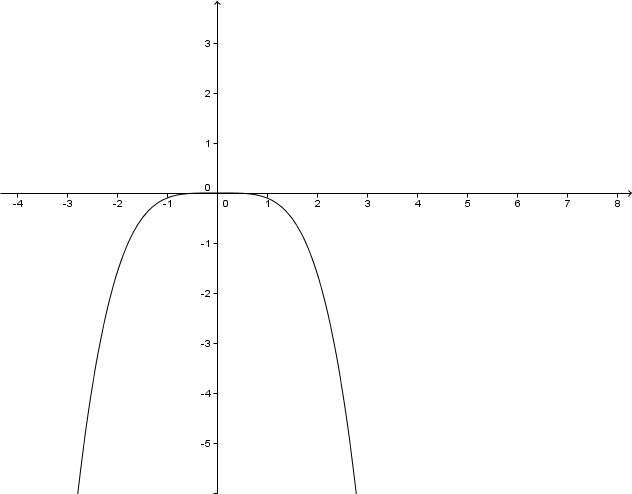
For this task you need the following basic knowledge: Potenzfunktion
Lies den Grad der Potenzfunktion ab.
Setz in ein, um die Symmetrie des Graphen zu überprüfen.
Der Graph ist punktsymmetrisch .
Bestimme den Verlauf der Funktion, indem du einen Wert unter 0 und einen über 0 einsetzt.
Der Graph verläuft durch den III und I Quadranten .
Bestimme die Wertemenge, indem du überprüfst welche Werte für f(x) möglich sind.
Es gibt keine Definitionslücke . Das Ergebnis schließt jeden positiven und negativen Wert mit ein.
Zeichne den Graphen. Rechne dazu einige Werte der Funktion aus.
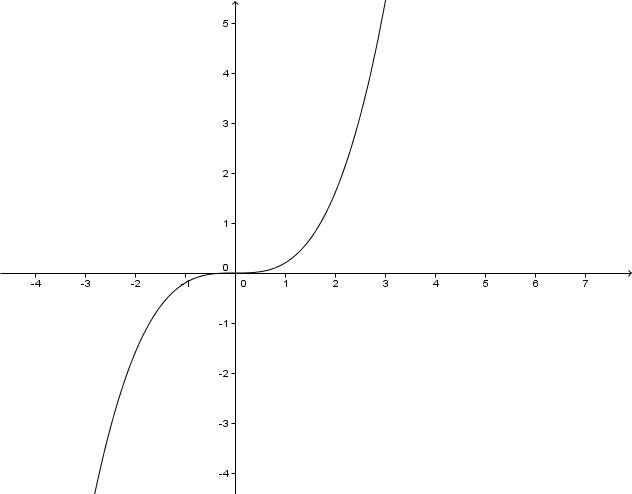
For this task you need the following basic knowledge: Potenzfunktion
Lies den Grad der Potenzfunktion ab.
Setz für ein, um die Symmetrie des Graphen zu überprüfen.
Der Graph ist punktsymmetrisch .
Bestimme den Verlauf der Funktion, indem du einen Wert unter 0 und einen über 0 einsetzt.
Der Graph verläuft durch den III und IV Quadranten.
Bestimme die Wertemenge, indem du überprüfst welche Werte für f(x) möglich sind.
Es gibt keine Definitionslücke Das Ergebnis der Funktion schließt jeden positiven und negativen Wert mit ein.
Zeichne den Graphen. Rechne dazu einige Werte der Funktion aus.
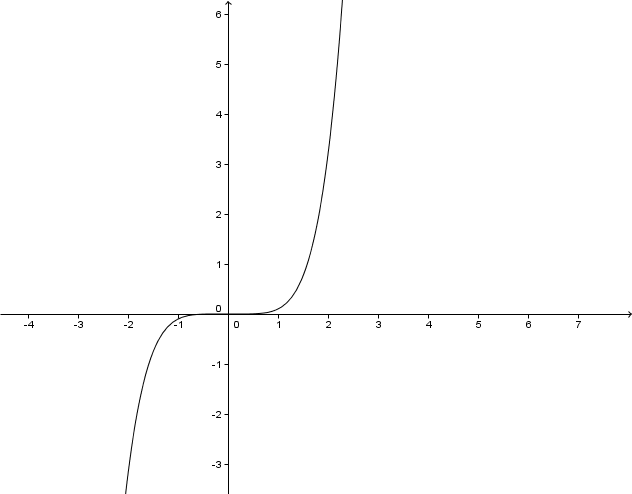
For this task you need the following basic knowledge: Potenzfunktion
Lies den Grad der Potenzfunktion ab.
Setz in ein, um die Symmetrie des Graphen zu überprüfen.
Der Graph ist punktsymmetrisch .
Bestimme den Verlauf der Funktion, indem du einen Wert unter 0 und einen über 0 einsetzt.
Der Graph verläuft durch den II und IV Quadranten .
Bestimme die Wertemenge , indem du überprüfst welche Werte für f(x) möglich sind.
Es gibt keine Definitionslücke . Das Ergebnis der Funktion schließt jeden positiven und negativen Wert mit ein.
Zeichne den Graphen. Rechne dazu einige Werte der Funktion aus.
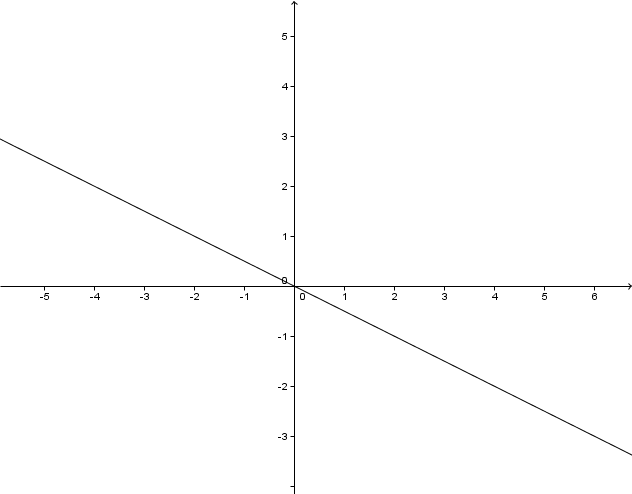
For this task you need the following basic knowledge: Potenzfunktion
Lies den Grad der Potenzfunktion ab.
Setz in ein, um die Symmetrie des Graphen zu überprüfen.
Der Graph ist punktsymmetrisch .
Bestimme den Verlauf der Funktion, indem du einen Wert unter 0 und einen über 0 einsetzt.
Der Graph verläuft durch den II und IV Quadranten .
Bestimme die Wertemenge der Funktion, indem du überprüfst welche Werte für f(x) möglich sind.
Es gibt keine Definitionslücke .Das Ergebnis der Funktion schließt jeden positiven und negativen Wert mit ein.
Zeichne den Graphen. Rechne dazu einige Werte der Funktion aus.
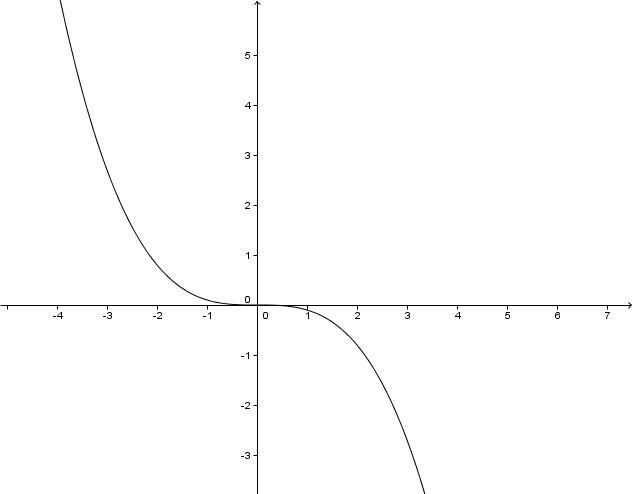
For this task you need the following basic knowledge: Potenzfunktion
Lies den Grad der Potenzfunktion ab.
Setz in ein, um die Symmetrie des Graphen zu überprüfen.
Der Graph ist achsensymmetrisch .
Bestimme den Verlauf der Funktion, indem du einen Wert unter 0 und einen über 0 einsetzt.
Der Graph verläuft durch den II und I Quadranten .
Bestimme die Wertemenge , indem du überprüfst welche Werte für f(x) möglich sind.
Der Graph hat keine Definitionslücke . Aufgrund des , das vorkommt sind aber nur positive Werte als Ergebnis möglich.
Zeichne den Graphen. Rechne dazu einige Werte der Funktion aus.
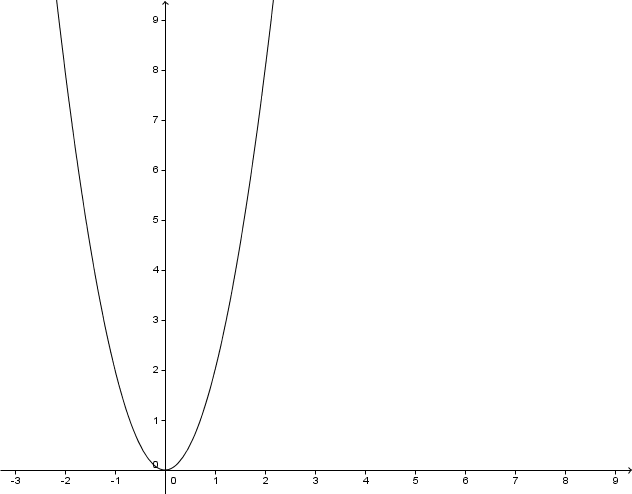
For this task you need the following basic knowledge: Potenzfunktion
Lies den Grad der Potenzfunktion ab.
Setz in ein, um die Symmetrie des Graphen zu überprüfen.
Der Graph ist achsensymmetrisch .
Bestimme den Verlauf der Funktion, indem du einen Wert unter 0 und einen über 0 einsetzt.
Der Graph verläuft durch den II und I Quadranten .
Bestimme die Wertemenge , indem du überprüfst welche Werte für f(x) möglich sind.
Der Graph hat keine Definitionslücke. Aufgrund des . das vorkommt sind aber nur positive Werte als Ergebnis möglich.
Zeichne den Graphen. Rechne dazu einige Werte der Funktion aus.
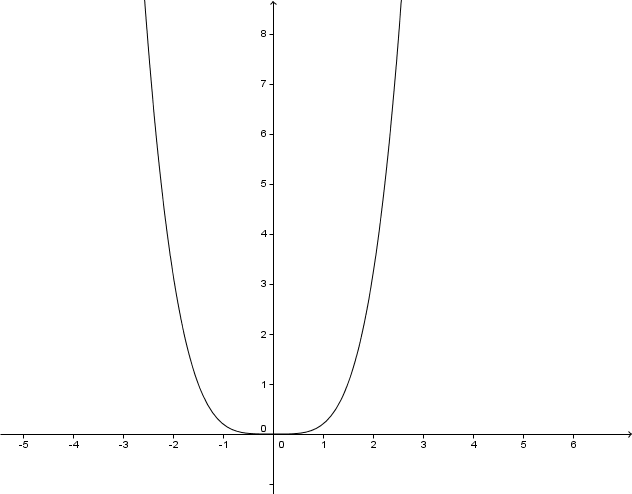
For this task you need the following basic knowledge: Potenzfunktion
Lies den Grad der Potenzfunktion ab.
Setz in ein, um die Symmetrie des Graphen zu überprüfen.
Der Graph ist achsensymmetrisch .
Bestimme den Verlauf der Funktion, indem du einen Wert unter 0 und einen über 0 einsetzt.
Der Graph verläuft durch den III und IV Quadranten .
Bestimme die Wertemenge , indem du überprüfst welche Werte für f(x) möglich sind.
Der Graph hat keine Definitionslücke . Aufgrund der negativen Zahl vor dem , sind nur negative Ergebnisse möglich,.
Zeichne den Graphen. Rechne dazu einige Werte der Funktion aus..
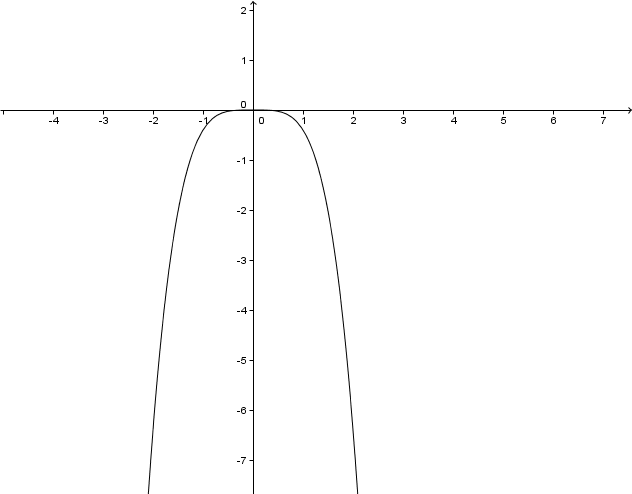
- 5
Der Graph der Potenzfunktion vierten Grades soll um 3 Einheiten nach rechts verschoben und anschließend um den Faktor 2 gestreckt werden.
a. Gib die Funktionsgleichung für den verschobenen Graphen an.
b. Weise nach, dass der Graph weder zur y-Achse noch zum Ursprung symmetrisch ist.
For this task you need the following basic knowledge: Funktionsgleichung aufstellen
Ausgangsfunktion:
Um den Graph 3 nach rechts zu verschieben muss vom -Wert 3 subtrahiert werden und das Ergebnis dann hoch 4 genommen werden.
Um den Graphen mit dem Faktor 2 in -Richtung zu strecken muss die Funktion mit 2 multiplizert werden.
Symmetrie
Da f eine gerade Potenzfunktion ist, liegt sie symmetrisch zur -Achse. Durch eine Verschiebung um 3 nach rechts, lautet die Symmetrieachse von g bzw. h jetzt x =3 und ist parallel zur -Achse.
Eine ganzrationale Funktion vom Grad 4 kann niemals punktsymmetrisch sein.
- 6
Gib jeweils den Definitionsbereich für die Wurzelfunktion an.
For this task you need the following basic knowledge: Definititonsbereich
Der Definitionsbereich einer Funktion umfasst die Menge der Zahlen, die in die Funktion eingesetzt werden dürfen.
Unter geraden Wurzeln darf kein negativer Radikand stehen, d.h. der Radikand muss größer oder gleich null sein.
Prüfe, wann der Radikand größer oder gleich null ist.
↓ Löse nach auf.
oder
For this task you need the following basic knowledge: Definititonsbereich
Der Definitionsbereich einer Funktion umfasst die Menge der Zahlen, die in die Funktion eingesetzt werden dürfen.
Unter geraden Wurzeln darf kein negativer Radikand stehen, d.h. der Radikand muss größer oder gleich null sein.
Prüfe, wann der Radikand größer oder gleich null ist.
Alle Zahlen, für die ist, gehören nicht zum Definitionsbereich:
oder
Alle Zahlen, für die ist, gehören zum Definitionsbereich:
For this task you need the following basic knowledge: Definititonsbereich
Der Definitionsbereich einer Funktion umfasst die Menge der Zahlen, die in die Funktion eingesetzt werden dürfen.
Unter geraden Wurzeln darf kein negativer Radikand stehen, d.h. der Radikand muss größer oder gleich null sein.
Prüfe, wann der Radikand größer oder gleich null ist.
Der Radikand ist für alle immer größer als null.
Der Definitionsbereich der Funktion muss nicht eingeschränkt werden.
- 7
Gegeben sind die beiden Wurzelfunktionen und .
Bestimme für beide Funktionen jeweils den maximalen Definitionsbereich.
For this task you need the following basic knowledge: Definitionsbereich
Der Definitionsbereich einer Funktion umfasst die Menge der Zahlen, die in die Funktion eingesetzt werden dürfen.
Unter geraden Wurzeln darf kein negativer Radikand stehen, d.h. der Radikand muss größer oder gleich null sein.
Funktion f(x)
Prüfe, wann der Radikand größer oder gleich null ist.
↓ Löse nach auf.
Damit hat die Funktion den Definitionsbereich
Funktion g(x)
Prüfe, wann der Radikand größer oder gleich null ist.
↓ Löse nach auf.
Damit hat die Funktion den Definitionsbereich
Gib für beide Funktionen jeweils die Schnittpunkte mit den Koordinatenachsen an.
For this task you need the following basic knowledge: Schnittpunkte mit den Koordinatenachsen
Funktion f(x)
Schnittpunkt mit der -Achse: Setze :
↓ Löse nach auf.
Die Funktion schneidet die -Achse im Punkt .
Schnittpunkt mit der -Achse: Setze ein:
↓ Setze ein.
↓ Ziehe die Wurzel.
Die Funktion schneidet die -Achse im Punkt .
Funktion g(x)
Schnittpunkt mit der -Achse: Setze :
↓ Löse nach auf.
Die Funktion schneidet die -Achse im Punkt .
Schnittpunkt mit der -Achse: Setze ein:
↓ Setze ein.
↓ Ziehe die Wurzel.
Die Funktion schneidet die -Achse im Punkt .
Zeichne beide Graphen für in ein Koordinatensystem ein. Rechne dazu einige Funktionswerte aus.
For this task you need the following basic knowledge: Koordinatensystem
Für beide Funktionen werden einige Funktionswerte berechnet.
0
In welchem Punkt schneiden sich die Graphen von und ?
For this task you need the following basic knowledge: Schnittpunkt zweier Funktionen
Setze :
↓ Löse nach auf.
↓ Kürze
Du hast die Lösung erhalten. Bei der Berechnung dieser Lösung wurde quadriert. Da das Quadrieren keine Äquivalenzumformung ist, muss geprüft werden, ob im gemeinsamen Definitionsbereich der beiden Funktionen liegt.
Außerdem ist eine Probe erforderlich.
Der gemeinsame Definitionsbereich der beiden Funktionen lautet:
. Die Lösung ist in diesem Definitionsbereich enthalten.
Mache nun eine Probe:
Setze in die Wurzelgleichung ein:
↓ Vereinfache.
↓ Fasse zusammen.
Mit der Probe für hast du gleichzeitig den -Wert des Schnittpunkts berechnet:
Antwort: Der Schnittpunkt der beiden Funktionen hat die Koordinaten .
Hinweis: Der Schnittpunkt ist in der Abbildung zu Aufgabe c) eingezeichnet.
Beide Funktionen werden um nach rechts verschoben und mit dem Faktor gestreckt. Wie heißen die neuen Funktionsgleichungen und ?
For this task you need the following basic knowledge: Funktionsgraphen stauchen und strecken
Die Funktion wird um nach rechts verschoben:
und anschließend mit dem Faktor gestreckt:
Die Funktion wird um nach rechts verschoben:
und anschließend mit dem Faktor gestreckt:
- 8
Gegeben ist die Funktion .
Bestimme den maximalen Definitionsbereich.
For this task you need the following basic knowledge: Definitionsbereich
Der Definitionsbereich einer Funktion umfasst die Menge der Zahlen, die in die Funktion eingesetzt werden dürfen.
Unter geraden Wurzeln darf kein negativer Radikand stehen, d.h. der Radikand muss größer oder gleich null sein.
Beide Wurzeln im Funktionsterm müssen untersucht werden:
Wurzelterm 1:
Prüfe, wann der Radikand größer oder gleich null ist.
Wurzelterm 2:
Prüfe, wann der Radikand größer oder gleich null ist.
Damit hat die Funktion den maximalen Definitionsbereich:
(Mit ist die Bedingung für den . Wurzelterm auch erfüllt.)
Zeichne mithilfe einer Wertetabelle den Graphen der Funktion für
For this task you need the following basic knowledge: Wertetabelle
Für die Wertetabelle werden einige Funktionswerte berechnet.
Beginne mit dem linken Rand des Definitionsbereiches mit .
(gerundete Werte)
Graphische Darstellung:
Berechne den Schnittpunkt mit der -Achse.
Tipp: Es muss zweimal quadriert werden.
For this task you need the following basic knowledge: Nullstelle
Die -Achse wird geschnitten, wenn ist.
Setze .
↓ Beseitige die Wurzeln durch Quadrieren, beachte die binomische Formel.
↓ Fasse zusammen.
↓ Der Wurzelterm muss allein auf einer Seite stehen.
Du hast wieder eine Wurzelgleichung erhalten. d.h. es muss erneut quadriert werden.
↓ Beseitige die Wurzel durch Quadrieren.
↓ Vereinfache. Beachte die binomische Formel auf der rechten Seite.
↓ Fasse zusammen und löse die Klammer auf.
↓ Bringe alle Terme auf eine Seite.
Du hast die quadratische Gleichung erhalten. Diese kannst du nun mit der Mitternachtsformel (abc-Formel) oder mit der p-q-Formel lösen. Hier erfolgt die Lösung mit der p-q-Formel.
Lies die Werte für und ab:
und
Setze die Werte in die p-q-Formel ein:
↓ Setze und ein.
↓ Vereinfache.
Du hast die Lösungen und erhalten. Bei der Berechnung dieser Lösungen wurde quadriert. Da das Quadrieren keine Äquivalenzumformung ist, muss geprüft werden, welche der beiden Lösungen die gesuchte Lösung der Gleichung ist.
Probe mit :
Setze in ein:
↓ Vereinfache.
↓ Ziehe die Wurzeln.
↓ Fasse zusammen.
und somit ist keine Lösung der Wurzelgleichung und somit auch keine Nullstelle.
Probe mit :
Setze in ein:
↓ Vereinfache.
↓ Ziehe die Wurzeln.
↓ Fasse zusammen.
und somit ist die Lösung der Wurzelgleichung und damit die gesuchte Nullstelle.
Antwort: Der Schnittpunkt mit der -Achse lautet: .
- 9
Der Marineclub hat als Logo einen stilisierten Fisch (siehe Abbildung).
Das Logo wird durch die beiden Randfunktionen und modelliert. Dabei ist die untere Randfunktion gegeben durch .
Wie lautet die Funktionsgleichung von ?
For this task you need the following basic knowledge: Spiegelung einer Funktion
Wird die Funktion an der -Achse gespiegelt, erhältst du die Funktion .
Für die Spiegelung an der -Achse muss der Funktionsterm von mit multipliziert werden. Damit hat die Funktion die Funktionsgleichung:
Berechne die Nullstellen von und skaliere die Koordinatenachsen in der Abbildung.
For this task you need the following basic knowledge: Nullstelle
Nullstellenberechnung
Setze :
Du hast die Gleichung erhalten, die du mit dem Satz vom Nullprodukt lösen kannst. Die Nullproduktregel sagt aus, wenn das Produkt von und gleich ist, so ist oder .
↓ Quadriere.
Somit ist und/oder .
Antwort: Die beiden Nullstellen der Funktion sind und .
Skalierung der Koordinatenachsen
Skalierung der -Achse
Die beiden Nullstellen werden in das Koordinatensystem der obigen Abbildung eingetragen und geben die Skalierung der -Achse vor.
Die beiden Nullstellen sind und . Das Intervall auf der -Achse ist in zwei Abschnitte unterteilt, d.h. ein Abschnitt entspricht einer Einheit.
Damit kann die -Achse skaliert werden.
Skalierung der -Achse
Für die Skalierung der -Achse kann z.B. berechnet werden.
Setze in ein:
Die Funktion hat für etwa den Funktionswert .
Damit kann auch die -Achse skaliert werden.
Bestimme den Definitionsbereich der Funktion .
For this task you need the following basic knowledge: Definitionsbereich
Die Funktion ist von (Nullstelle ) bis gezeichnet. Der Definitionsbereich ist somit:
- 10
Gegeben sind die beiden Funktionen und .
Berechne, in welchem Punkt sich die beiden Funktionsgraphen schneiden.
Für die Schnittpunktberechnung setze . Du erhältst eine Wurzelgleichung .
1. Bestimme den Definitionsbereich für die Wurzeln
ist für nicht definiert, d.h. für .
Somit ergibt sich der Definitionsbereich für diese Wurzel:
ist für nicht definiert, d.h. für .
Der Definitionsbereich für diese Wurzel ist dann:
Der gemeinsame Gültigkeitsbereich für die zwei Wurzeln kann an der Zahlengeraden veranschaulicht werden. Der Bereich, indem sich die zwei Strahlen überschneiden, ist der Definitionsbereich (Gültigkeitsbereich) für die Wurzelgleichung.
Ab überschneiden sich die beiden Gültigkeitsbereiche für die Wurzeln.
Für die Wurzelgleichung gilt dann:
Alle Umformungen erfolgen nun unter der allgemeinen Annahme, dass ist.
2. Beseitigung der Wurzeln durch Quadrieren
↓ Beseitige die Wurzel durch Quadrieren.
↓ Löse nach auf.
liegt im Definitionsbereich der Wurzelgleichung.
3. Probe für die erhaltene Lösung durchführen
Probe für :
Setze in die Wurzelgleichung ein:
↓ Vereinfache.
↓ Ziehe die Wurzel.
Mit der Probe für hast du gleichzeitig den -Wert des Schnittpunkts berechnet:
Die beiden Graphen schneiden sich im Punkt .
Zeichne die beiden Graphen mithilfe einer Wertetabelle.
Berechne einige Funktionswerte der beiden Graphen:
mit
Beispielsweise ist
Setzt man hingegen in ein, so ergibt sich . Der Radikand ist negativ und die Wurzel ist nicht definiert. Beachte den Definitionsbereich für g(x):
nicht definiert
nicht definiert
nicht definiert
nicht definiert
4
4
Graphische Darstellung





